 福岡大学附属大濠高等学校
福岡大学附属大濠高等学校
 福岡大学附属大濠高等学校
福岡大学附属大濠高等学校
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
この動画を見る
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
【見た目より難しい…!】連立方程式:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+4y=23\\
2x-6y=-15
\end{array}
\right.
\end{eqnarray}\;$を解け。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+4y=23\\
2x-6y=-15
\end{array}
\right.
\end{eqnarray}\;$を解け。
【分かりやすく順を追って…!】整数:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
正の整数$m,n$:$1 \lt \sqrt{m} \lt 2, 5 \lt \sqrt{n} \lt 6$のとき、$m+n$で作られる素数は何通りか求めよ。
この動画を見る
正の整数$m,n$:$1 \lt \sqrt{m} \lt 2, 5 \lt \sqrt{n} \lt 6$のとき、$m+n$で作られる素数は何通りか求めよ。
【案外戸惑う…!】整数:福岡大学付属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
この動画を見る
直線$ y=-\dfrac{1}{2}x+10 $上の点で
$ x $座標も$ y $座標も正の整数である点は全部で$ \Box $個ある.
福岡大学付属大濠高等学校過去問
【学問に王道なし!】整数:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
【ルールを抑えるのが大切!】文字式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
【3分で確認、計算のルール!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$(\displaystyle \frac{6}{\sqrt{ 3 }}-\sqrt{ 18 })(\sqrt{ 12 }+\displaystyle \frac{6}{\sqrt{ 2 }})$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$(\displaystyle \frac{6}{\sqrt{ 3 }}-\sqrt{ 18 })(\sqrt{ 12 }+\displaystyle \frac{6}{\sqrt{ 2 }})$
を計算し、簡単にすると▬である。
【まず3分!身に付く解法!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$\{ (2+\sqrt{ 5 })^2+(2-\sqrt{ 5 })^2\}^2-\{ (2+\sqrt{ 5 })^2-(2-\sqrt{ 5 })^2\}^2$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$\{ (2+\sqrt{ 5 })^2+(2-\sqrt{ 5 })^2\}^2-\{ (2+\sqrt{ 5 })^2-(2-\sqrt{ 5 })^2\}^2$
を計算し、簡単にすると▬である。
【3分で基礎力アップ!】平方根:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#平方根#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
$\displaystyle \frac{(\sqrt{ 3 }+2)(3+\sqrt{ 3 })(9-5\sqrt{ 3 })}{\sqrt{ 3 }}$
を計算し、簡単にすると▬である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
$\displaystyle \frac{(\sqrt{ 3 }+2)(3+\sqrt{ 3 })(9-5\sqrt{ 3 })}{\sqrt{ 3 }}$
を計算し、簡単にすると▬である。
【5分で完全理解!】図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
▭部分を求めよ。
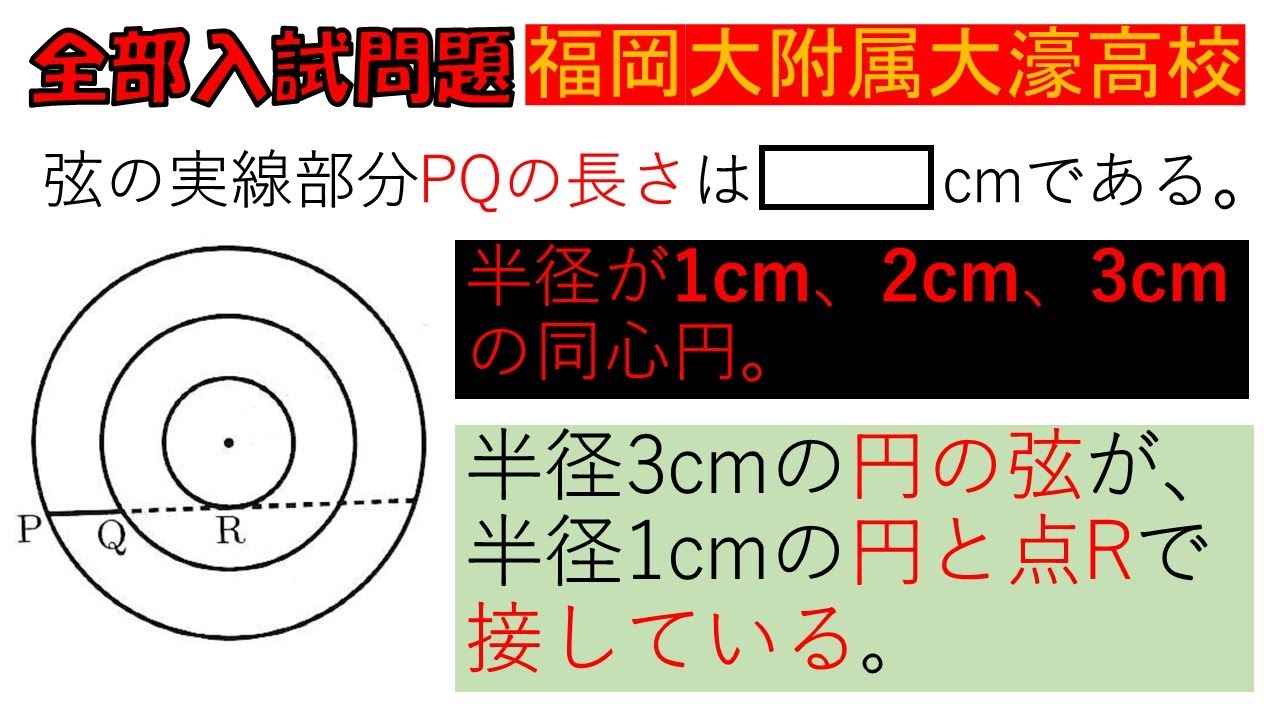
弦の実線部分$PQ$の長さは▭cmである。
半径が1cm、2cm、3cm の同心円。
半径3cmの円の弦が、 半径1cmの円と点$R$で 接している。
※図は動画内参照
この動画を見る
入試問題 福岡大学附属大濠高等学校
▭部分を求めよ。
弦の実線部分$PQ$の長さは▭cmである。
半径が1cm、2cm、3cm の同心円。
半径3cmの円の弦が、 半径1cmの円と点$R$で 接している。
※図は動画内参照
図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
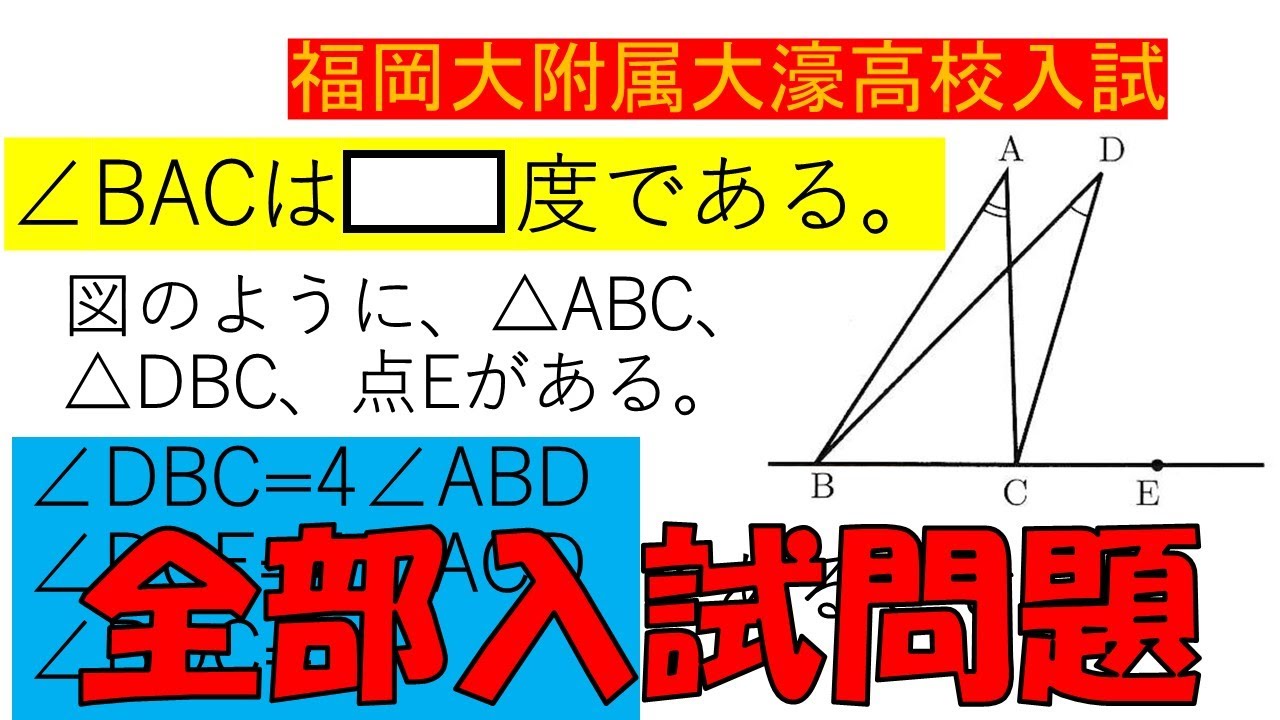
図のように、$\triangle ABC$、 $\triangle DBC$、点$E$がある。
$\angle DBC=4 \angle ABD$
$\angle DCE=4 \angle ACD$
$\angle BDC28^{ \circ }$
であるとき$\angle BAC$は▭度である。
▭部分を答えよ。
この動画を見る
入試問題 福岡大学附属大濠高等学校
図のように、$\triangle ABC$、 $\triangle DBC$、点$E$がある。
$\angle DBC=4 \angle ABD$
$\angle DCE=4 \angle ACD$
$\angle BDC28^{ \circ }$
であるとき$\angle BAC$は▭度である。
▭部分を答えよ。
因数分解:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
この動画を見る
入試問題 福岡大学附属大濠高等学校
次の問いに答えよ。
$x^2y^2-4x^2-9y^2+36$
を因数分解すると▭である。
【得意な解法を身に付けたい!】二次方程式:福岡大学付属大濠高等学校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 福岡大学付属大濠高等学校
次の問いに答えよ。
$x^2+ax-b=0$の$2$解が
$x^2+6x-5=0$の$2$解より
それぞれ$2$だけ大きい
定数$a, b$の値は$口$である。
この動画を見る
入試問題 福岡大学付属大濠高等学校
次の問いに答えよ。
$x^2+ax-b=0$の$2$解が
$x^2+6x-5=0$の$2$解より
それぞれ$2$だけ大きい
定数$a, b$の値は$口$である。
