 慶應義塾高等学校
慶應義塾高等学校
 慶應義塾高等学校
慶應義塾高等学校
calculation : Shirotan's cute kawaii math show #数学 #高校入試 #京大数学 #小学生テスト

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(30²+37²+44²+…+79²)-(1²+8²+15²+…+50²)=?
この動画を見る
(30²+37²+44²+…+79²)-(1²+8²+15²+…+50²)=?
【ストーリーを読め…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#数A#高校入試過去問(数学)#数学(高校生)#慶應義塾高等学校
指導講師:
問題文全文(内容文):
$x^2 + (3y - 9)x + y(2y - 9)が素数の平方数となるような$
$9以下の正の整数x,yの組を全て求めよ$
この動画を見る
$x^2 + (3y - 9)x + y(2y - 9)が素数の平方数となるような$
$9以下の正の整数x,yの組を全て求めよ$
【ひらめきと経験と…!】図形:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
この動画を見る
$\triangle ABCにおいて、AB=AC,BC=2,\angle BAC=36^{ \circ }$
$のとき、ABの長さを求めよ。$
【初見では固まる…!】平方根:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$
この動画を見る
$次の式を計算せよ。$
$\dfrac{1}{(1+\sqrt{2}+\sqrt{3})^2}+\dfrac{1}{(1+\sqrt{2}-\sqrt{3})^2}$
【どれも大切…!】二次方程式:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
この動画を見る
$2x^2+10\sqrt{2}x+9=0$の解を求めよ。
【分かったつもりでは…!】連立方程式:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{1}
\frac{5}{x-\sqrt{2}}+\frac{2}{x+\sqrt{2}y}=1\\
\frac{1}{x-\sqrt{2}}-\frac{5}{x+\sqrt{2}y}=2
\end{array}
\right.
\end{eqnarray}
の解を求めよ。
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{1}
\frac{5}{x-\sqrt{2}}+\frac{2}{x+\sqrt{2}y}=1\\
\frac{1}{x-\sqrt{2}}-\frac{5}{x+\sqrt{2}y}=2
\end{array}
\right.
\end{eqnarray}
の解を求めよ。
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法
単元:
#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
この動画を見る
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
この動画を見る
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
【正体見たり…!】平方根:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
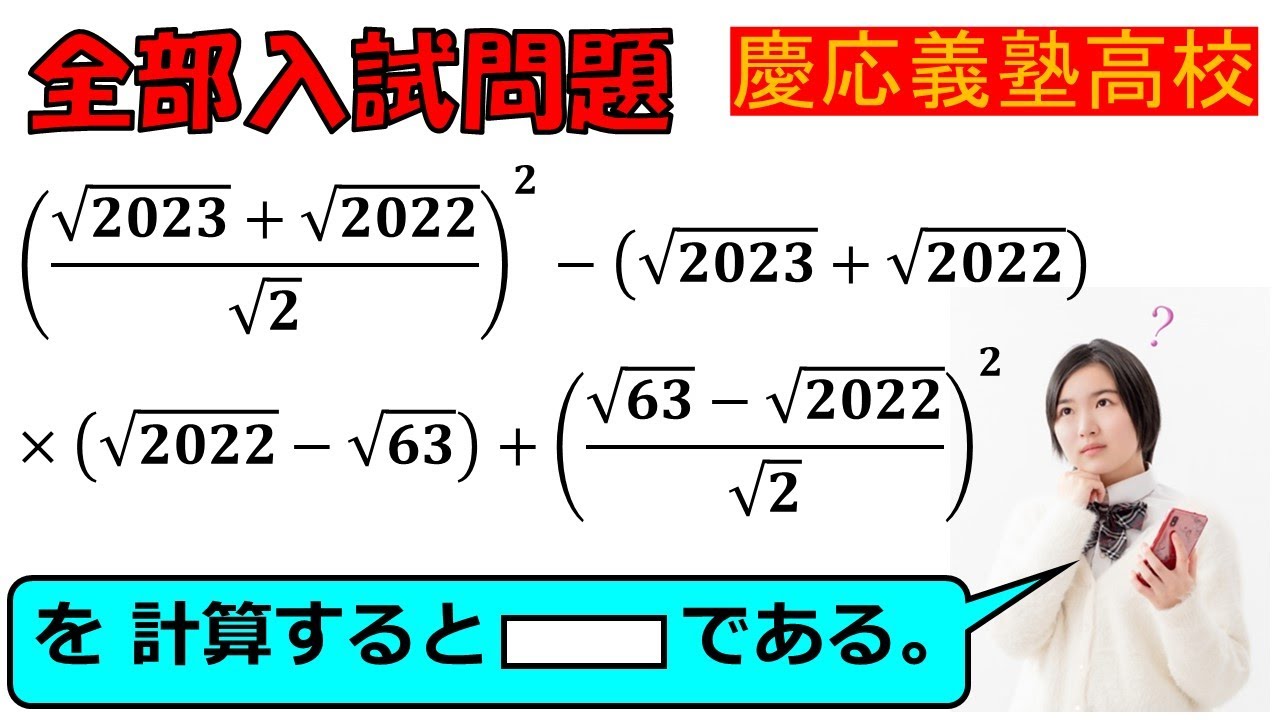
入試問題 慶応義塾高等学校
$(\displaystyle \frac{\sqrt{ 2023 }+\sqrt{ 2022 }}{\sqrt{ 2 }})^2-(\sqrt{ 2023 }+\sqrt{ 2022 }) \times (\sqrt{ 2022 }-\sqrt{ 63 })+(\displaystyle \frac{\sqrt{ 63 }-\sqrt{ 2022 }}{\sqrt{ 2 }})^2$
を計算すると▭である。
この動画を見る
入試問題 慶応義塾高等学校
$(\displaystyle \frac{\sqrt{ 2023 }+\sqrt{ 2022 }}{\sqrt{ 2 }})^2-(\sqrt{ 2023 }+\sqrt{ 2022 }) \times (\sqrt{ 2022 }-\sqrt{ 63 })+(\displaystyle \frac{\sqrt{ 63 }-\sqrt{ 2022 }}{\sqrt{ 2 }})^2$
を計算すると▭である。
🍭【峠を越えれば…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
この動画を見る
$ 7^{123}$を$100$で割ると,余りは$ \Box $である.
次の空欄をうめよ.
慶應義塾高校過去問
【挑戦しよう!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
この動画を見る
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
【やることは分かってる!?】有理数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{3007}{3201}$を既約分数に直すと$ \Box $である.
慶應義塾高校過去問
この動画を見る
$ \dfrac{3007}{3201}$を既約分数に直すと$ \Box $である.
慶應義塾高校過去問
【まずは完答、それから本質をつかむこと!】図形:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
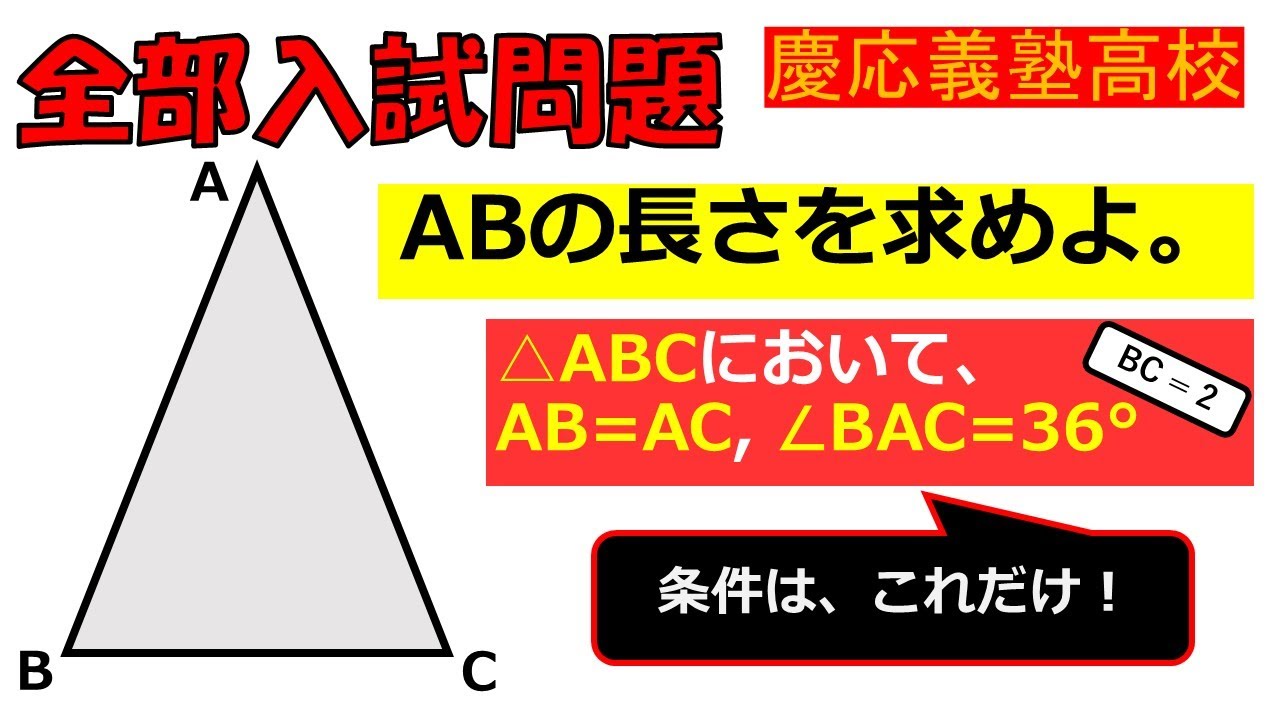
$ \triangle ABC$において,$\angle BAC=36^{ \circ }$
$BC=2$
条件はこれだけ!
※図は動画内参照
この動画を見る
$ \triangle ABC$において,$\angle BAC=36^{ \circ }$
$BC=2$
条件はこれだけ!
※図は動画内参照
【連立方程式最終問題⁈】連立方程式:慶応義塾高等学校(訂正版)~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#平方根#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
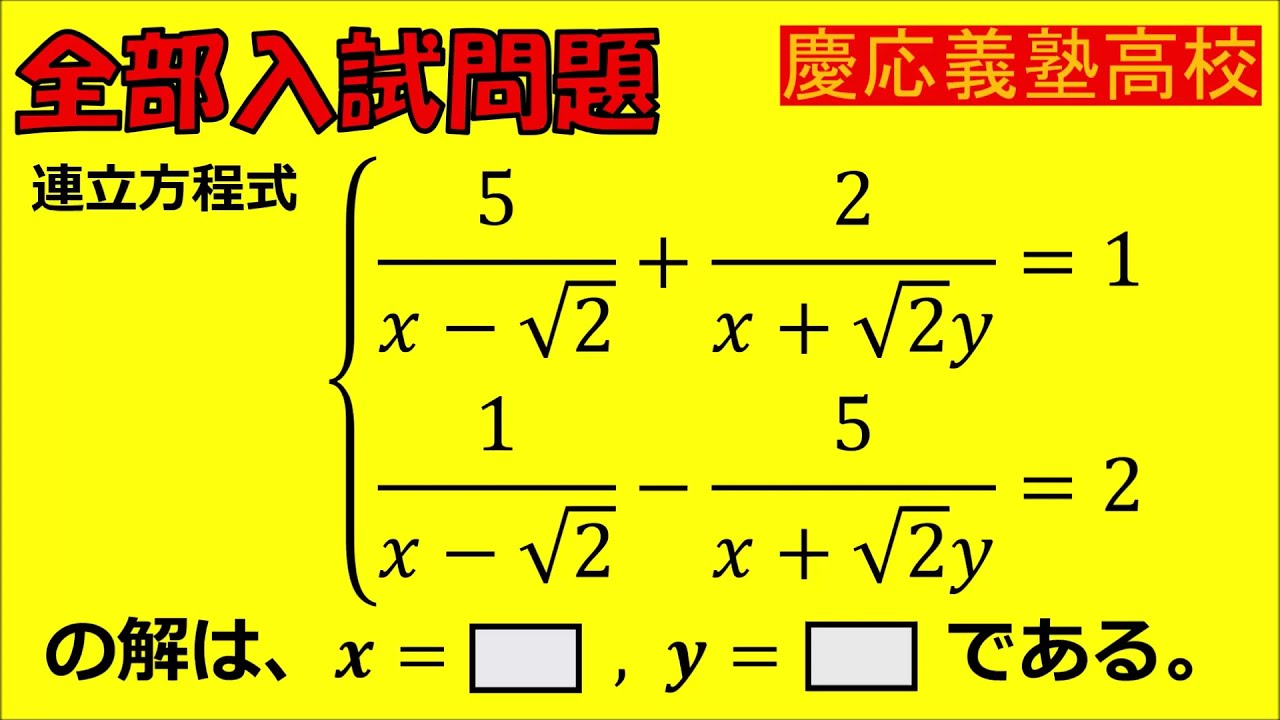
入試問題 慶応義塾高等学校
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{5}{x-\sqrt{ 2 }} + \displaystyle \frac{2}{x+\sqrt{ 2 y}}= 1 \\
\displaystyle \frac{1}{x-\sqrt{ 2 }} - \displaystyle \frac{5}{x+\sqrt{ 2y }} = 2
\end{array}
\right.
\end{eqnarray}$
の解は、$x=$▭、$y=$▭である。
四角部分を求めよ。
この動画を見る
入試問題 慶応義塾高等学校
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{5}{x-\sqrt{ 2 }} + \displaystyle \frac{2}{x+\sqrt{ 2 y}}= 1 \\
\displaystyle \frac{1}{x-\sqrt{ 2 }} - \displaystyle \frac{5}{x+\sqrt{ 2y }} = 2
\end{array}
\right.
\end{eqnarray}$
の解は、$x=$▭、$y=$▭である。
四角部分を求めよ。
【人生が変わる⁉】因数分解:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
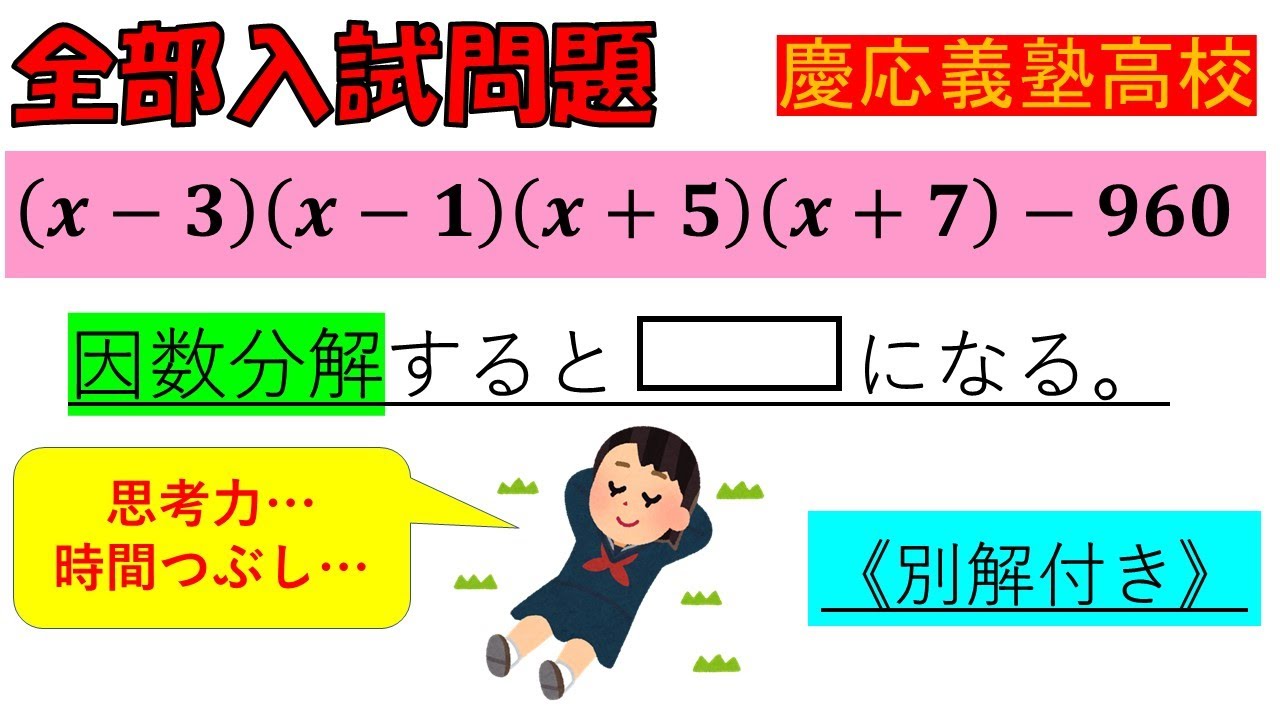
入試問題 慶応義塾高等学校
$(x-3)(x-1)(x+5)(x+7)-960$
因数分解すると▭になる。
この動画を見る
入試問題 慶応義塾高等学校
$(x-3)(x-1)(x+5)(x+7)-960$
因数分解すると▭になる。
文字式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応義塾高等学校
次の空欄をうめよ。
$3x^2 - 15x +7=0$ のとき
→$3x^4 – 15x^3 + 35x – 16 $
の値は▭である。
この動画を見る
入試問題 慶応義塾高等学校
次の空欄をうめよ。
$3x^2 - 15x +7=0$ のとき
→$3x^4 – 15x^3 + 35x – 16 $
の値は▭である。
