 立教新座高等学校
立教新座高等学校
 立教新座高等学校
立教新座高等学校
2つの二次方程式 2025立教新座

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
この動画を見る
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
【効率…良く…!】文字式:立教新座高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#平方根#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2\sqrt{3}a+\sqrt{3}b=5\\
\sqrt{3}a+2\sqrt{3}b=-3
\end{array}
\right.
\end{eqnarray}\;$のとき、
$a+b$の値を求めなさい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2\sqrt{3}a+\sqrt{3}b=5\\
\sqrt{3}a+2\sqrt{3}b=-3
\end{array}
\right.
\end{eqnarray}\;$のとき、
$a+b$の値を求めなさい。
円と接線と三角形 立教新座
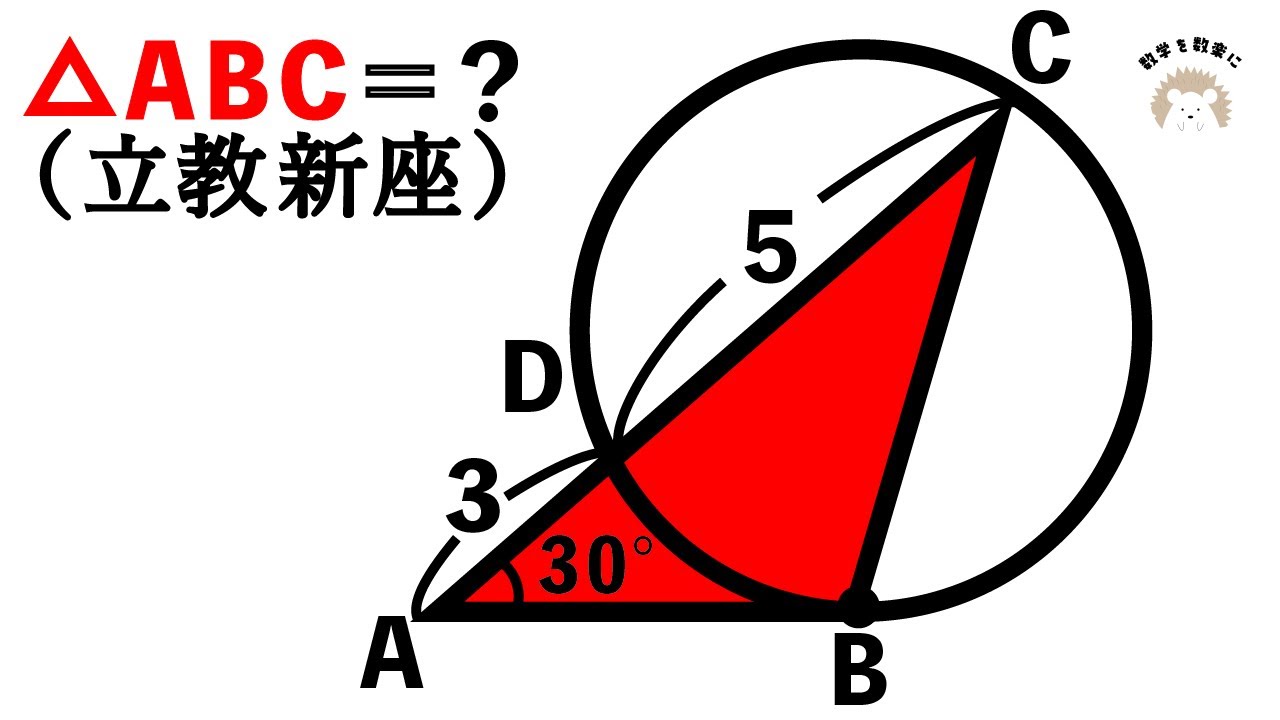
円と接線と三角形 立教新座

integer problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\displaystyle \frac{24}{a^2+4a+3}\;$が自然数となるような整数$a\;$は何個ありますか。
※$a^2+4a+3\;$は0ではない。
この動画を見る
$\displaystyle \frac{24}{a^2+4a+3}\;$が自然数となるような整数$a\;$は何個ありますか。
※$a^2+4a+3\;$は0ではない。
平方根 式の値 立教新座
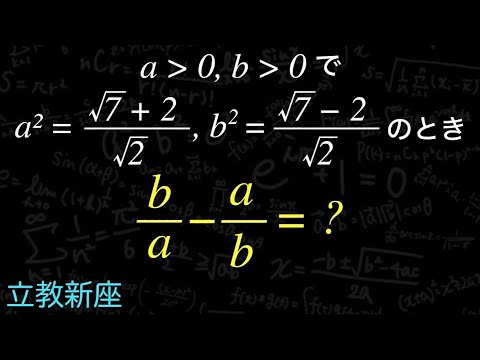
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$a\gt 0,b\gt 0$
$\displaystyle a^2=\frac{\sqrt{7}+2}{\sqrt{2}},b^2=\frac{\sqrt{7}-2}{\sqrt{2}}$のとき次の値を求めよ
$\displaystyle \frac{b}{a}-\frac{a}{b}=?$
この動画を見る
$a\gt 0,b\gt 0$
$\displaystyle a^2=\frac{\sqrt{7}+2}{\sqrt{2}},b^2=\frac{\sqrt{7}-2}{\sqrt{2}}$のとき次の値を求めよ
$\displaystyle \frac{b}{a}-\frac{a}{b}=?$
【年号をヒントだと…!】計算:立教新座高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2024^2-4047\times2025+2031\times2019$を計算せよ。
この動画を見る
$2024^2-4047\times2025+2031\times2019$を計算せよ。
【論理的に合理的に…!】整数:立教新座高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#2次方程式#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{24}{a^2+4a+3}$が$\color{blue}{自然数}$となるような$\color{orange}{整数a}$は$\color{orange}{何個}$ありますか.
※$ a^2+4a+3$は$0$ではない.
立教新座高校過去問
この動画を見る
$ \dfrac{24}{a^2+4a+3}$が$\color{blue}{自然数}$となるような$\color{orange}{整数a}$は$\color{orange}{何個}$ありますか.
※$ a^2+4a+3$は$0$ではない.
立教新座高校過去問
【5分で高校入試から大学受験まで!「型」を見抜け!】整数:立教新座高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
この動画を見る
入試問題 立教新座高等学校
$x$と$y$は自然数とします。
【方程式】
$4x^2-9y^2=31
を満たす x,y の値をそれぞれ求めなさい。
【解き方は1つじゃない!】二次方程式:立教新座高校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立教新座高等学校
二次方程式
$(x-\sqrt{ 2 })^2+6(x-\sqrt{ 2 })+7=0$
を解きなさい。
この動画を見る
入試問題 立教新座高等学校
二次方程式
$(x-\sqrt{ 2 })^2+6(x-\sqrt{ 2 })+7=0$
を解きなさい。
立教新座2016(高校入試)
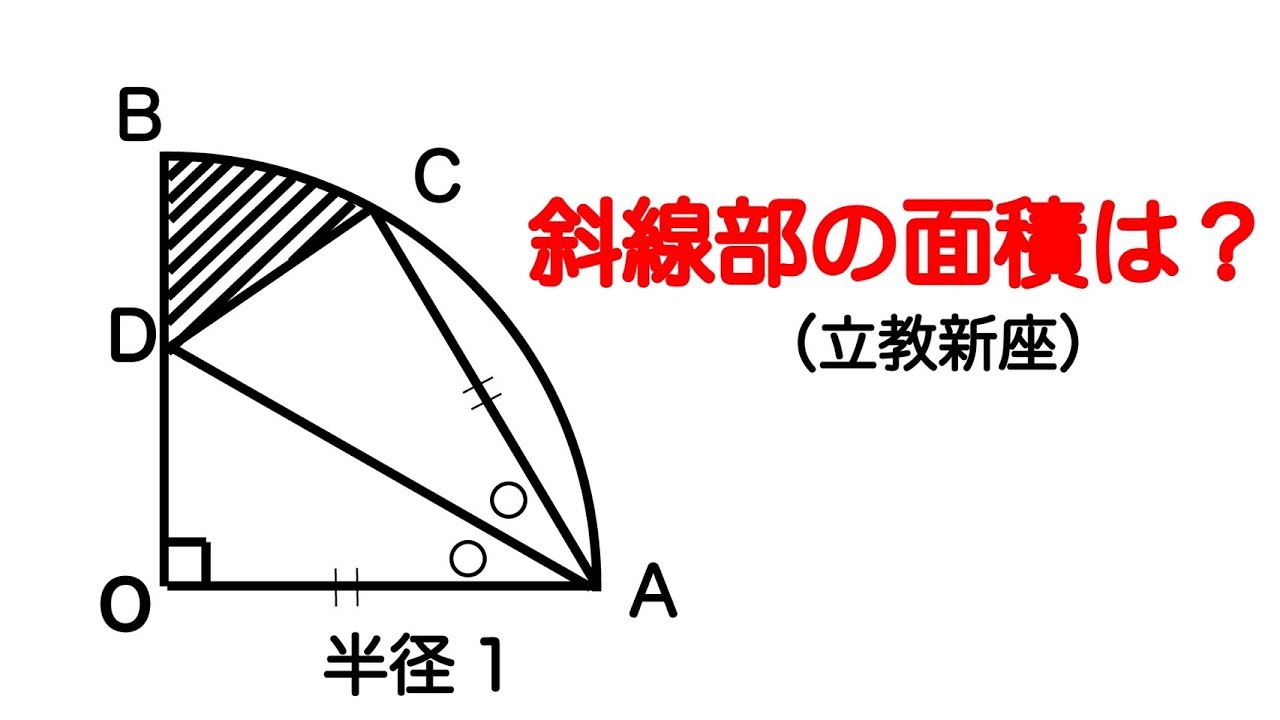
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
この動画を見る
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
