 東京学芸大学附属高等学校
東京学芸大学附属高等学校
 東京学芸大学附属高等学校
東京学芸大学附属高等学校
【ルールに忠実に…!】平方根:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
この動画を見る
$ \dfrac{\sqrt{(-2)^2}(\sqrt2+\sqrt3)^2}{\sqrt2}+\dfrac{(3-\sqrt6)^2}{\sqrt3}$
を計算しなさい.
東京学芸大附属高校過去問
【中学の計算をまとめる3分間】平方根:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京学芸大学附属高等学校
$(\sqrt{ 2^2 }+\sqrt{ 3 }-\sqrt{ 2 }+\sqrt{ 1^2 })\{ \sqrt{ -(2)^2 } +\sqrt{ 3 } + \sqrt{ 2 }+ \sqrt{ -(1)^2 } \}$
を求めよ。
この動画を見る
入試問題 東京学芸大学附属高等学校
$(\sqrt{ 2^2 }+\sqrt{ 3 }-\sqrt{ 2 }+\sqrt{ 1^2 })\{ \sqrt{ -(2)^2 } +\sqrt{ 3 } + \sqrt{ 2 }+ \sqrt{ -(1)^2 } \}$
を求めよ。
確率:東京学芸大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
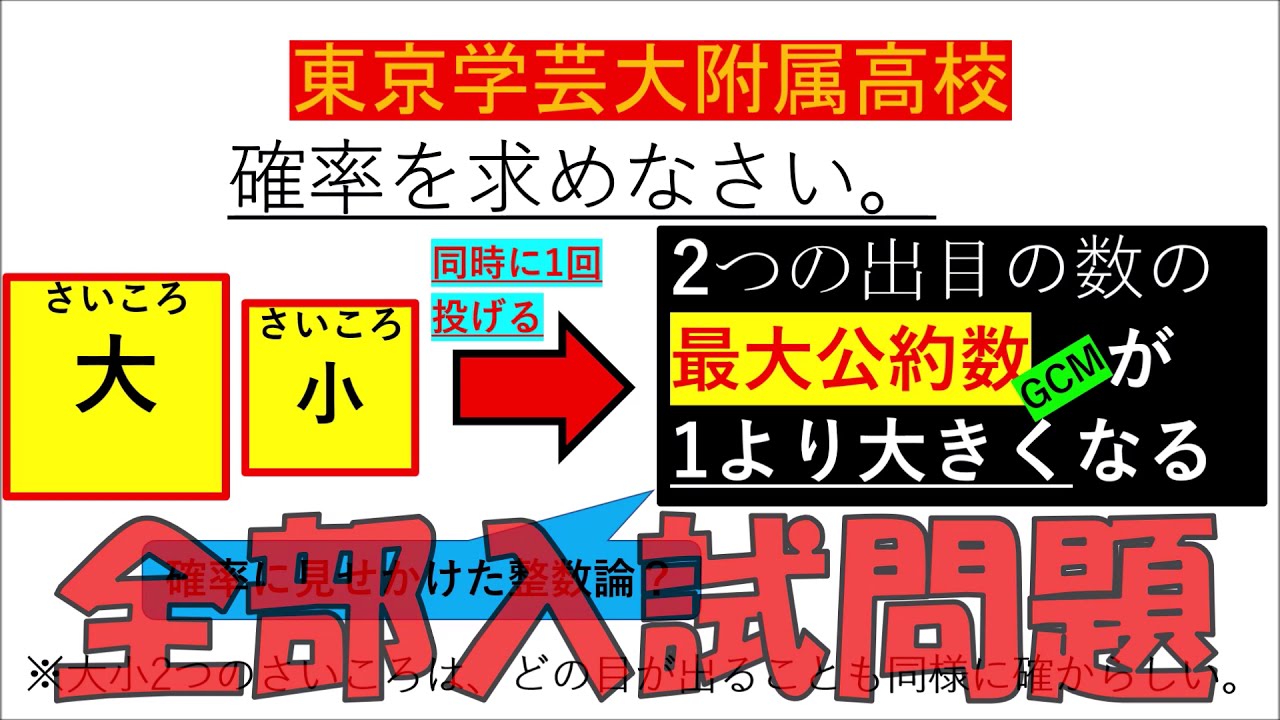
入試問題 東京学芸大学附属高等学校
確率を求めなさい。
同時に1回投げ、2つの出目の数の
最大公約数が
1より大きくなる
※大小2つのさいころは、どの目が出ることも同様に確からしい。
この動画を見る
入試問題 東京学芸大学附属高等学校
確率を求めなさい。
同時に1回投げ、2つの出目の数の
最大公約数が
1より大きくなる
※大小2つのさいころは、どの目が出ることも同様に確からしい。
平面図形:東京学芸大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
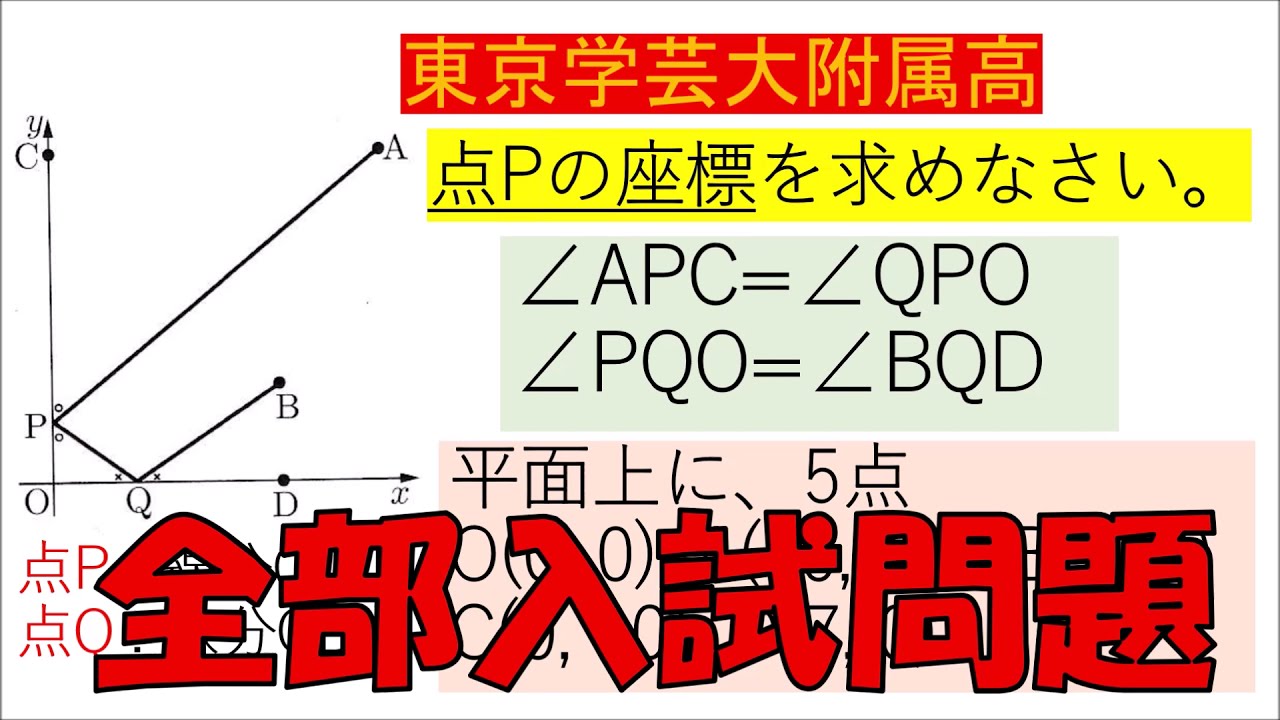
入試問題 東京学芸大学附属高等学校
点$P$の座標を求めなさい。
$\angle APC=\angle QPO$
$\angle PQO=\angle BQD$
平面上に、5点
点$P$:線分$OC$上
点$Q$:線分$OD$上
$O(0, 0), A(10, 10), B(7, 3)$
$C(0, 10), D(7, 0)$
この動画を見る
入試問題 東京学芸大学附属高等学校
点$P$の座標を求めなさい。
$\angle APC=\angle QPO$
$\angle PQO=\angle BQD$
平面上に、5点
点$P$:線分$OC$上
点$Q$:線分$OD$上
$O(0, 0), A(10, 10), B(7, 3)$
$C(0, 10), D(7, 0)$
一次関数:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京学芸大学附属高等学校
$\angle APB=90^{ \circ }$であるときの$t$の値を求めなさい。
点$A(-1,0)$、点$B(3,0)$
関数$y = 8x$のグラフ上に点$P$
点$P$:$x$座標を$t$とする。
($t \gt 0$)
この動画を見る
入試問題 東京学芸大学附属高等学校
$\angle APB=90^{ \circ }$であるときの$t$の値を求めなさい。
点$A(-1,0)$、点$B(3,0)$
関数$y = 8x$のグラフ上に点$P$
点$P$:$x$座標を$t$とする。
($t \gt 0$)
