 中央大学附属高等学校
中央大学附属高等学校
 中央大学附属高等学校
中央大学附属高等学校
気づけば爽快!!平方根の計算 中央大学附属

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
${(\sqrt{5}+\sqrt{3})^2}-{\sqrt{2}(\sqrt{10}+\sqrt{6})(\sqrt{5}-\sqrt{3})}+{(\sqrt{5}-\sqrt{3})^2}$
この動画を見る
${(\sqrt{5}+\sqrt{3})^2}-{\sqrt{2}(\sqrt{10}+\sqrt{6})(\sqrt{5}-\sqrt{3})}+{(\sqrt{5}-\sqrt{3})^2}$
【考えれば考えるほど…!】整数:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$1963^{1963}$を10で割った余りを求めなさい。
この動画を見る
$1963^{1963}$を10で割った余りを求めなさい。
【とても大切な解法…!】二次方程式:中央大学附属高等学校~全国入試解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#2次方程式#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式 $3\left(x+1\right)^2=2\left(x+1\right)\left(x-6\right)-\left(x+1\right)\left(x-1\right)\;$を解きなさい。
この動画を見る
2次方程式 $3\left(x+1\right)^2=2\left(x+1\right)\left(x-6\right)-\left(x+1\right)\left(x-1\right)\;$を解きなさい。
【目がくらむ…!】因数分解:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#式の計算(展開、因数分解)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$7a^2x^3y^3-42a^2x^2y^4+56a^2xy^5$を因数分解しなさい。
この動画を見る
$7a^2x^3y^3-42a^2x^2y^4+56a^2xy^5$を因数分解しなさい。
【得意になる…!】整数:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$S=n^4-5n^3-10n^2+35n+49$において、$S=-26$のとき$n$の値を求めなさい。ただし、$n$は自然数とする。
この動画を見る
$S=n^4-5n^3-10n^2+35n+49$において、$S=-26$のとき$n$の値を求めなさい。ただし、$n$は自然数とする。
【誘導に乗って…!】因数分解:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$S=n^4-5n^3-10n^2+35n+49$を因数分解しなさい。
この動画を見る
$S=n^4-5n^3-10n^2+35n+49$を因数分解しなさい。
【別解を考えるのも楽しい…!】二次方程式:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 中央大学附属高等学校
二次方程式を解きなさい。
$(3x + 2)(2x – 3) +x - 2 = 2(x + 1)^2$
この動画を見る
入試問題 中央大学附属高等学校
二次方程式を解きなさい。
$(3x + 2)(2x – 3) +x - 2 = 2(x + 1)^2$
【ライバルは多い…!】因数分解:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
この動画を見る
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
高等学校入学試験予想問題:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の各問いに答えよ.
$\boxed{1}$(1)
$ \dfrac{(2x^3z^4)^2}{5x^2y^3}\div \left(\dfrac{x^2z^3}{y}\right)\times \left(-\dfrac{10}{xy^2}\right)$
これを計算せよ.
(2)
$ (x+2)(3x+4)=5x^2+6x+7 $
これを解きなさい.
$\boxed{2}$
図のように,放物線$ y=x^2 $上に点$ A(-1,1)$がある.
$ OA=OP$となるように$ y $軸の正の部分に点$ P $をとる.
また,直線$ AP $と放物線$ y=x^2 $の点$ A $でない交点を$ B $とする.
このとき,次の問いに答えなさい.
(1)点$ P $の座標を求めなさい.
(2)点$ B $の座標を求めなさい.
(3)点$ B $を通って,直線$ OA $に平行な直線と$ y $軸との交点を$ C $とする.
$ \triangle OAP $の面積を$ S $とするとき,
$ \triangle ABC $の面積を$ S $を用いて表しなさい.
$ \boxed{3}$
$ k $番目が$ k $である数の列$ {1,2,3,・・・・・・}$の1番目から
$ n $番目までのすべての数の列の和を
$ \displaystyle \sum_{k=1}^{n}k $で表す.
式で表すと,$ \displaystyle \sum_{k=1}^{n}k=1+2+3+・・・+n$となる.
同様に,$ k $番目が$ k^2 $である数の列$ {1^2,2^2,3^2,・・・・・・}$の
1番目から$ n $番目までのすべての数の列の和を式で表すと,
$ \displaystyle \sum_{k=1}^{n}k^2=1^2+2^2+3^2+・・・+n^2 $となる.
$ \displaystyle \sum_{k=1}^{5}k^3 $を式で表しなさい.
中央大学附属高等学校予想問題
この動画を見る
次の各問いに答えよ.
$\boxed{1}$(1)
$ \dfrac{(2x^3z^4)^2}{5x^2y^3}\div \left(\dfrac{x^2z^3}{y}\right)\times \left(-\dfrac{10}{xy^2}\right)$
これを計算せよ.
(2)
$ (x+2)(3x+4)=5x^2+6x+7 $
これを解きなさい.
$\boxed{2}$
図のように,放物線$ y=x^2 $上に点$ A(-1,1)$がある.
$ OA=OP$となるように$ y $軸の正の部分に点$ P $をとる.
また,直線$ AP $と放物線$ y=x^2 $の点$ A $でない交点を$ B $とする.
このとき,次の問いに答えなさい.
(1)点$ P $の座標を求めなさい.
(2)点$ B $の座標を求めなさい.
(3)点$ B $を通って,直線$ OA $に平行な直線と$ y $軸との交点を$ C $とする.
$ \triangle OAP $の面積を$ S $とするとき,
$ \triangle ABC $の面積を$ S $を用いて表しなさい.
$ \boxed{3}$
$ k $番目が$ k $である数の列$ {1,2,3,・・・・・・}$の1番目から
$ n $番目までのすべての数の列の和を
$ \displaystyle \sum_{k=1}^{n}k $で表す.
式で表すと,$ \displaystyle \sum_{k=1}^{n}k=1+2+3+・・・+n$となる.
同様に,$ k $番目が$ k^2 $である数の列$ {1^2,2^2,3^2,・・・・・・}$の
1番目から$ n $番目までのすべての数の列の和を式で表すと,
$ \displaystyle \sum_{k=1}^{n}k^2=1^2+2^2+3^2+・・・+n^2 $となる.
$ \displaystyle \sum_{k=1}^{5}k^3 $を式で表しなさい.
中央大学附属高等学校予想問題
【ヒントを活かせ…!】二次方程式:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
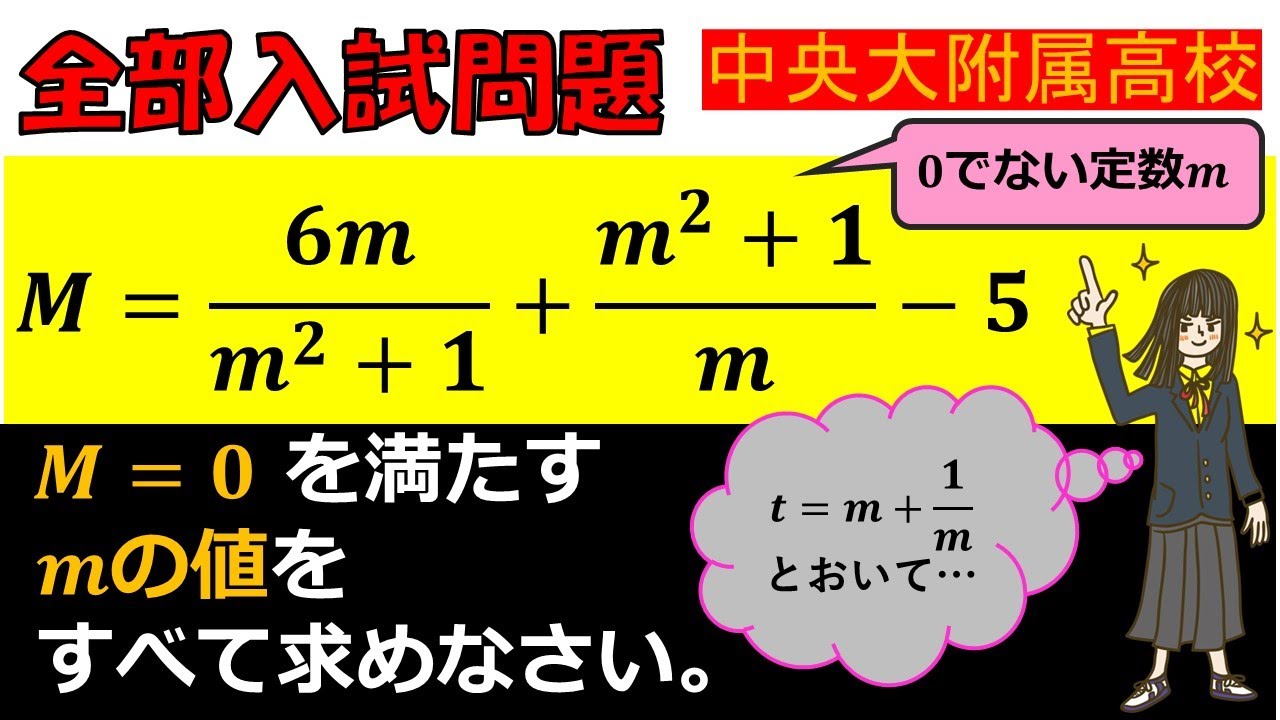
$ M=\dfrac{6m}{m^2+1}+\dfrac{m^2+1}{m}-5 $
$ M=0 $を満たす$ m $の値をすべて求めなさい.
中央大附属高校過去問
この動画を見る
$ M=\dfrac{6m}{m^2+1}+\dfrac{m^2+1}{m}-5 $
$ M=0 $を満たす$ m $の値をすべて求めなさい.
中央大附属高校過去問
【何が見えてくるのか!】平方根:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (\sqrt5+\sqrt3)^2-\sqrt2(\sqrt{10}+\sqrt6)\times (\sqrt5-\sqrt3)+(\sqrt5-\sqrt3)^2 $
を計算しなさい.
中央大附属高校過去問
この動画を見る
$ (\sqrt5+\sqrt3)^2-\sqrt2(\sqrt{10}+\sqrt6)\times (\sqrt5-\sqrt3)+(\sqrt5-\sqrt3)^2 $
を計算しなさい.
中央大附属高校過去問
【3分で数学が好きになる!?】連立方程式:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
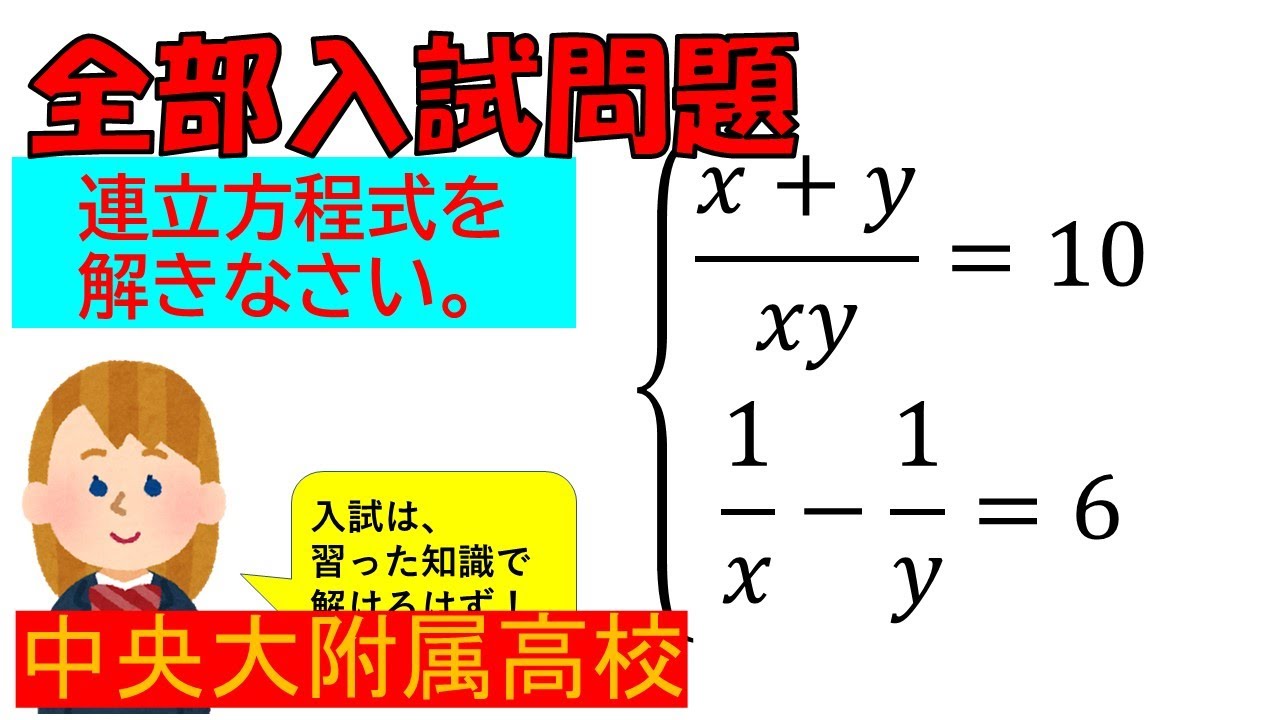
入試問題 中央大学附属高等学校
連立方程式を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x+y}{xy } = 10 \\
\displaystyle \frac{1}{ x }- \displaystyle \frac{1}{ y }=6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 中央大学附属高等学校
連立方程式を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x+y}{xy } = 10 \\
\displaystyle \frac{1}{ x }- \displaystyle \frac{1}{ y }=6
\end{array}
\right.
\end{eqnarray}$
