方程式
方程式
【高校受験対策】数学-死守38
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#連立方程式#２次方程式#1次関数#確率#2次関数#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察４（受験編）
単元：
#中１数学#方程式#数Ⅱ#数と式#式と証明#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#一次不等式（不等式・絶対値のある方程式・不等式）#恒等式・等式・不等式の証明#文字と式
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}\ n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$\ a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}$
この動画を見る
${\Large\boxed{1}}\ n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$\ a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}$
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察３（受験編）
単元：
#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#数と式#式と証明#式の計算（整式・展開・因数分解）#一次不等式（不等式・絶対値のある方程式・不等式）#恒等式・等式・不等式の証明#文字と式
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
この動画を見る
${\Large\boxed{1}}$ $\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[4]{abcd}$ を既知として、$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$ を証明せよ。
ただし、$a,b,c,d$は全て正の数であるとする。
${\Large\boxed{2}}\ \boxed{1}$を利用して、$n$個の変数の相加・相乗平均の関係を証明せよ。
つまり、$n$個の正の数$a_1,a_2,\cdot,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n} $$\geqq \sqrt[n]{a_1a_2\cdots a_n}$
【高校受験対策】数学-死守31
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#平方根#２次方程式#確率#2次関数#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
この動画を見る
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
【高校受験対策】数学-死守30
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#２次方程式#空間図形#立体図形#立体図形その他
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-7+11$を計算しなさい。
②$9\times \left(-\dfrac{4}{15}\right)$を計算しなさい。
③$- 4(3 - 2x) + (- 6x + 9)$を計算しなさい。
④$\sqrt{45}-\sqrt5$を計算しなさい。
⑤一次方程式$2x - 15 = - x$を解きなさい。
⑥$x ^ 2 + 3x - 28 $を因数分解しなさい。
⑦二次方程式$2x ^ 2 + 3x - 4 = 0$を解きなさい。
⑧「1個$ag$のおもり3個の重さは$100g$以下である。」という数量の関係を
不等式で表しなさい。
⑨関数$y=2x-3$のグラフに平行な直線の式を、
次のア~カからすべて選び番号を書きなさい。
ア→$y = - 2x - 3$
イ→$y = 2x ^ 2$
ウ→$y = 5x - 3$
エ→$y = 2x + 3$
オ→$y = \dfrac{1}{2}x$
カ→$y = 2x$
⑩$x = 2,y=1$が解になっている連立方程式を、次のア~ウから1つ選びなさい。
$ア→\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
x+4y=9
\end{array}
\right.
\end{eqnarray}$
$イ→\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=7 \\
5x-3y=0
\end{array}
\right.
\end{eqnarray}$
$ウ→\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y=5 \\
-x+4y=2
\end{array}
\right.
\end{eqnarray}$
⑪方程式$3x - 4y = 5x - y = 17$を解きなさい。
⑫底面の半径が3cm、高さが5cmの円柱がある。
この円柱の側面積を求めなさい。
この動画を見る
①$-7+11$を計算しなさい。
②$9\times \left(-\dfrac{4}{15}\right)$を計算しなさい。
③$- 4(3 - 2x) + (- 6x + 9)$を計算しなさい。
④$\sqrt{45}-\sqrt5$を計算しなさい。
⑤一次方程式$2x - 15 = - x$を解きなさい。
⑥$x ^ 2 + 3x - 28 $を因数分解しなさい。
⑦二次方程式$2x ^ 2 + 3x - 4 = 0$を解きなさい。
⑧「1個$ag$のおもり3個の重さは$100g$以下である。」という数量の関係を
不等式で表しなさい。
⑨関数$y=2x-3$のグラフに平行な直線の式を、
次のア~カからすべて選び番号を書きなさい。
ア→$y = - 2x - 3$
イ→$y = 2x ^ 2$
ウ→$y = 5x - 3$
エ→$y = 2x + 3$
オ→$y = \dfrac{1}{2}x$
カ→$y = 2x$
⑩$x = 2,y=1$が解になっている連立方程式を、次のア~ウから1つ選びなさい。
$ア→\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
x+4y=9
\end{array}
\right.
\end{eqnarray}$
$イ→\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=7 \\
5x-3y=0
\end{array}
\right.
\end{eqnarray}$
$ウ→\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y=5 \\
-x+4y=2
\end{array}
\right.
\end{eqnarray}$
⑪方程式$3x - 4y = 5x - y = 17$を解きなさい。
⑫底面の半径が3cm、高さが5cmの円柱がある。
この円柱の側面積を求めなさい。
【テスト対策・中１】３章－２
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の方程式の解き方はまちがっている。
ア～エで、最初にまちがえた式を選び、記号で答えなさい。
また、正しい解を求めなさい。
①$x-1=3(3+x)$
$x-1=9+3x$・・・ア
$x-3x=0-1$・・・イ
$-2x=8$・・・ウ
$x=-4$・・・エ
②$\dfrac{x}{4}-1=\dfrac{x-2}{3}$
$3x-12=4x-2$・・・ア
$3x-4x=-2+12$・・・イ
$-x=10$・・・ウ
$x=-10$・・・エ
この動画を見る
次の方程式の解き方はまちがっている。
ア～エで、最初にまちがえた式を選び、記号で答えなさい。
また、正しい解を求めなさい。
①$x-1=3(3+x)$
$x-1=9+3x$・・・ア
$x-3x=0-1$・・・イ
$-2x=8$・・・ウ
$x=-4$・・・エ
②$\dfrac{x}{4}-1=\dfrac{x-2}{3}$
$3x-12=4x-2$・・・ア
$3x-4x=-2+12$・・・イ
$-x=10$・・・ウ
$x=-10$・・・エ
【テスト対策・中１】３章－１
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の方程式を解きなさい。
①$5x-2=3x+4$
②$13=6-(2x-5)$
③$3(3x-2)=-3(5-x)$
④$\dfrac{1}{3}x+4=2+x$
⑤$\dfrac{x-1}{2}-2=\dfrac{2x-1}{3}$
⑥$0.1(x+1)=0.06(x+15)$
この動画を見る
次の方程式を解きなさい。
①$5x-2=3x+4$
②$13=6-(2x-5)$
③$3(3x-2)=-3(5-x)$
④$\dfrac{1}{3}x+4=2+x$
⑤$\dfrac{x-1}{2}-2=\dfrac{2x-1}{3}$
⑥$0.1(x+1)=0.06(x+15)$
【高校受験対策】数学－死守２３
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#２次方程式#確率#立体図形#立体切断#立体図形その他#三角形と四角形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
この動画を見る
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
【高校受験対策】数学－死守２０
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#数と式#比例・反比例#確率#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#単位・比と割合・比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
この動画を見る
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
【高校受験対策】数学－死守１９
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#２次方程式#比例・反比例#確率#文章題#文章題その他#標本調査
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$8-(-13)$を計算しなさい.
②$(- 3) ^ 2 + \left(-\dfrac{1}{3}\right)\times 6$ を計算しなさい.
③$(7a - 4b) + \dfrac{1}{2}(2b - 6a)$ を計算しなさい.
④方程式$ 0.2(x - 2) = x + 1.2$ を解きなさい.
⑤$\sqrt{48}-\sqrt{27}+5\sqrt3$を計算しなさい.
⑥二次方程式$x ^ 2 + 7x + 5 = 0 $を解きなさい.
⑦$y$は$x$の2乗に比例し,
$ x = 2 $のとき,$y=1$である.
$y$を$x$の式で表しなさい.
⑧右の資料は,ある生徒が受けた第1回から第6回までの数学のテストの得点の記録のうち,
第1回から第5回までの得点の記録である.
第1回から第6回までの得点の中央値が80点となるとき,
第6回のテストの得点を求めなさい.
$\boxed{83 \quad 78\quad 74\quad 77 \quad 96}$ (単位:点)
⑨$m$と$n$は連続する正の整数である.
次のア~エのうちから,次の値が偶数となるものを一つ選び,
符号で答えなさい.ただし,$m \lt n$とする.
ア.$m+n$
イ.$n-m$
ウ.m + n + 2$
エ.$mn$
⑩箱の中に同じ大きさの白い球だけがたくさん入っている.
この白い球が何個あるか,標本調査を行って推測しょうと考えた.
そこでオレンジ色の球200個を箱に入れてよくかき混ぜ,
そこから50個を無作為に抽出したところ,
オレンジ色の球が4個含まれていた.
はじめに箱の中に入っていた白い球の個数を推測しなさい
①箱の中に$②,③,④,⑥,⑧,⑨$のカードがそれぞれ1枚ずつ入っている.
この箱から同時に2枚取り出すとき,
取り出した2枚のカードに書かれた数の最小公倍数が,
1桁の数になる確率を求めなさい.
ただし,どのカードの取り出し方も同様に確からしいものとする.
この動画を見る
①$8-(-13)$を計算しなさい.
②$(- 3) ^ 2 + \left(-\dfrac{1}{3}\right)\times 6$ を計算しなさい.
③$(7a - 4b) + \dfrac{1}{2}(2b - 6a)$ を計算しなさい.
④方程式$ 0.2(x - 2) = x + 1.2$ を解きなさい.
⑤$\sqrt{48}-\sqrt{27}+5\sqrt3$を計算しなさい.
⑥二次方程式$x ^ 2 + 7x + 5 = 0 $を解きなさい.
⑦$y$は$x$の2乗に比例し,
$ x = 2 $のとき,$y=1$である.
$y$を$x$の式で表しなさい.
⑧右の資料は,ある生徒が受けた第1回から第6回までの数学のテストの得点の記録のうち,
第1回から第5回までの得点の記録である.
第1回から第6回までの得点の中央値が80点となるとき,
第6回のテストの得点を求めなさい.
$\boxed{83 \quad 78\quad 74\quad 77 \quad 96}$ (単位:点)
⑨$m$と$n$は連続する正の整数である.
次のア~エのうちから,次の値が偶数となるものを一つ選び,
符号で答えなさい.ただし,$m \lt n$とする.
ア.$m+n$
イ.$n-m$
ウ.m + n + 2$
エ.$mn$
⑩箱の中に同じ大きさの白い球だけがたくさん入っている.
この白い球が何個あるか,標本調査を行って推測しょうと考えた.
そこでオレンジ色の球200個を箱に入れてよくかき混ぜ,
そこから50個を無作為に抽出したところ,
オレンジ色の球が4個含まれていた.
はじめに箱の中に入っていた白い球の個数を推測しなさい
①箱の中に$②,③,④,⑥,⑧,⑨$のカードがそれぞれ1枚ずつ入っている.
この箱から同時に2枚取り出すとき,
取り出した2枚のカードに書かれた数の最小公倍数が,
1桁の数になる確率を求めなさい.
ただし,どのカードの取り出し方も同様に確からしいものとする.
【高校受験対策】数学－死守９
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#円#表とグラフ#表とグラフ・集合
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問に答えよ.
①$- 7 + 8 \times \left(-\dfrac{1}{4}\right)$を計算せよ.
②$9(a + b) - (a + 3b) $を計算せよ.
③$(\sqrt7 + 6)(\sqrt7 - 2)$ を計算せよ.
④一次方程式$ x - 5 = 3x + 1 $を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=9 \\
x-6y=8
\end{array}
\right.
\end{eqnarray}$
⑥一次方程式 $x ^ 2 - 12x + 35 = 0 $を解け.
⑦右の表は,
ある中学校の3年生男子全体のハンドボール投げの記録を,
度数分布表に整理したものである.
26m以上投げた生徒の人数は,
3年生男子全体の何%か.
⑧右の図で,2点$C,D$は,線分$AB$を直径とする半円$O$の
$\stackrel{\huge\frown}{AB}$上にある点で,
$\stackrel{\huge\frown}{AC}=\dfrac{4}{9}\stackrel{\huge\frown}{AB},\stackrel{\huge\frown}{BD}=\dfrac{1}{3}\stackrel{\huge\frown}{AB}$である.
線分$AD$と線分$BC$の交点を$E$とするとき,
$\angle AEC$の大きさは何度か.
図は動画内を参照
この動画を見る
次の各問に答えよ.
①$- 7 + 8 \times \left(-\dfrac{1}{4}\right)$を計算せよ.
②$9(a + b) - (a + 3b) $を計算せよ.
③$(\sqrt7 + 6)(\sqrt7 - 2)$ を計算せよ.
④一次方程式$ x - 5 = 3x + 1 $を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-y=9 \\
x-6y=8
\end{array}
\right.
\end{eqnarray}$
⑥一次方程式 $x ^ 2 - 12x + 35 = 0 $を解け.
⑦右の表は,
ある中学校の3年生男子全体のハンドボール投げの記録を,
度数分布表に整理したものである.
26m以上投げた生徒の人数は,
3年生男子全体の何%か.
⑧右の図で,2点$C,D$は,線分$AB$を直径とする半円$O$の
$\stackrel{\huge\frown}{AB}$上にある点で,
$\stackrel{\huge\frown}{AC}=\dfrac{4}{9}\stackrel{\huge\frown}{AB},\stackrel{\huge\frown}{BD}=\dfrac{1}{3}\stackrel{\huge\frown}{AB}$である.
線分$AD$と線分$BC$の交点を$E$とするとき,
$\angle AEC$の大きさは何度か.
図は動画内を参照
【高校受験対策】数学－死守４
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#２次方程式#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
この動画を見る
次の各問に答えよ.
①$7+3\times (-5)$を計算せよ.
②$3(2a+1)-4(a+2)$を計算せよ.
③$a=-3,b=6$のとき,
$-a^2+2b$の値を求めよ.
④$\dfrac{27}{\sqrt3}-\sqrt{48}$を計算せよ.
⑤1次方程式$x-9=3(x-1)$を解け.
⑥2次方程式$x(x-6)=-4(x-2)$を解け.
⑦$y$は$x$に反比例し,$x=-3$のとき,$y=-8$である.
$x=-4$のときの$y$の値を求めよ.
【高校受験対策】死守－３
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#２次方程式#1次関数#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
この動画を見る
次の各問に答えよ.
①$6+4 \times \left(-\dfrac{1}{2}\right)$を計算せよ.
②$8a+b-(a-7b)$を計算せよ.
③$(\sqrt5 +\sqrt 3)(\sqrt 5-\sqrt3)$を計算せよ.
④1次方程式$9x+2=8(x+1)$を解け.
⑤連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=4 \\
6x+5y=-7
\end{array}
\right.
\end{eqnarray}$を解け.
⑥2次方程式$x^2-8x-9=0$を解け.
⑦関数$y=\dfrac{1}{3}x^2$について,
$x$の値を3から9まで増加するときの割合を求めよ.
【高校受験対策】死守－１
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#連立方程式#式の計算（展開、因数分解）#２次方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
この動画を見る
①$24 \div (7-4)$を計算しなさい.
②$\dfrac{1}{2}+\dfrac{2}{5}$を計算しなさい.
③$7+(-3)\times 4$を計算しなさい.
④$(5x-y)-3(x-5y)$を計算しなさい.
⑤下の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x = 3y-2 \\
4x-7y=2
\end{array}
\right.
\end{eqnarray}$
⑥$\sqrt{32}-\sqrt 8+\sqrt2 $を計算しなさい.
⑦$x^2-36y^2$を因数分解しなさい.
⑧方程式$x^2+7x+2=0$を解きなさい.
【中１ P.95】方程式の計算特訓②
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$
この動画を見る
2.次の計算をしよう.
$\boxed{1} \quad x:5=8:2$
$\boxed{2} \quad 3:x=7:3$
$\boxed{3} \quad (x-5):3=16:12$
$\boxed{4} \quad 2:x=3:(x+5)$
$\boxed{5} \quad (x+7):6=x:\dfrac{5}{2}$
$\boxed{6} \quad (x-2):3=(x+1):5$
【中１ P.94】方程式の計算特訓①
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
この動画を見る
1.次の計算をしよう.
$\boxed{1} \quad 5x+4=3x+12$
$\boxed{2} \quad 9-x=5$
$\boxed{3} \quad 3(x-4)=5x+2$
$\boxed{4} \quad \dfrac{3}{2}x-1=4-x$
$\boxed{5} \quad \dfrac{x+4}{3}+1=\dfrac{3x-7}{2}$
$\boxed{6} \quad 0.4x+0.5=2.6-0.3x$
$\boxed{7} \quad 1.5x-3=\dfrac{6}{5}x-0.3$
$\boxed{8} \quad \dfrac{1}{2}x+\dfrac{3}{4}=\dfrac{3}{8}x-\dfrac{1}{2}$
【受験対策】 数学－小問①
単元：
#数学(中学生)#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
この動画を見る
◎次の計算をしよう。
①$-5-8 \times \displaystyle \frac{1}{4}$
②$-3+5 \times (-1)^3$
③$4(2x-y)-3(x+y)$
④$\displaystyle \frac{1}{2}(3a-2b)-(2a-b)$
⑤一次方程式$x-7=9(x+1)$を解こう。
⑥等式$2a-3b=1$を$b$について解こう。
⑦等式$a=\displaystyle \frac{b+c}{2}$をcについて解こう。
中学数学（方程式・高校入試対策）【篠原好】
【中1 数学】中1-45 変域
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
x,yのような①＿＿＿＿の取る値の範囲を②＿＿＿＿っていうよ！
◎xの変域を不等号を使って表そう！
③-2以上6以下
④-9より大きくｰ2未満
⑤6以上8未満
⑥3以上7より小さい
⑦-5より大きく0以下
※図は動画内参照
この動画を見る
x,yのような①＿＿＿＿の取る値の範囲を②＿＿＿＿っていうよ！
◎xの変域を不等号を使って表そう！
③-2以上6以下
④-9より大きくｰ2未満
⑤6以上8未満
⑥3以上7より小さい
⑦-5より大きく0以下
※図は動画内参照
【中1 数学】中1-42 方程式の利用⑩ 比例式+おまけ編
単元：
#数学(中学生)#中１数学#方程式#比例・反比例
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①4本で380円のジュースを14本買うといくら？
②コーヒー80mLと牛乳200mLを混ぜてコーヒー牛乳を作る。
同じ割合でつくるとき、コーヒー100mLに何mLの牛乳を混ぜればいい？
③30kmの距離を12cmの長さで表している地図がある。
9cm離れた2つの点の実際の距離は何km？
④現在さとし君は9歳で、お父さんは41歳です。
お父さんの年齢がさとし君の年齢の3倍になるのは何年後？
この動画を見る
①4本で380円のジュースを14本買うといくら？
②コーヒー80mLと牛乳200mLを混ぜてコーヒー牛乳を作る。
同じ割合でつくるとき、コーヒー100mLに何mLの牛乳を混ぜればいい？
③30kmの距離を12cmの長さで表している地図がある。
9cm離れた2つの点の実際の距離は何km？
④現在さとし君は9歳で、お父さんは41歳です。
お父さんの年齢がさとし君の年齢の3倍になるのは何年後？
【中1 数学】中1-43 解が□であるとき
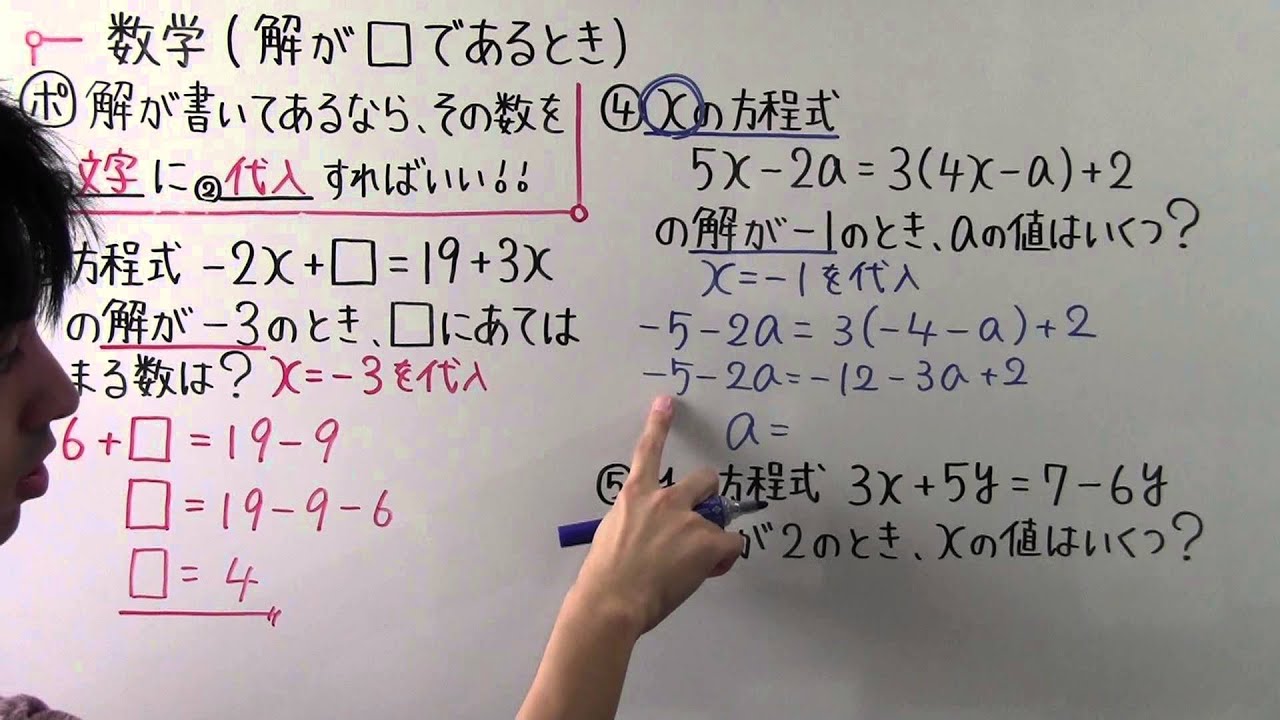
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
解が書いてあるなら、その数を①＿＿に②＿＿すればいい！！
③方程式$-2x+□=19+3x$
の解が$-3$のとき、$□$にあてはまる数は？
④xの方程式
$5x-2a=3(4x-a)+2$
の解が-1のとき、aの値はいくつ？
⑤yの方程式
$3x+5y=7-6y$
の解が2のとき、xの値はいくつ？
この動画を見る
解が書いてあるなら、その数を①＿＿に②＿＿すればいい！！
③方程式$-2x+□=19+3x$
の解が$-3$のとき、$□$にあてはまる数は？
④xの方程式
$5x-2a=3(4x-a)+2$
の解が-1のとき、aの値はいくつ？
⑤yの方程式
$3x+5y=7-6y$
の解が2のとき、xの値はいくつ？
【中1 数学】中1-41 方程式の利用⑨ 昨年と今年編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
昨年と今年の問題は①＿＿を書こう！
◎ある学校の昨年度の生徒数は300人でした。
男子が5％減って、女性が15％増えたので、全体で13人増えた。
昨年度の男子の人数をx人として②～④を解こう！
②昨年度の男子と女子の人数は？
③今年の男子の人数は？
④今年の女子の人数は？
この動画を見る
昨年と今年の問題は①＿＿を書こう！
◎ある学校の昨年度の生徒数は300人でした。
男子が5％減って、女性が15％増えたので、全体で13人増えた。
昨年度の男子の人数をx人として②～④を解こう！
②昨年度の男子と女子の人数は？
③今年の男子の人数は？
④今年の女子の人数は？
【中1 数学】中1-39 方程式の利用⑦ 時間差編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①＿＿＿＿＿＿＿＿＿＿＿＿=時間差
②A地点からB地点まで、行きは分速150mで走り、帰りは分速90mで歩いて帰ったら、かかった時間が8分ちがった。
A地点からB地点までの道のりは？
◎りかさんは、いつも同じ時間に家を出発して分速60mで歩いていくと8時18分に学校につき、分速200mの速さの自転車で行くと7時50分に学校に着く。
③家から学校までの道のりは何m？
④りかさんが家を出発する時刻は？
この動画を見る
①＿＿＿＿＿＿＿＿＿＿＿＿=時間差
②A地点からB地点まで、行きは分速150mで走り、帰りは分速90mで歩いて帰ったら、かかった時間が8分ちがった。
A地点からB地点までの道のりは？
◎りかさんは、いつも同じ時間に家を出発して分速60mで歩いていくと8時18分に学校につき、分速200mの速さの自転車で行くと7時50分に学校に着く。
③家から学校までの道のりは何m？
④りかさんが家を出発する時刻は？
【中1 数学】中1-40 方程式の利用⑧ ある数編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①ある数nの5倍から8をひいた数が、
nの3倍に6をたした数に等しくなる。
ある数nの値はいくつ？
②ある数xの5倍から1ひいた数が、
xに3をたして4倍した数に等しくなる。
ある数xの値はいくつ？
③かいと君が、「俺の背番号は、10たしてから4でわっても、1たしてから3でわっても同じ数なんだ！」と言いました。
かいと君の背番号は何番？
この動画を見る
①ある数nの5倍から8をひいた数が、
nの3倍に6をたした数に等しくなる。
ある数nの値はいくつ？
②ある数xの5倍から1ひいた数が、
xに3をたして4倍した数に等しくなる。
ある数xの値はいくつ？
③かいと君が、「俺の背番号は、10たしてから4でわっても、1たしてから3でわっても同じ数なんだ！」と言いました。
かいと君の背番号は何番？
【中1 数学】中1-38 方程式の利用⑥ ２つの速さ編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①たくみ君は家から1920m離れた友達の家まで行くのに、はじめは
分速120mで走り、途中から分速80mで歩いたので21分かかった。
走った道のりと歩いた道のりは何m？
②おさむ君は家から10km離れた友達の家まで行くのに、バス停まで時速4kmで歩いていき、そこから時速32kmのバスに乗っていったので45分かかった。
歩いた道のりとバスに乗っていった道のりは何km？
この動画を見る
①たくみ君は家から1920m離れた友達の家まで行くのに、はじめは
分速120mで走り、途中から分速80mで歩いたので21分かかった。
走った道のりと歩いた道のりは何m？
②おさむ君は家から10km離れた友達の家まで行くのに、バス停まで時速4kmで歩いていき、そこから時速32kmのバスに乗っていったので45分かかった。
歩いた道のりとバスに乗っていった道のりは何km？
【中1 数学】中1-37 方程式の利用⑤ 追いつく編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
みはじの問題は①＿＿を書こう！
◎兄が1800m離れたコンビニに向かって家を出発した。
それから10分後に、妹が兄が忘れた財布を持って、自転車で同じ道を追いかけた。
兄は分速90m、妹は分速270mで進むとする。
②妹が出発してから何分後に追いつく？
③家から何m離れたところで追いつく？
④もし妹が16分後に家を出たとしたら、兄がコンビニに着くまでに追いつける？
(理由も答えてね！)
この動画を見る
みはじの問題は①＿＿を書こう！
◎兄が1800m離れたコンビニに向かって家を出発した。
それから10分後に、妹が兄が忘れた財布を持って、自転車で同じ道を追いかけた。
兄は分速90m、妹は分速270mで進むとする。
②妹が出発してから何分後に追いつく？
③家から何m離れたところで追いつく？
④もし妹が16分後に家を出たとしたら、兄がコンビニに着くまでに追いつける？
(理由も答えてね！)
【中1 数学】中1-36 方程式の利用④ 長いす編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①長いすを何脚か並べました。
生徒が①客に4人ずつ座ると7人が座れず、5人ずつ座ると3人だけ座った長いす1脚できた。
長いすの数と生徒数は？
②修学旅行でホテルの部屋を何室か予約した。
生徒が1室6人ずつ入ると17人が入れず、8人ずつ入ると5人の部屋が1室できる。
予約した部屋数と生徒数は？
この動画を見る
①長いすを何脚か並べました。
生徒が①客に4人ずつ座ると7人が座れず、5人ずつ座ると3人だけ座った長いす1脚できた。
長いすの数と生徒数は？
②修学旅行でホテルの部屋を何室か予約した。
生徒が1室6人ずつ入ると17人が入れず、8人ずつ入ると5人の部屋が1室できる。
予約した部屋数と生徒数は？
【中1 数学】中1-35 方程式の利用③ 余りとたりない編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①何人かの子どもにあめを分けるのに、
6個ずつ分けると3個余り、
7個ずつ上げると9個足りない。
子どもの人数とあめの個数は？
②先生へのプレゼントを買うのに、1人500円ずつ集めると1500円余り、一人で400円ずつ集めると1200円不足する。
クラスの人数とプレゼントの値段は？
この動画を見る
①何人かの子どもにあめを分けるのに、
6個ずつ分けると3個余り、
7個ずつ上げると9個足りない。
子どもの人数とあめの個数は？
②先生へのプレゼントを買うのに、1人500円ずつ集めると1500円余り、一人で400円ずつ集めると1200円不足する。
クラスの人数とプレゼントの値段は？
【中1 数学】中1-33 方程式の利用① お金編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
もとめたいものを①＿＿＿＿とおく。
②ケーキを4個買って120円の箱に入れてもらったら1400円でした。
ケーキ1個の値段はいくら？
③2000円で、760円のメロンを1個と130円の梨を何個か買うと、おつりが200円でした。
梨を何個買った？
④りえさんは1790円、妹は1100円持っていて2人とも同じメニューを注文しました。
そうするとりえさんの残金が妹の残金の4倍になりました。
メニューの値段はいくら？
⑤ノート5冊と200円のシャープペン2本の代金は、ノート2冊と80円の消しゴム1個の代金の3倍になった。
ノート1冊の値段はいくら？
この動画を見る
もとめたいものを①＿＿＿＿とおく。
②ケーキを4個買って120円の箱に入れてもらったら1400円でした。
ケーキ1個の値段はいくら？
③2000円で、760円のメロンを1個と130円の梨を何個か買うと、おつりが200円でした。
梨を何個買った？
④りえさんは1790円、妹は1100円持っていて2人とも同じメニューを注文しました。
そうするとりえさんの残金が妹の残金の4倍になりました。
メニューの値段はいくら？
⑤ノート5冊と200円のシャープペン2本の代金は、ノート2冊と80円の消しゴム1個の代金の3倍になった。
ノート1冊の値段はいくら？
【中1 数学】中1-34 方程式の利用 あわせて編
単元：
#数学(中学生)#中１数学#方程式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①150円の梨と120円の桃を合わせて15個買うと、2070円でした。
梨と桃をそれぞれ何個買ったかな？
②370円のケーキと180円のプリンを合わせて8個買い、150円に箱に入れてもらうと、全部で2160円でした。
ケーキとプリンをそれぞれ何個買ったかな？
③とある中学生の人数は、男女合わせて450人で、男子は女子より16人少ない。
男子と女子の人数は何人？
この動画を見る
①150円の梨と120円の桃を合わせて15個買うと、2070円でした。
梨と桃をそれぞれ何個買ったかな？
②370円のケーキと180円のプリンを合わせて8個買い、150円に箱に入れてもらうと、全部で2160円でした。
ケーキとプリンをそれぞれ何個買ったかな？
③とある中学生の人数は、男女合わせて450人で、男子は女子より16人少ない。
男子と女子の人数は何人？