平面図形
平面図形
よくある円のパターン 〇〇をみつけろ！ 灘高校
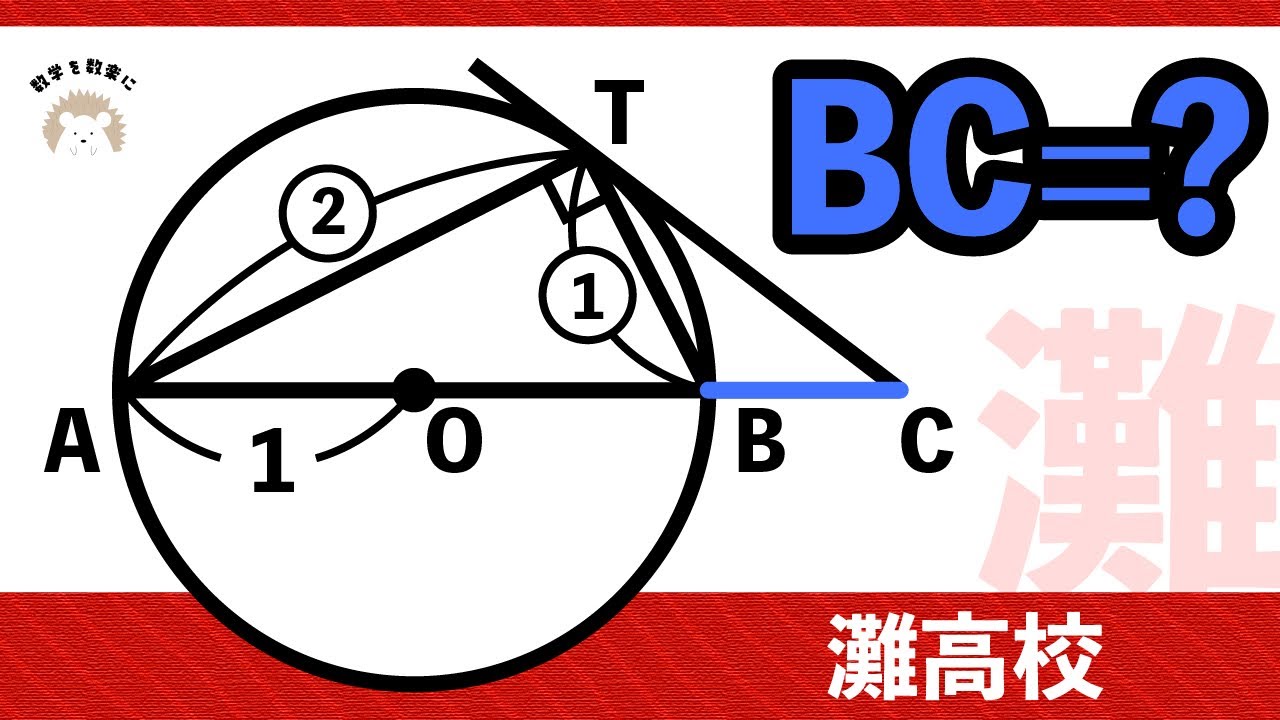
4つの正方形
【中学数学】平面が1つに決まる条件・2直線，直線と平面，平面と平面の位置関係【中１数学】
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
【中学数学】平面が1つに決まる条件・2直線，直線と平面，平面と平面の位置関係についての解説動画です
この動画を見る
【中学数学】平面が1つに決まる条件・2直線，直線と平面，平面と平面の位置関係についての解説動画です
円と角の和
単元：
#算数(中学受験)#数学(中学生)#中１数学#平面図形#角度と面積#平面図形
指導講師：
数学を数楽に
問題文全文(内容文)：
$\angle x+ \angle y= ?$
＊図は動画内参照
この動画を見る
$\angle x+ \angle y= ?$
＊図は動画内参照
それぞれの角は出ていないけど和は求まります！
単元：
#数学(中学生)#中１数学#中２数学#平面図形#三角形と四角形
指導講師：
数学を数楽に
問題文全文(内容文)：
$\angle x+\angle y+\angle z=$
＊図は動画内参照
この動画を見る
$\angle x+\angle y+\angle z=$
＊図は動画内参照
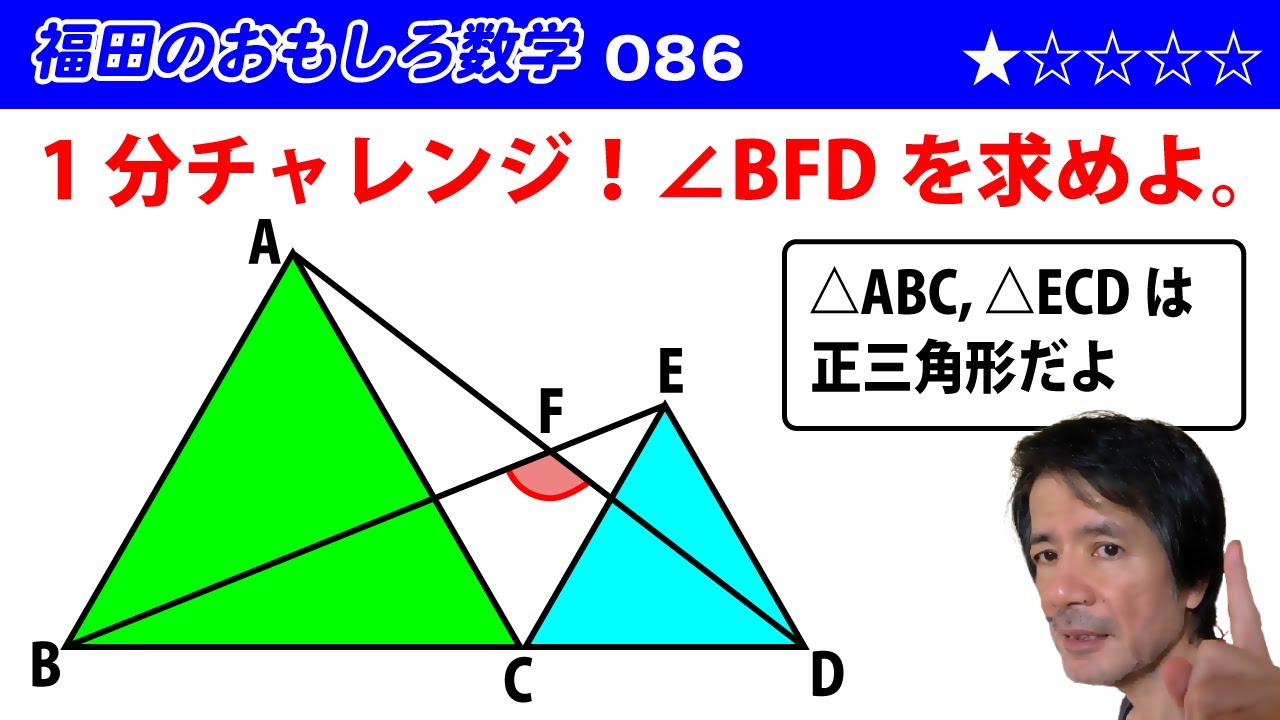
福田のおもしろ数学086〜1分チャレンジ〜正三角形2個で作る核を求めよう
福田のおもしろ数学075〜1分チャレンジ〜扇形から作る円錐の体積
千葉県の難問！？平面図形2024
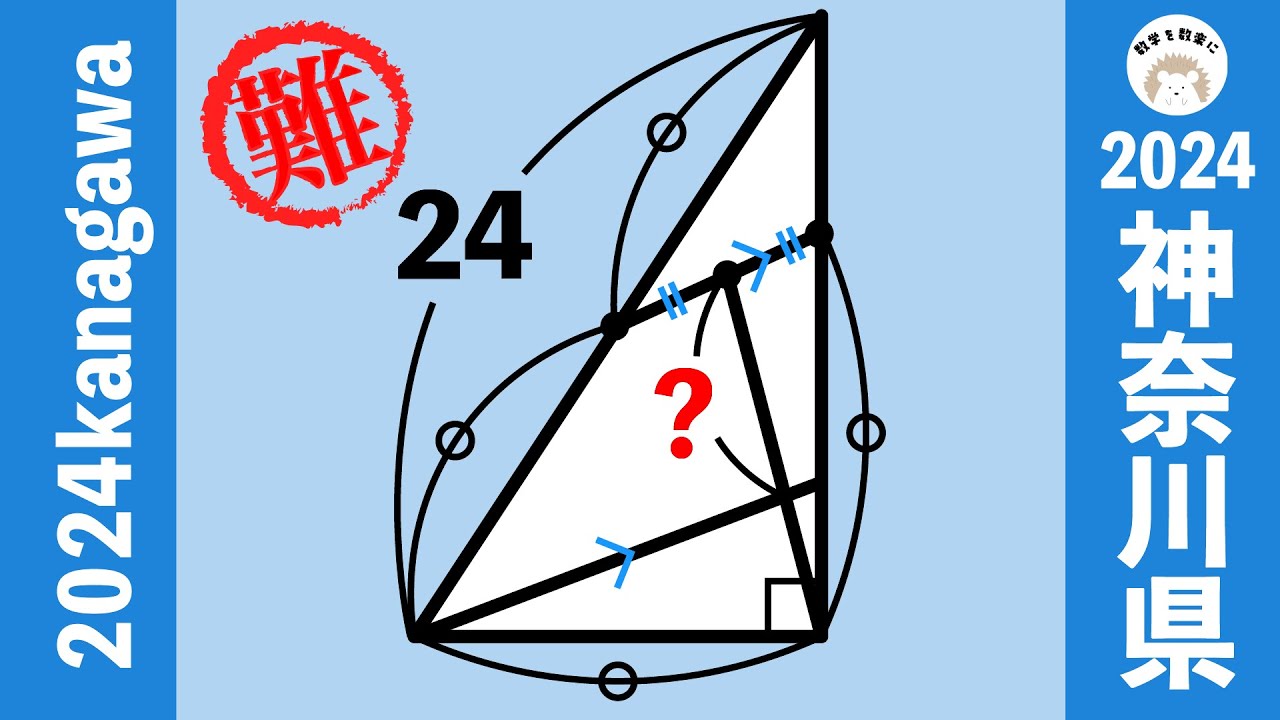
2024神奈川県の平面図形の難問
平面図形 2024京都府（改）
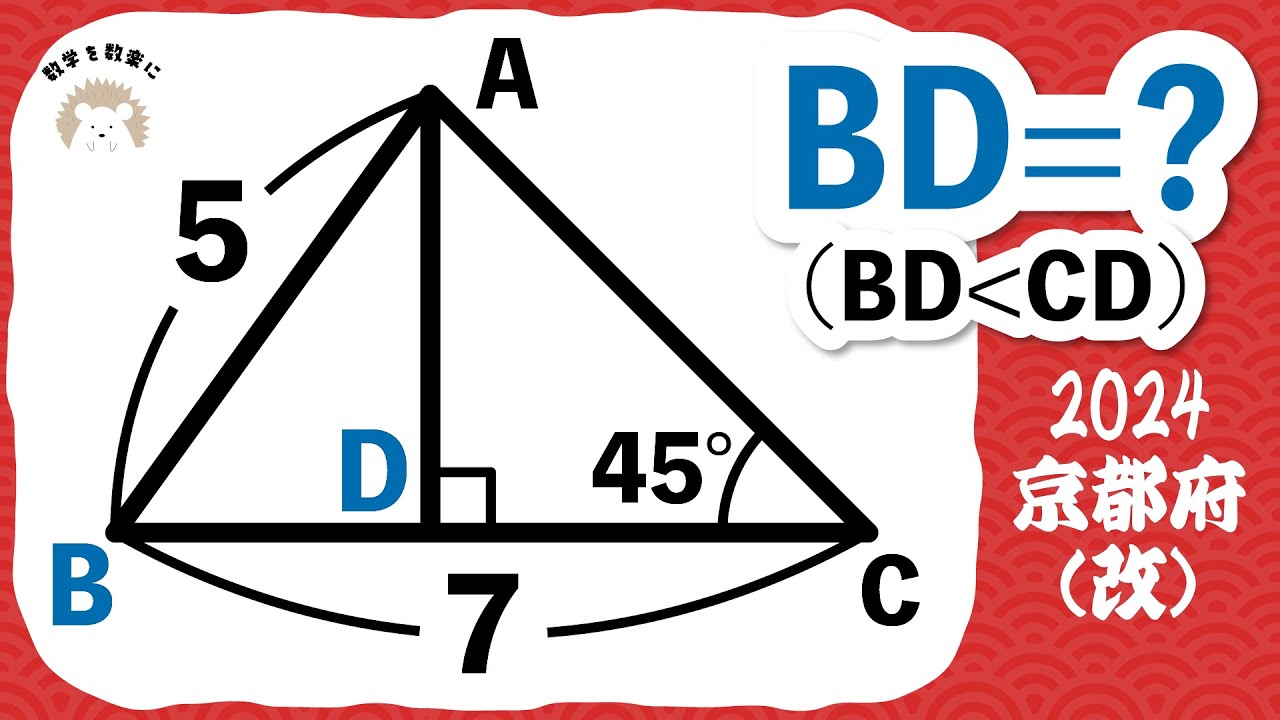
福田のおもしろ数学016〜ジュニア数学オリンピック予選問題〜正三角形の面積
単元：
#算数(中学受験)#数学(中学生)#中１数学#中２数学#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形#三角形と四角形#数学オリンピック
指導講師：
福田次郎
問題文全文(内容文)：
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
この動画を見る
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
【中学数学】2次関数の面積の問題演習～2023年大阪府B問題～【高校受験】
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)#大阪府高等学校
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
右図において, mは関数$y=ax^2$(aは正の定数)のグラフを表し,Iは関数$y=\frac{1}{3}x-1$のグラフを表す。Aは,Iとx軸との交点である。Bは,Aを通りy軸に平行な直線とmとの交点である。
Cは, Bを通りx軸に平行な直線とmとの交点のうちBと異なる点である。
Dは, Cを通りy軸に平行な直線との交点である。
Dは,Cを通りy軸に平行な直線との交点である。
四角形ABCDの面積は21cm²である, aの値を求めなさい。
この動画を見る
右図において, mは関数$y=ax^2$(aは正の定数)のグラフを表し,Iは関数$y=\frac{1}{3}x-1$のグラフを表す。Aは,Iとx軸との交点である。Bは,Aを通りy軸に平行な直線とmとの交点である。
Cは, Bを通りx軸に平行な直線とmとの交点のうちBと異なる点である。
Dは, Cを通りy軸に平行な直線との交点である。
Dは,Cを通りy軸に平行な直線との交点である。
四角形ABCDの面積は21cm²である, aの値を求めなさい。
いろいろな四角形～台形・平行四辺形・ひし形・長方形・正方形～
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説！
この動画を見る
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説！
斜めの正方形は〇〇め！！白陵高校
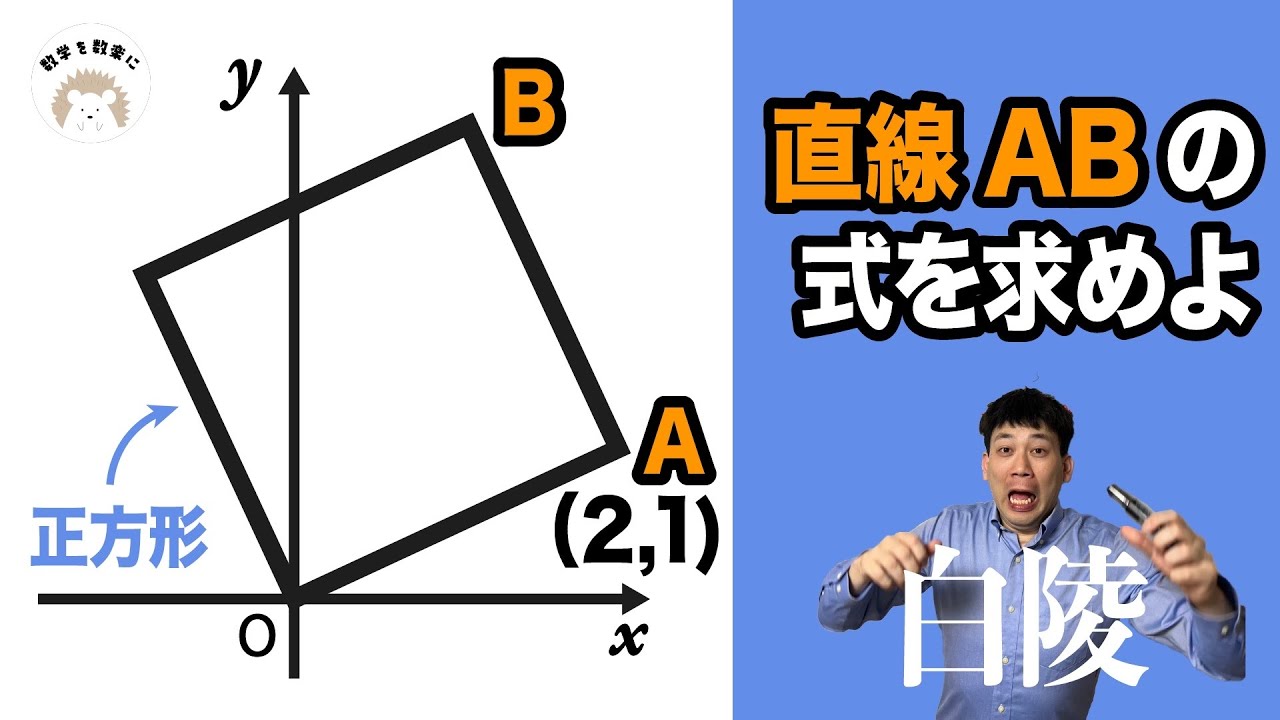
長方形は何こ？
図形問題は補助線が命～全国入試問題解法 #shorts #数学 #mathematics #高校入試 #裏ワザ
単元：
#数学(中学生)#中１数学#空間図形#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
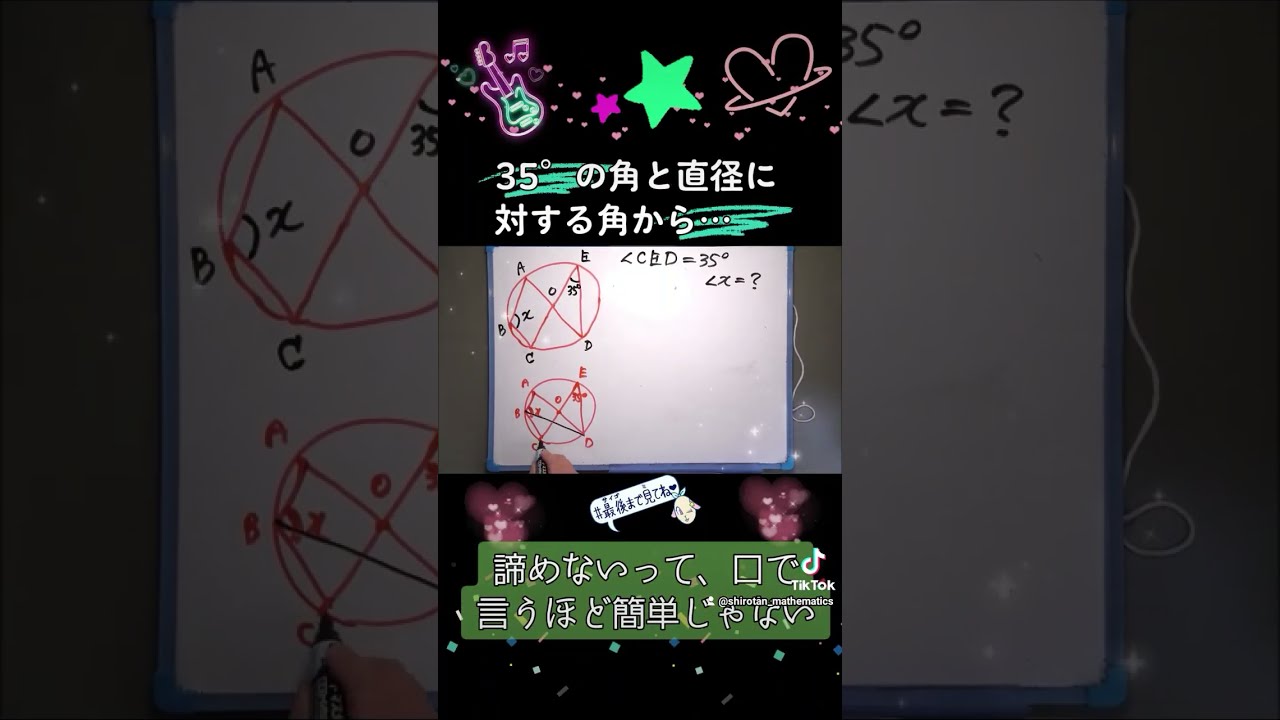
線分AD,CEはともに円Ｏの中心を通る.
$ \angle x$の大きさを求めなさい.
和歌山県高校過去問
この動画を見る
線分AD,CEはともに円Ｏの中心を通る.
$ \angle x$の大きさを求めなさい.
和歌山県高校過去問
図形問題の流れを一発で理解するmovie～全国入試問題解法 #shorts #数学 #math #高校入試
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
図においてxの値を求めなさい.
興南高校過去問
この動画を見る
図においてxの値を求めなさい.
興南高校過去問
何の動画か分かる？
方程式立てずに解ける！ 大阪教育大附属天王寺
単元：
#数学(中学生)#中１数学#文章題#文章題その他#平面図形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは？
大阪教育大学附属高等学校天王寺校舎
この動画を見る
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは？
大阪教育大学附属高等学校天王寺校舎
【中学数学】平面図形の移動～平行移動・回転移動・対称移動～【中１数学】
難解な図形問題を一瞬にして理解するための動画～全国入試問題解法 #shorts #sound #数学 #高校入試
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \angle x $の大きさを求めなさい.
函館白百合学園高校過去問
この動画を見る
$ \angle x $の大きさを求めなさい.
函館白百合学園高校過去問
【2分でコツがつかめる…！】図形：岐阜県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
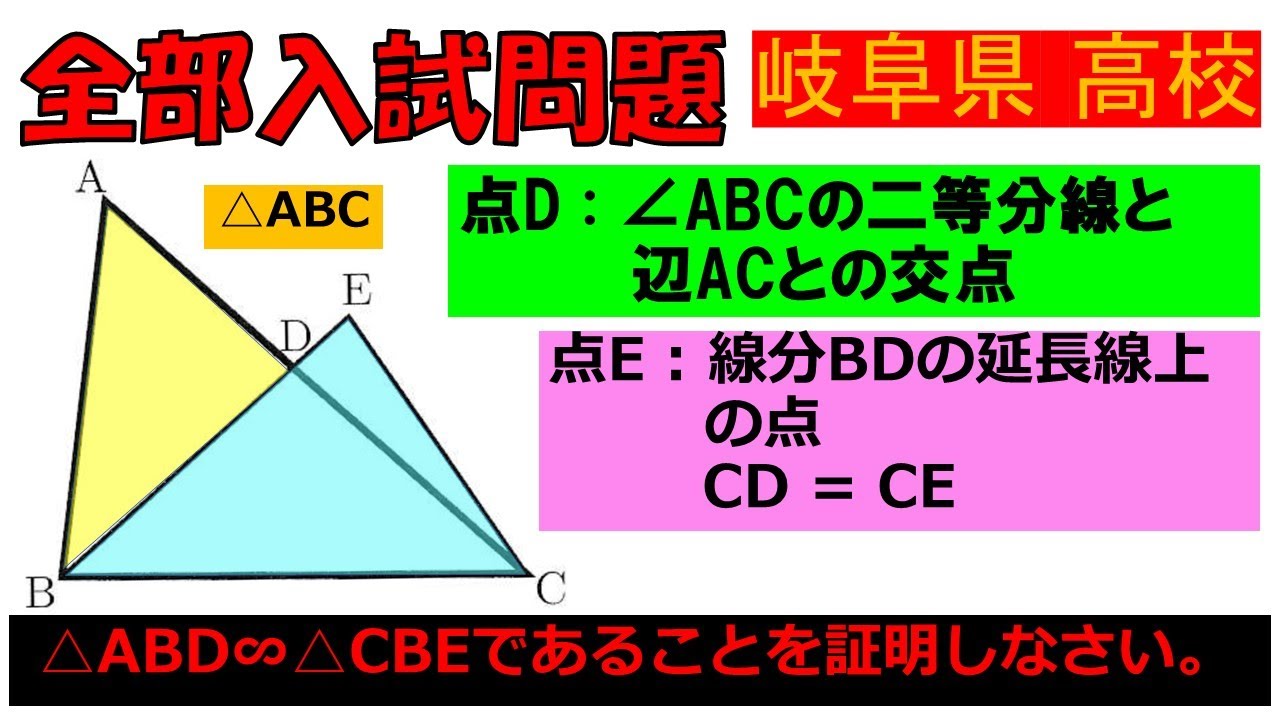
問題文全文(内容文)：
$ \triangle ABD \backsim \triangle CBE $であることを証明しなさい.
岐阜県高校過去問
この動画を見る
$ \triangle ABD \backsim \triangle CBE $であることを証明しなさい.
岐阜県高校過去問
豪華な先生と生徒達 点Pの動く面積＝❓ ラ・サール
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
数学を数楽に
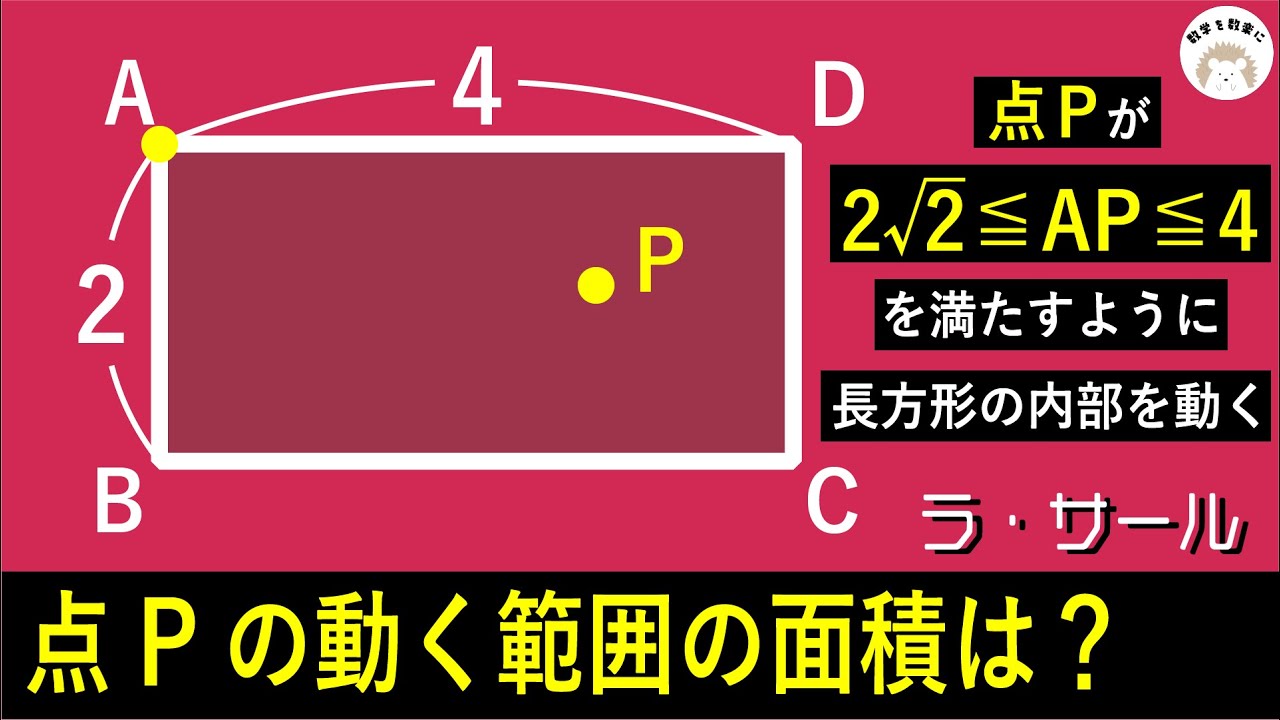
問題文全文(内容文)：
点Pが$2 \sqrt 2 \leqq AP \leqq 4$を満たすように長方形の内部を動く
点Pの動く範囲の面積は？
＊図は動画内参照
ラ・サール学園
この動画を見る
点Pが$2 \sqrt 2 \leqq AP \leqq 4$を満たすように長方形の内部を動く
点Pの動く範囲の面積は？
＊図は動画内参照
ラ・サール学園
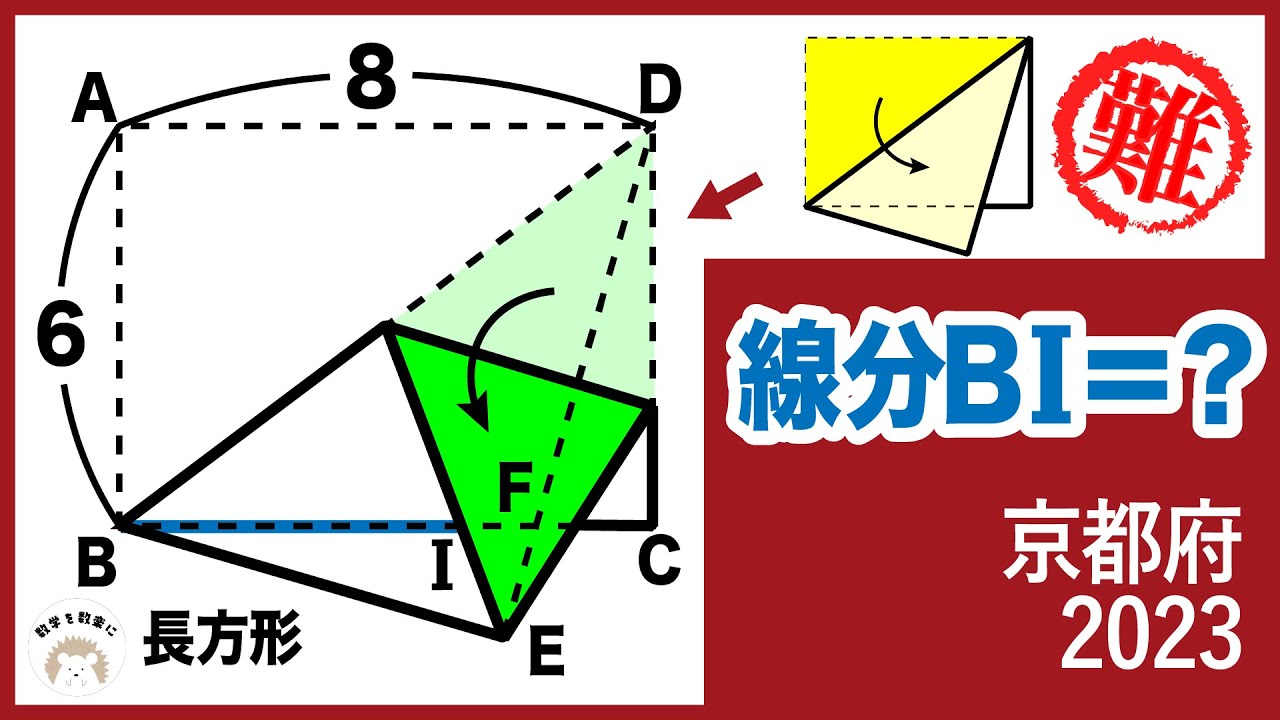
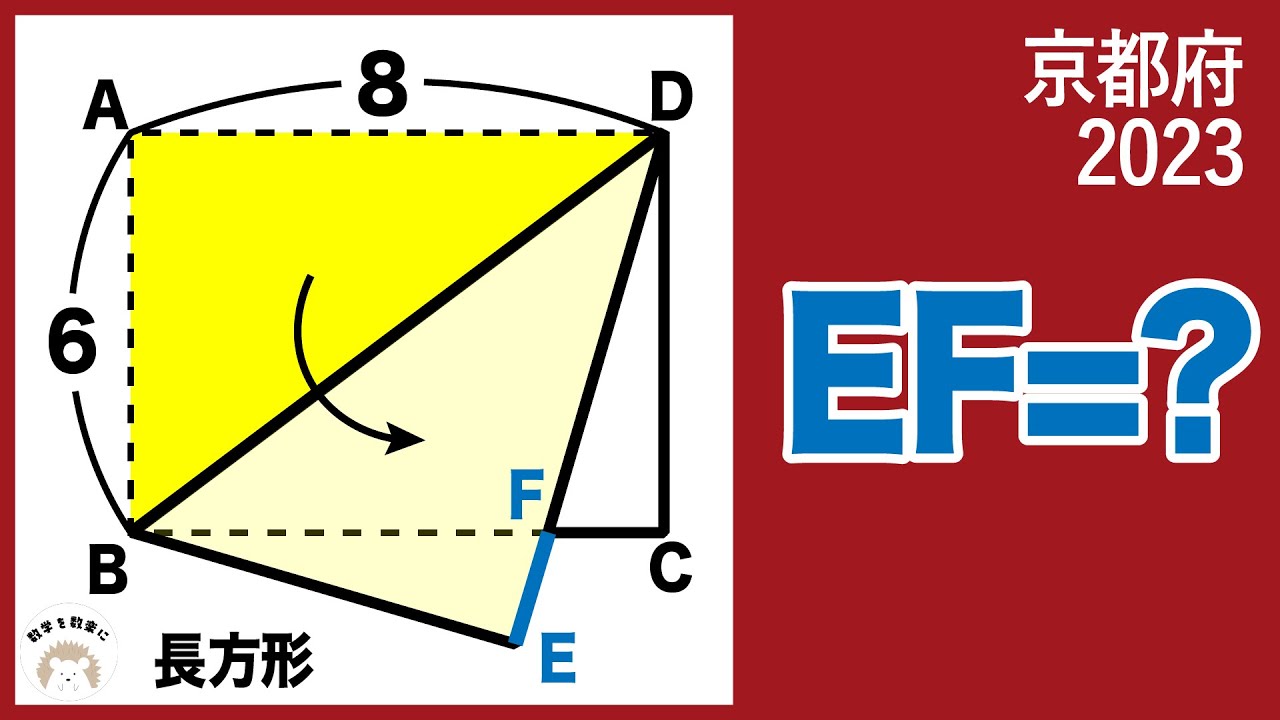
2023高校入試数学解説91問目 長方形の折り返し② 京都府
【中学数学】数学用語チェック絵本 中1の用語”せめて”これだけは覚えよう！！
単元：
#数学(中学生)#中１数学#正の数・負の数#方程式#比例・反比例#空間図形#資料の活用#文字と式#平面図形
指導講師：
理数個別チャンネル
問題文全文(内容文)：
中１で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！vol.1～7の方も見てね♪
この動画を見る
中１で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！vol.1～7の方も見てね♪
2023高校入試数学解説90問目 長方形の折り返し① 京都府
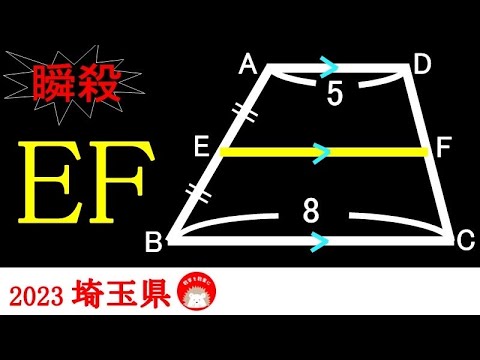
2023高校入試数学解説82問目 気付けば一瞬！！台形 埼玉県
単元：
#数学(中学生)#中１数学#中２数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
EF=?
＊図は動画内参照
2023埼玉県
この動画を見る
EF=?
＊図は動画内参照
2023埼玉県
2023高校入試数学解説76問目 空間上の平面 愛知県
単元：
#数学(中学生)#中１数学#空間図形#平面図形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
空間内の平面について正しく述べたものを全て選べ
ア.異なる2点を含む平面は1つしかない
イ.交わる2直線を含む平面は1つしかない
ウ.平行な2直線を含む平面は1つしかない
エ.同じ直線上にある3点を含む平面は1つしかない
2023愛知県
この動画を見る
空間内の平面について正しく述べたものを全て選べ
ア.異なる2点を含む平面は1つしかない
イ.交わる2直線を含む平面は1つしかない
ウ.平行な2直線を含む平面は1つしかない
エ.同じ直線上にある3点を含む平面は1つしかない
2023愛知県
目盛りをみると答えがわかる 2023高校入試数学解説73問目 東京都
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
△BPQ＝△APB×2
点Pのx座標は？
＊図は動画内参照
2023東京都
この動画を見る
△BPQ＝△APB×2
点Pのx座標は？
＊図は動画内参照
2023東京都
2023高校入試数学解説64問目 小学生も解ける！！角度 城北高校
単元：
#数学(中学生)#中１数学#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
△ABEは正三角形
四角形ABCDは正方形
$\angle AEF =?$
＊図は動画内参照
2023城北学園高等学校
この動画を見る
△ABEは正三角形
四角形ABCDは正方形
$\angle AEF =?$
＊図は動画内参照
2023城北学園高等学校