空間図形
空間図形
本日の一問「図形の性質の証明」【中3数学テスト対策】
単元：
#数学(中学生)#中１数学#中３数学#数A#図形の性質#空間図形#相似な図形#整数の性質#平面図形
指導講師：
いつもの先生
問題文全文(内容文)：
右の図のように、
1辺がPの長さの正方形の池のまわりに、
幅aの道がついている。
この道の面積をS.、道の真ん中を
通る線の長さを$\ell$とすると、
$S=a\ell$となることを証明せよ。
＊図は動画内参照
この動画を見る
右の図のように、
1辺がPの長さの正方形の池のまわりに、
幅aの道がついている。
この道の面積をS.、道の真ん中を
通る線の長さを$\ell$とすると、
$S=a\ell$となることを証明せよ。
＊図は動画内参照
【良問で身に付く数学の応用力！】空間図形：茨城県公立高等学校～全国入試問題解法【とんとん♪】
単元：
#数学(中学生)#空間図形#高校入試過去問(数学)#茨城県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 茨城県の公立高等学校
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
この動画を見る
入試問題 茨城県の公立高等学校
3点A、Q、Rを通る平面で この立方体を切ったとき、
切り口の図形の面積を求めなさい。
点P:辺BF上にある点
点Q:辺EFの中点
点R: FGの中点
※図は動画内参照
「図形のセンス」を身につけよう！
【5分で完全理解！】空間図形：山形県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#空間図形#山形県公立高等学校#山形県立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 山形県の公立高等学校
$OH$の長さを求めなさい。
正四角すい$OABCD :$
$AB=6cm$
点$M$:辺$BC$の中点
$OM=9cm$
四角形$ABCD$の$2$つの対角線 $AC$、$BD$の交点を$H$とする。
※図は動画内参照
この動画を見る
入試問題 山形県の公立高等学校
$OH$の長さを求めなさい。
正四角すい$OABCD :$
$AB=6cm$
点$M$:辺$BC$の中点
$OM=9cm$
四角形$ABCD$の$2$つの対角線 $AC$、$BD$の交点を$H$とする。
※図は動画内参照
【TikTok】円柱の表面積の裏技
【TikTok】円錐の中心角の裏技
立方体の角 A
【5分で完答 !?】空間図形：函館ラ・サール高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#空間図形#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
この動画を見る
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
【中学数学】中学数学で球の体積と表面積の公式の証明
【中学数学】球の公式まとめ～半球とかの裏技も紹介～【中１数学】
2021東京都共通問題の最後の問題 B
単元：
#数学(中学生)#中１数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師：
数学を数楽に
問題文全文(内容文)：
BP＝FQ
D-BPFQの体積=?
＊図は動画内参照
2021東京都
この動画を見る
BP＝FQ
D-BPFQの体積=?
＊図は動画内参照
2021東京都
【中学数学】正多面体の性質～辺，面，頂点の数の求め方～【中１数学】
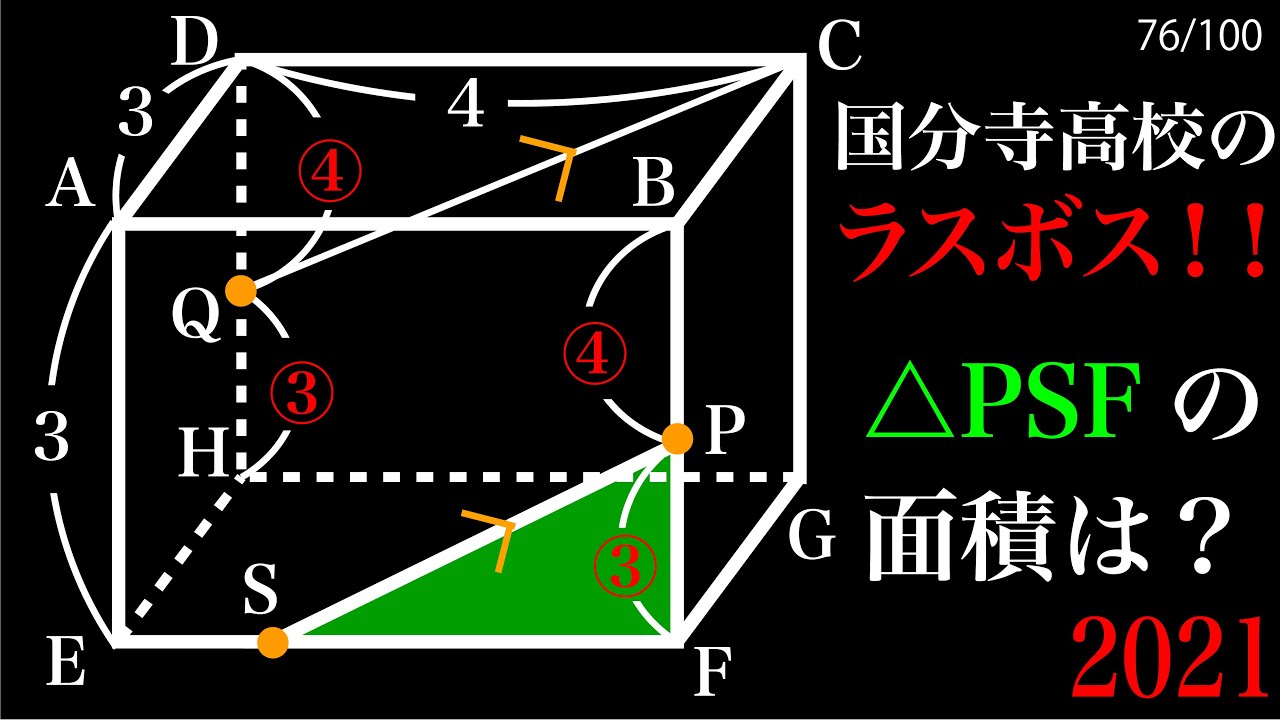
2021 国分寺ラスト問題 B
単元：
#数学(中学生)#中１数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
△PSFの面積=?
＊図は動画内参照
2021国分寺高等学校
この動画を見る
△PSFの面積=?
＊図は動画内参照
2021国分寺高等学校
【中学数学】扇形の中心角の公式～方程式を立てなくても求まる～【中１数学】
空間図形：東京工業大学附属科学技術高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#空間図形#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
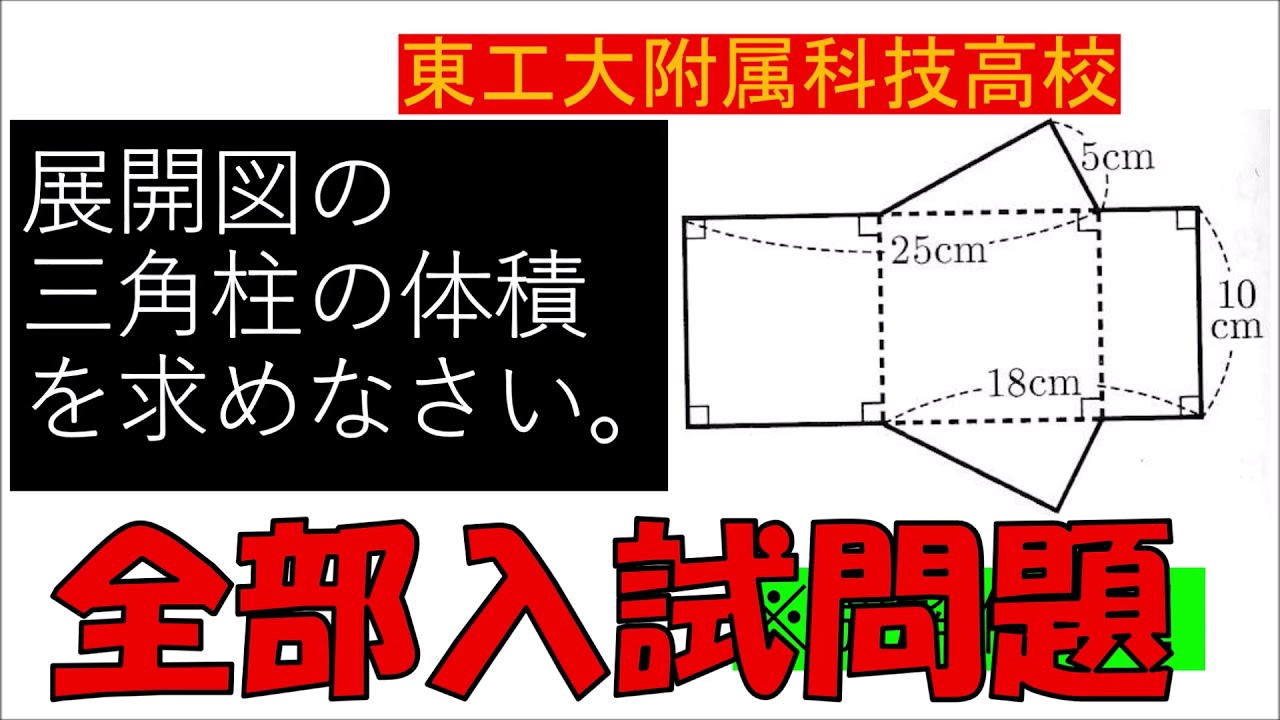
入試問題 東京工業大学附属科学技術高等学校
展開図の 三角柱の体積 を求めなさい。
※別解付き！
※図は動画内参照
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
展開図の 三角柱の体積 を求めなさい。
※別解付き！
※図は動画内参照
【中学数学】円柱の表面積の裏技～使い方と証明～【中１数学】
【中学数学】円錐の裏技集の証明～中心角・側面積・表面積～
【高校受験対策/数学】図形38
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・図形38
Q
図1のように、円すい状のライトが床からの高さ300cmの天井からひもでつり下げられている。
図1の点線は円すいの母線を延長した直線を示しており、ライトから出た光はこの点線の内側を進んで床を円形に照りしているものとする。
図2、図3は天井からつり下げたライトを示したもので、図2のライトAは底面の直径が8cm、高さが10cm、図3のライトBは底面の直径が6cm、高さが10cmの円すいの側面を用いた形状となっている。
①
ライトAをつり下げるひもの長さが100cmのとき、このライトが床を照らしてできる円の直径を求めなさい。
②
ライトをつり下げるひもの長さが$x$cmのときにこのライトが床を照らしてできる円の直径を$y$ cmとする。
$x$の変域を$50 \leqq x \leqq 180$とするとき、$y$を$x$の式で表しなさい。
また、$y$の変域を求めなさい。
③
ライトAとライトBをそれぞれ天井からひもでつり下げて、ひもの長さを変えながら2つのライトが照らしてできる円の面積を調べた。
ライトをつり下げるひもの長さを$x$ cm、ライトBをつり下げるひもの長さを$\frac{x}{2}$ cmとしたとき
2つのライトを照らしてできる円の面積が等しくなるような$x$の値を求めなさい。
この動画を見る
高校受験対策・図形38
Q
図1のように、円すい状のライトが床からの高さ300cmの天井からひもでつり下げられている。
図1の点線は円すいの母線を延長した直線を示しており、ライトから出た光はこの点線の内側を進んで床を円形に照りしているものとする。
図2、図3は天井からつり下げたライトを示したもので、図2のライトAは底面の直径が8cm、高さが10cm、図3のライトBは底面の直径が6cm、高さが10cmの円すいの側面を用いた形状となっている。
①
ライトAをつり下げるひもの長さが100cmのとき、このライトが床を照らしてできる円の直径を求めなさい。
②
ライトをつり下げるひもの長さが$x$cmのときにこのライトが床を照らしてできる円の直径を$y$ cmとする。
$x$の変域を$50 \leqq x \leqq 180$とするとき、$y$を$x$の式で表しなさい。
また、$y$の変域を求めなさい。
③
ライトAとライトBをそれぞれ天井からひもでつり下げて、ひもの長さを変えながら2つのライトが照らしてできる円の面積を調べた。
ライトをつり下げるひもの長さを$x$ cm、ライトBをつり下げるひもの長さを$\frac{x}{2}$ cmとしたとき
2つのライトを照らしてできる円の面積が等しくなるような$x$の値を求めなさい。
【高校受験対策/数学】死守66
単元：
#数学(中学生)#中１数学#中２数学#中３数学#方程式#式の計算（単項式・多項式・式の四則計算）#式の計算（展開、因数分解）#平方根#２次方程式#空間図形#文字と式
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
この動画を見る
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
【高校受験対策/数学】死守64
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#方程式#式の計算（単項式・多項式・式の四則計算）#平方根#空間図形#確率#文字と式#標本調査
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守64
①$\sqrt{26}\div\sqrt{2}$を計算しなさい
➁$2\sqrt{7} \times 3\sqrt{2}$を計算しなさい。
③$5\sqrt{3}+\sqrt{96}-8\sqrt{6}-\sqrt{27}$を計算しなさい。
④$5 \lt \sqrt{a} \leqq 6$を満たす整数$a$の個数を求めなさい。
⑤3点$A(2,1)$、$B(6,-5)$、$C(k,10)$が一直線上にあるとき、$k$の値を求めなさい。
⑥右の表は、あるクラスの女子20人の握力の記録を度数分布表にまとめたものです。
この20人の記録の平均値を求めなさい。
⑦大、小2個のさいころを同時に投げるとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とします。
このとき$\frac{b}{a}$が整数となる確率を求めなさい。
⑧A地点からB地点に行くのに、A地点から途中にあるC地点までは時速$a$ kmで2時間歩き、C地点からB地点までは時速$b$ kmで3時間歩きました。
このとき平均の速さは時速何kmか、$a$、$b$を用いた式で表しなさい。
⑨右の図は、1辺の長さが9cmの立方体から、頂点Aに集まる 3辺 AB、AD、AEをそれぞれ3等分する点のうち、
頂点Aに近い方の3点、P、Q、Rを通る平面で頂点Aを切り取り、同様に頂点B、C、Dも切り取ったものです。
このとき立体の体積は何㎥か求めなさい。
この動画を見る
高校受験対策・死守64
①$\sqrt{26}\div\sqrt{2}$を計算しなさい
➁$2\sqrt{7} \times 3\sqrt{2}$を計算しなさい。
③$5\sqrt{3}+\sqrt{96}-8\sqrt{6}-\sqrt{27}$を計算しなさい。
④$5 \lt \sqrt{a} \leqq 6$を満たす整数$a$の個数を求めなさい。
⑤3点$A(2,1)$、$B(6,-5)$、$C(k,10)$が一直線上にあるとき、$k$の値を求めなさい。
⑥右の表は、あるクラスの女子20人の握力の記録を度数分布表にまとめたものです。
この20人の記録の平均値を求めなさい。
⑦大、小2個のさいころを同時に投げるとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とします。
このとき$\frac{b}{a}$が整数となる確率を求めなさい。
⑧A地点からB地点に行くのに、A地点から途中にあるC地点までは時速$a$ kmで2時間歩き、C地点からB地点までは時速$b$ kmで3時間歩きました。
このとき平均の速さは時速何kmか、$a$、$b$を用いた式で表しなさい。
⑨右の図は、1辺の長さが9cmの立方体から、頂点Aに集まる 3辺 AB、AD、AEをそれぞれ3等分する点のうち、
頂点Aに近い方の3点、P、Q、Rを通る平面で頂点Aを切り取り、同様に頂点B、C、Dも切り取ったものです。
このとき立体の体積は何㎥か求めなさい。
中１数学「円錐の側面の中心角」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第64回円錐の側面の中心角~
例題
ある円錐を展開図に表したら、次の図のように なりました。
(1) 底面の円の半径が9cmのとき、 おうぎ形の中心角は何度ですか。
(2)おうぎ形の中心角が120度のとき、 底面の円の半径は何cmですか。
この動画を見る
中1~第64回円錐の側面の中心角~
例題
ある円錐を展開図に表したら、次の図のように なりました。
(1) 底面の円の半径が9cmのとき、 おうぎ形の中心角は何度ですか。
(2)おうぎ形の中心角が120度のとき、 底面の円の半径は何cmですか。
中１数学「展開図が正方形の三角錐」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第63回展開図が正方形の三角錐
例題
ある立体を展開図に表したら、次の図のように 1辺が6cmの正方形になりました。
(1)この立体の表面積は何cmですか。
(2) この立体の体積は何cmですか。
(3) 面AEFを底面としたときの高さは、 何cmですか。
この動画を見る
中1~第63回展開図が正方形の三角錐
例題
ある立体を展開図に表したら、次の図のように 1辺が6cmの正方形になりました。
(1)この立体の表面積は何cmですか。
(2) この立体の体積は何cmですか。
(3) 面AEFを底面としたときの高さは、 何cmですか。
【高校受験対策/数学】死守62
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#２次方程式#空間図形#文字と式#平面図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア～エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア～エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
中１数学「直線と平面の位置関係」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~直線と平面の位置関係~
例題 次の図は正六角柱です。
(1) 辺AGと平行な面は何面 ありますか。
(2)辺AGと垂直な面は何面 ありますか。
(3) 面ABCDEFと平行な辺は 何本ありますか。
(4)面ABCDEFと垂直な辺は 何本ありますか。
この動画を見る
中1~直線と平面の位置関係~
例題 次の図は正六角柱です。
(1) 辺AGと平行な面は何面 ありますか。
(2)辺AGと垂直な面は何面 ありますか。
(3) 面ABCDEFと平行な辺は 何本ありますか。
(4)面ABCDEFと垂直な辺は 何本ありますか。
中１数学「２直線の位置関係（ねじれ）」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第61回2直線の位置関係~
例題 次の図は正六角柱です。
(1) 辺ABと平行な辺は何本ですか。
(2) 辺ABと垂直な辺は何本ですか。
(3) 辺ABとねじれの位置は何本ですか。
この動画を見る
中1~第61回2直線の位置関係~
例題 次の図は正六角柱です。
(1) 辺ABと平行な辺は何本ですか。
(2) 辺ABと垂直な辺は何本ですか。
(3) 辺ABとねじれの位置は何本ですか。
中１数学「正多面体」【毎日配信】
中１数学「投影図」【毎日配信】
中１数学「回転体」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第58回回転体~
例題
次の図形を直線ℓを回転の軸として、1回転して できる立体の体積と表面積を求めなさい。
この動画を見る
中1~第58回回転体~
例題
次の図形を直線ℓを回転の軸として、1回転して できる立体の体積と表面積を求めなさい。
中１数学「切断した角柱・円柱の体積」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第57回切断した角柱・円柱の体積~
例題 次の図の立体の体積を求めなさい。
この動画を見る
中1~第57回切断した角柱・円柱の体積~
例題 次の図の立体の体積を求めなさい。
中１数学「球の体積と表面積」【毎日配信】
単元：
#数学(中学生)#中１数学#空間図形
指導講師：
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第56回球の体積と表面積~
例1
次の図の球の体積と表面積を求めなさい。
例2
次の図の半球の体積と表面積を求めなさい。
この動画を見る
中1~第56回球の体積と表面積~
例1
次の図の球の体積と表面積を求めなさい。
例2
次の図の半球の体積と表面積を求めなさい。