中１数学
中１数学
【正面突破なら…！】文字式：慶応志木高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#慶應義塾志木高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
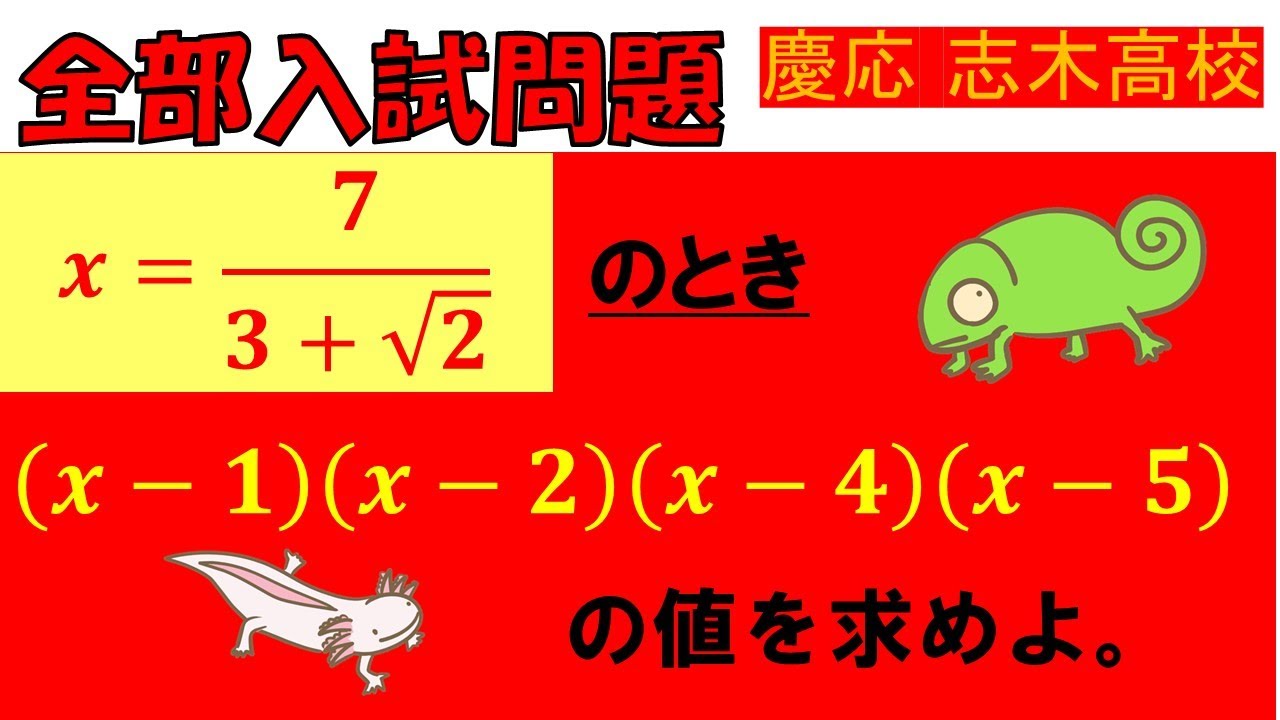
$ x=\dfrac{7}{3+\sqrt2}$のとき,
$ (x-1)(x-2)(x-4)(x-5)$の値を求めよ.
慶応志木高校過去問
この動画を見る
$ x=\dfrac{7}{3+\sqrt2}$のとき,
$ (x-1)(x-2)(x-4)(x-5)$の値を求めよ.
慶応志木高校過去問
文字式は基本を抑えて手際よく！～全国入試問題解法 #shorts #数学 #高校入試 #頭の体操
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
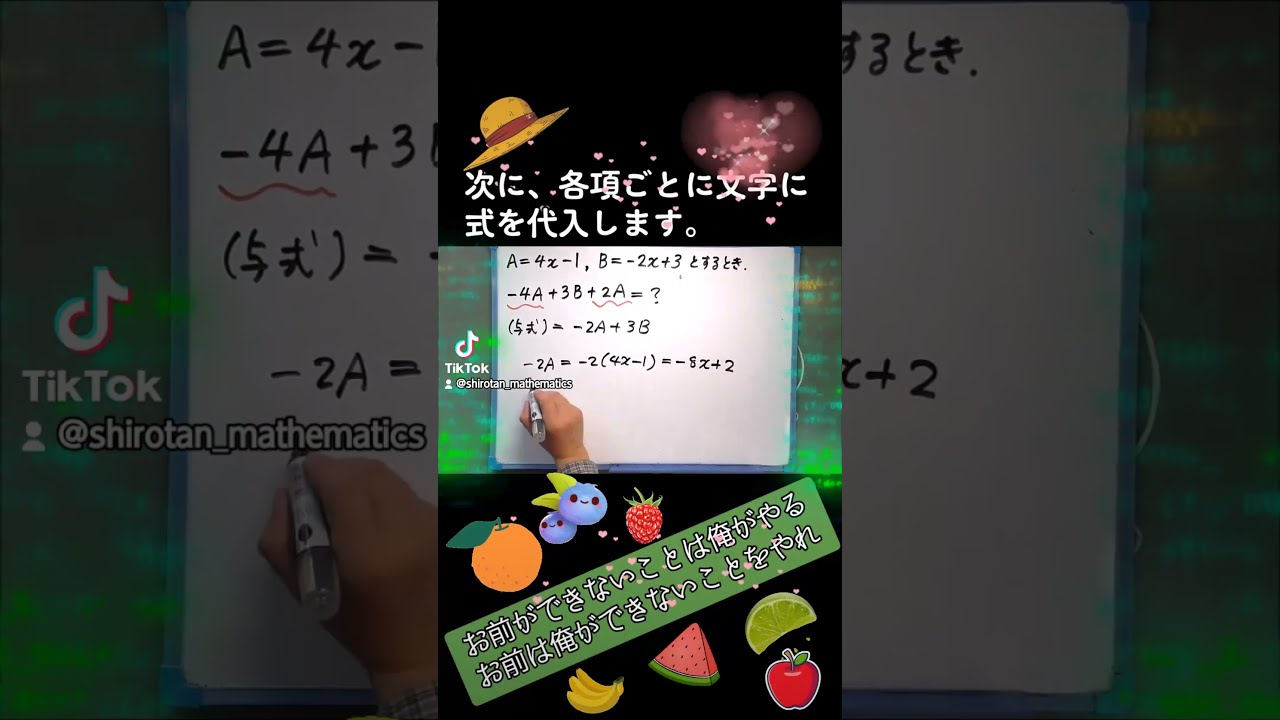
$ A=4x-1 $,$ B=-2x+3 $とするとき,次の計算しなさい.
$ -4A+3B+2A $
滋賀県入試問題過去問
この動画を見る
$ A=4x-1 $,$ B=-2x+3 $とするとき,次の計算しなさい.
$ -4A+3B+2A $
滋賀県入試問題過去問
15秒数で数学の解法！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
3の倍数より1大きい数の2乗から,同じ3の倍数より1小さい数の2乗を
引いた差は,12の倍数である.
この考えがいつでも成り立つことを説明しなさい.
函館白百合学園高校過去問
この動画を見る
3の倍数より1大きい数の2乗から,同じ3の倍数より1小さい数の2乗を
引いた差は,12の倍数である.
この考えがいつでも成り立つことを説明しなさい.
函館白百合学園高校過去問
【良問です！】整数：徳島県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#正の数・負の数#高校入試過去問(数学)#徳島県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
1から9まで9つの自然数から異なる4つの数を選んでその積を
求めると,810になった.
この4つの数をすべて書きなさい.
徳島県公立高等学校過去問
この動画を見る
1から9まで9つの自然数から異なる4つの数を選んでその積を
求めると,810になった.
この4つの数をすべて書きなさい.
徳島県公立高等学校過去問
【学問に王道なし！】整数：福岡大学附属大濠高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
高校入試の文字式の問題を15秒で解説～全国入試問題解法 #shorts #数学 #高校受験 #動体視力 #sound
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\color{red}{ x=4-\sqrt{2022}}$のとき,
$\color{orange}{x^2-8x+15}$の値を求めよ.
関西大倉高校過去問
この動画を見る
$\color{red}{ x=4-\sqrt{2022}}$のとき,
$\color{orange}{x^2-8x+15}$の値を求めよ.
関西大倉高校過去問
【腹をくくって！】有理数：鹿児島県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#正の数・負の数#高校入試過去問(数学)#鹿児島県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \dfrac{9}{11} $
小数で表すとき,$ \color{orange}{小数第20位を求めよ.}$
鹿児島県公立高等学校
この動画を見る
$ \dfrac{9}{11} $
小数で表すとき,$ \color{orange}{小数第20位を求めよ.}$
鹿児島県公立高等学校
【題意を式で表せ！】整数：法政大学高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#方程式#文字と式#高校入試過去問(数学)#法政大学高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \color{red}{整数a}$を$ \color{red}{7}$で割ると$ \color{red}{4}$余り,$ \color{red}{整数b}$を$ \color{red}{7}$で割ると$ \color{red}{3}$余る.
$ \color{orange}{a^2+2ab}$を$ \color{orange}{7}$で割ったときの$ \color{orange}{余り}$を求めなさい.
法政大高校過去問
この動画を見る
$ \color{red}{整数a}$を$ \color{red}{7}$で割ると$ \color{red}{4}$余り,$ \color{red}{整数b}$を$ \color{red}{7}$で割ると$ \color{red}{3}$余る.
$ \color{orange}{a^2+2ab}$を$ \color{orange}{7}$で割ったときの$ \color{orange}{余り}$を求めなさい.
法政大高校過去問
一次方程式の解法を知る15秒！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力
単元：
#数学(中学生)#中１数学#方程式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
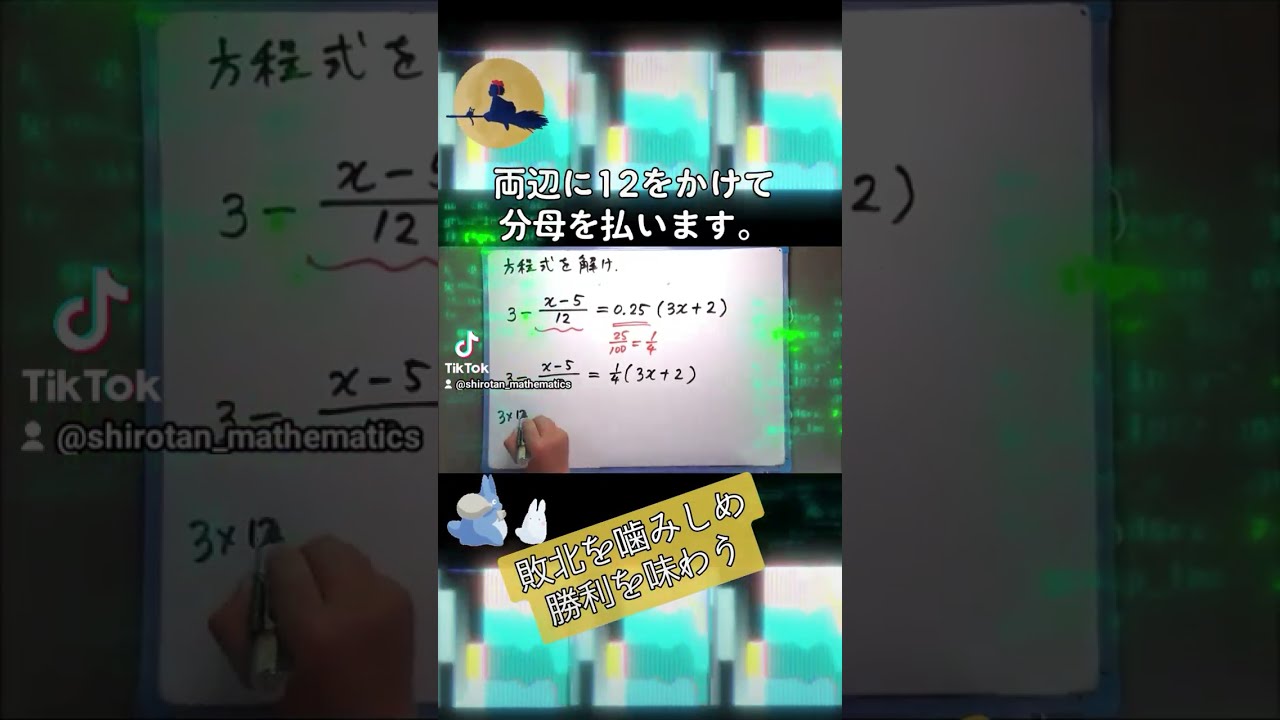
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
この動画を見る
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.
関西大倉高校過去問
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう！！act2まとめ
単元：
#数学(中学生)#中１数学#中２数学#式の計算（単項式・多項式・式の四則計算）#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師：
理数個別チャンネル
問題文全文(内容文)：
中２で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！act2vol.1～7の方も見てね♪
この動画を見る
中２で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ！act2vol.1～7の方も見てね♪
【中学数学】数学用語チェック絵本 act2 vol.7 データの比較
【落ち着いて考えて…！】整数：長崎県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#正の数・負の数#高校入試過去問(数学)#長崎県公立高校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \color{red}{2023}$を割り切ることでできる自然数の中で
$ \color{green}{2023}$の$ \color{orange}{次の大きな自然数}$を求めよ.
長崎県公立高等学校過去問
この動画を見る
$ \color{red}{2023}$を割り切ることでできる自然数の中で
$ \color{green}{2023}$の$ \color{orange}{次の大きな自然数}$を求めよ.
長崎県公立高等学校過去問
15秒であるがままに高校入試の数学～全国入試問題解法 #shorts #数学 #高校入試 #動体視力
単元：
#数学(中学生)#中１数学#方程式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
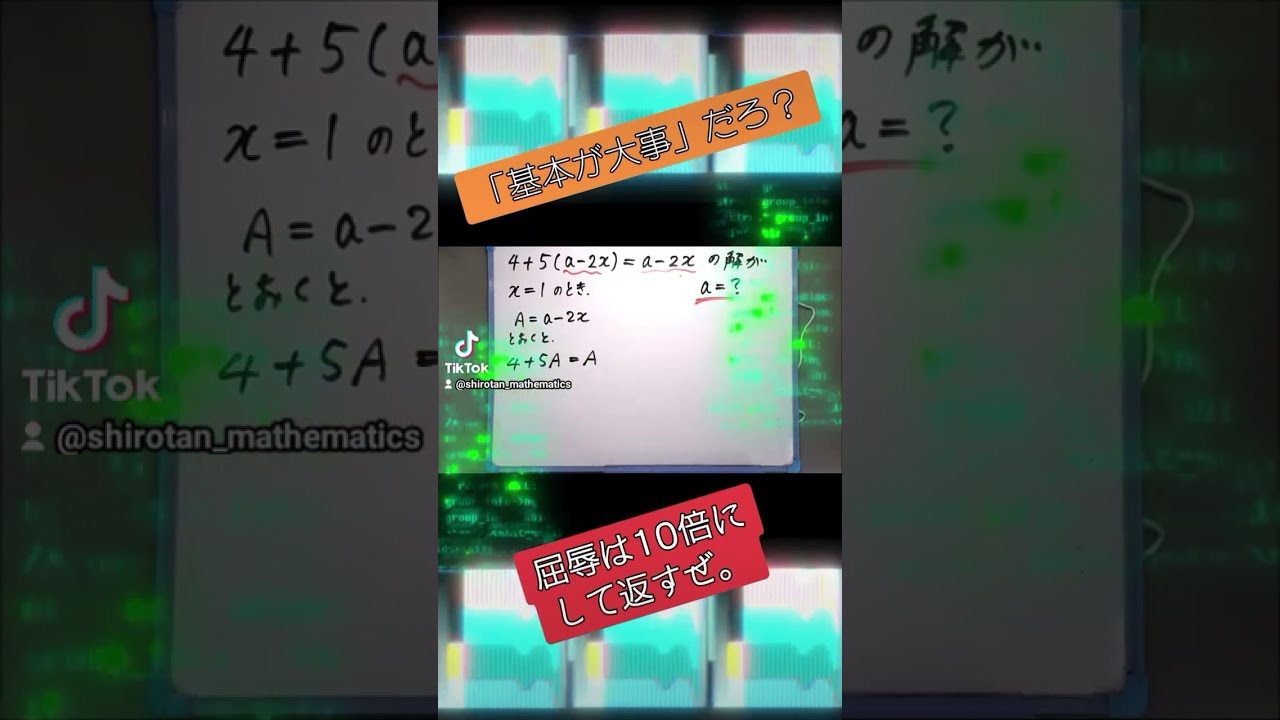
$ 4+5(a-2x)=a-2x $の解が$ x=1 $であるとき,$ a $の値を求めよ.
駿台甲府高校過去問
この動画を見る
$ 4+5(a-2x)=a-2x $の解が$ x=1 $であるとき,$ a $の値を求めよ.
駿台甲府高校過去問
【落ち着いて、そして、素早く！】文字式：奈良県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#奈良県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ a \lt o,b \lt 0 $のとき,
$ a+b,a-b,ab,\dfrac{a}{b}$のうちで,式の値が最も小さいものはどれか.
奈良県公立高等学校過去問
この動画を見る
$ a \lt o,b \lt 0 $のとき,
$ a+b,a-b,ab,\dfrac{a}{b}$のうちで,式の値が最も小さいものはどれか.
奈良県公立高等学校過去問
【やることは分かってる!?】有理数：慶応義塾高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#正の数・負の数#高校入試過去問(数学)#慶應義塾高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \dfrac{3007}{3201}$を既約分数に直すと$ \Box $である.
慶應義塾高校過去問
この動画を見る
$ \dfrac{3007}{3201}$を既約分数に直すと$ \Box $である.
慶應義塾高校過去問
【カギは最初にある！】立体図形：早稲田大学系属早稲田実業学校高等部～全国入試問題解法
単元：
#数学(中学生)#中１数学#空間図形#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
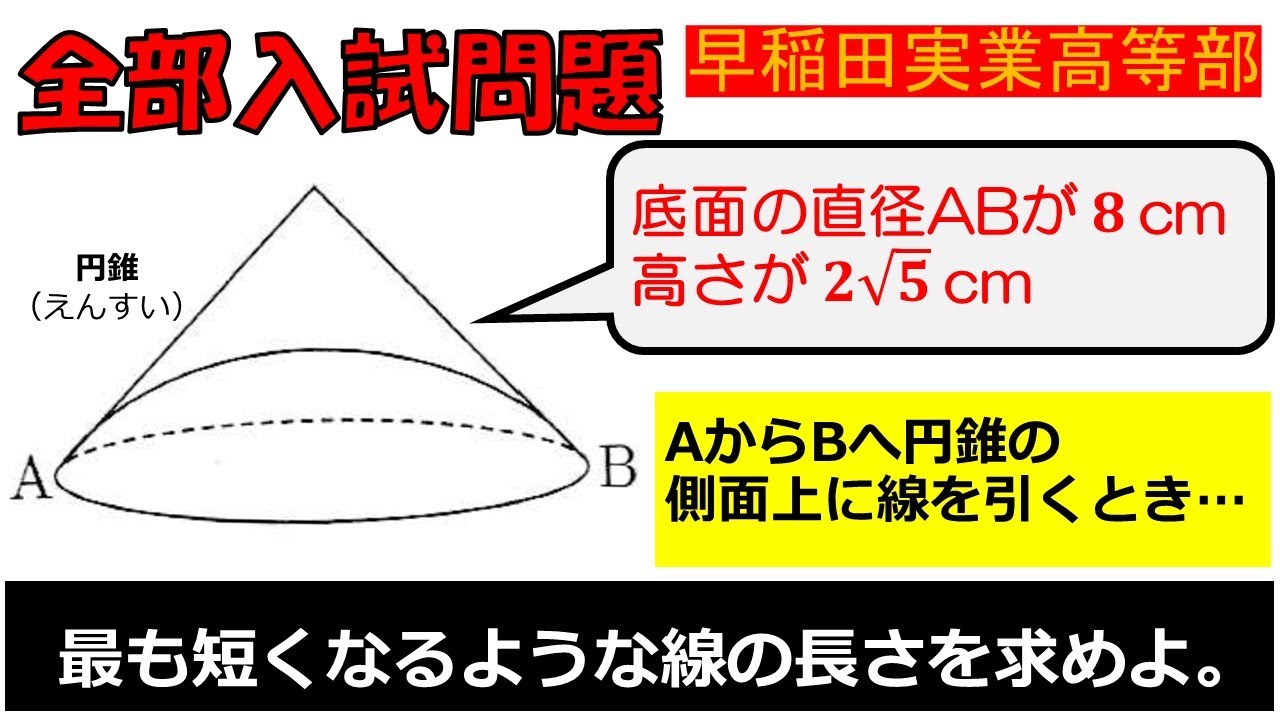
底面の直径$ AB $が8cm、高さが$ 2\sqrt5$cmである.
AからBへ円錐の側面上に線を引くとき,
最も短くなるような線の長さを求めよ.
早稲田実業高等部過去問
この動画を見る
底面の直径$ AB $が8cm、高さが$ 2\sqrt5$cmである.
AからBへ円錐の側面上に線を引くとき,
最も短くなるような線の長さを求めよ.
早稲田実業高等部過去問
数学の文章題を解く流れをつかむ30秒～全国入試問題解法 #shorts #数学 #高校受験 #mathematics
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#精華女子高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
この動画を見る
ある自然数を2乗して3引くところを間違えて2倍して3引いたので,
正しい答えより15小さくなった.ある自然数を求めよ.
精華女子高校過去問
【どちらも大切な解法！】一次関数：新潟県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#中２数学#1次関数#高校入試過去問(数学)#新潟県公立高校入試#新潟県高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
この動画を見る
2点(-1,1),(2,7)を通る直線の式を答えなさい.
新潟県公立高等学校過去問
因数分解の解法の流れをつかむ30秒～全国入試問題解法 #shorts #数学 #高校入試 #mathematics #動体視力 #裏ワザ
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
この動画を見る
$ (x^2+x)^2-x(x+1)-2 $を因数分解しなさい.
明大中野高校過去問
【そこで手を止めない！】因数分解：関西学院高等部～全国入試問題解法
単元：
#数学(中学生)#中１数学#中２数学#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の式を因数分解せよ.
$ (x^2-6x)\times(x^2-6x+17)+72 $
関西学院高等部過去問
この動画を見る
次の式を因数分解せよ.
$ (x^2-6x)\times(x^2-6x+17)+72 $
関西学院高等部過去問
いろいろな四角形～台形・平行四辺形・ひし形・長方形・正方形～
単元：
#数学(中学生)#中１数学#平面図形
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説！
この動画を見る
いろいろな四角形
台形・平行四辺形・ひし形・長方形・正方形についてわかりやすく解説！
【大切な基礎がここにある！】文字式：滋賀県高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#滋賀県公立高校入試#滋賀県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
この動画を見る
$ A=4x-1,B=-2x+3 $とするとき,次の式を計算しなさい.
$ -4A+3B+2A $
滋賀県高等学校過去問
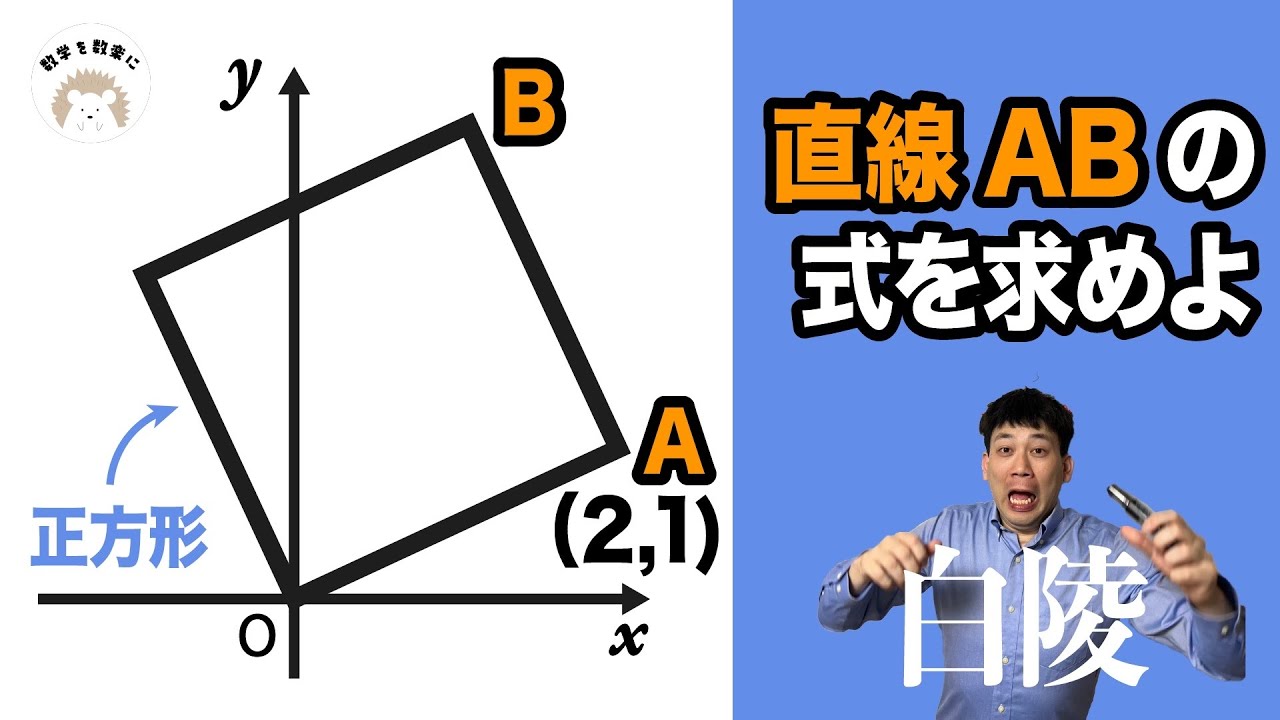
約分して0！
斜めの正方形は〇〇め！！白陵高校
【中学数学】色々な立体と多面体～分かりやすく丁寧に～【中１数学】
帯分数と文字式
1はいちいち書くな
長方形は何こ？
【まず自力で解こう！】文字式：成城学園高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#中３数学#平方根#文字と式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
この動画を見る
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
【考えすぎも悪くない…】文字式：興南高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x+y=-5 $
$ x^2+y^2=17 $
のとき,$ xy $の値を求めなさい.
興南高校過去問
この動画を見る
$ x+y=-5 $
$ x^2+y^2=17 $
のとき,$ xy $の値を求めなさい.
興南高校過去問