 確率
確率
 確率
確率
【食わず嫌いはもったいない!】確率:長野県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#長野県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長野県の高校
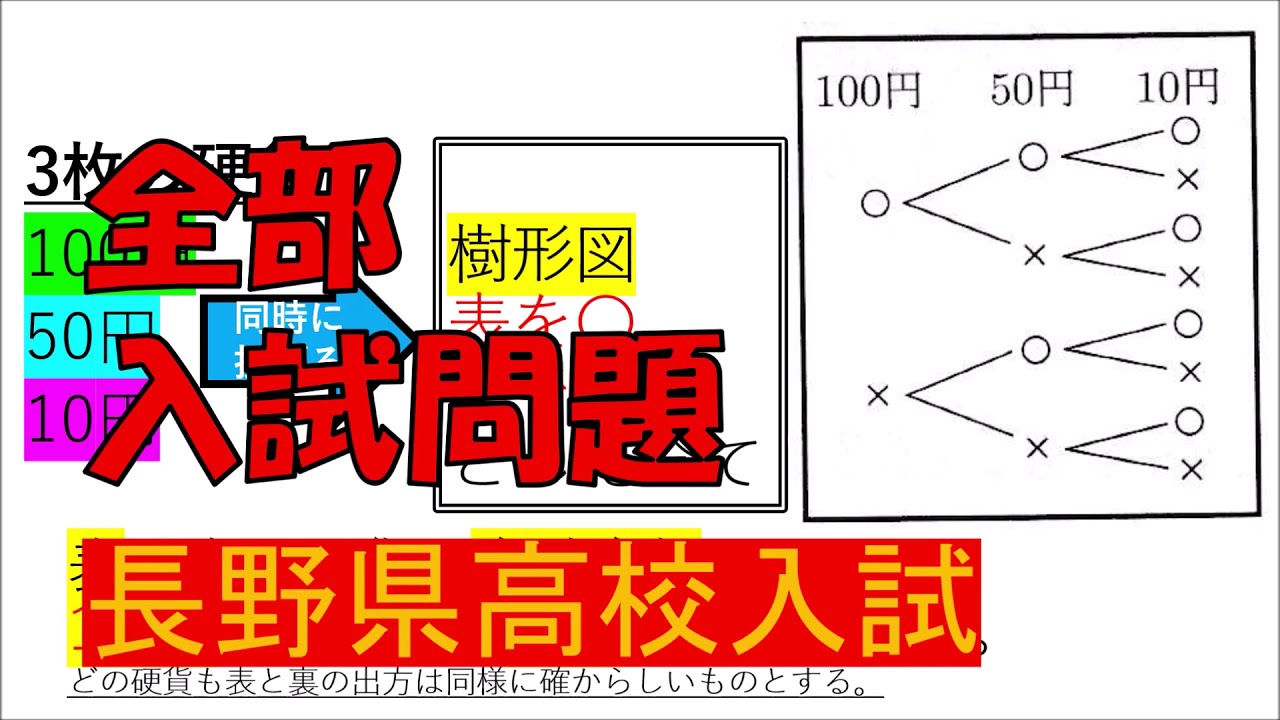
$3$枚の硬貨($100$円、$50$円、$10$円)同時に投げ、
【樹形図】
表を○、 裏を×
とした全て
表が出た硬貨の合計金額が、 $110$円以上になる確率を求めなさい。
どの硬貨も表と裏の出方は同様に確からしいものとする。
※図は動画内参照
この動画を見る
入試問題 長野県の高校
$3$枚の硬貨($100$円、$50$円、$10$円)同時に投げ、
【樹形図】
表を○、 裏を×
とした全て
表が出た硬貨の合計金額が、 $110$円以上になる確率を求めなさい。
どの硬貨も表と裏の出方は同様に確からしいものとする。
※図は動画内参照
【高校受験対策/数学】死守57

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守57
①$6\times (-3)$を計算しなさい。
②$9-(-4)^2 \times \frac{5}{8}$を計算しなさい。
③$a^2b×21b \div 7a$を計算しなさい。
④連立方程式
$0.2x+1.5y=4$
$x-3y=-1$を解きなさい。
⑤$\frac{12}{\sqrt{3}}-3\sqrt{6} \times \sqrt{8}$を計算しなさい。
⑥二次方程式$x^2+5x+5=0$を解きなさい。
⑦ある美術館の入館料は、おとな1人が$a$円、中学生1人が$b$円である。
このとき、不等式$2a+3b \gt 2000$が表している数量の関係として最も適当なものを、次のア~エのうちから1つ選び、符号で答えなさい。
ア おとな2人と中学生3人の入館料の合計は、2000円より安い。
イ おとな2人と中学生3人の入館料の合計は、2000円より高い。
ウ おとな2人と中学生3人の入館料の合計は、2000円以下である。
エ おとな2人と中学生3人の入館料の合計は、2000円以上である。
⑧-5、-2、-1、3、6、10の整数が1つずつ書かれた6枚のカードがある。
この6枚のカードをよくきって、同時に2枚ひく。
このとき、ひいた2枚のカードに書かれた数の平均値が、自然数になる確率を求めなさい。
ただし、どのカードをひくことも同様に確からしいものとする。
この動画を見る
高校受験対策・死守57
①$6\times (-3)$を計算しなさい。
②$9-(-4)^2 \times \frac{5}{8}$を計算しなさい。
③$a^2b×21b \div 7a$を計算しなさい。
④連立方程式
$0.2x+1.5y=4$
$x-3y=-1$を解きなさい。
⑤$\frac{12}{\sqrt{3}}-3\sqrt{6} \times \sqrt{8}$を計算しなさい。
⑥二次方程式$x^2+5x+5=0$を解きなさい。
⑦ある美術館の入館料は、おとな1人が$a$円、中学生1人が$b$円である。
このとき、不等式$2a+3b \gt 2000$が表している数量の関係として最も適当なものを、次のア~エのうちから1つ選び、符号で答えなさい。
ア おとな2人と中学生3人の入館料の合計は、2000円より安い。
イ おとな2人と中学生3人の入館料の合計は、2000円より高い。
ウ おとな2人と中学生3人の入館料の合計は、2000円以下である。
エ おとな2人と中学生3人の入館料の合計は、2000円以上である。
⑧-5、-2、-1、3、6、10の整数が1つずつ書かれた6枚のカードがある。
この6枚のカードをよくきって、同時に2枚ひく。
このとき、ひいた2枚のカードに書かれた数の平均値が、自然数になる確率を求めなさい。
ただし、どのカードをひくことも同様に確からしいものとする。
【数学】40人のグループに同じ誕生日の2人組がいる確率

中学2年生で勉強する確率を1本の動画にまとめてみました。

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
確率のまとめ
ポイント
確率とは(①)が起こると( )される( )を表したもの
〈定期テストではよく出るトランプ〉
Q.ジョーカーを除く52枚のカードから1枚ひくとき、次の確率を求めなさい。
②スペードのカードをひく確率
③ハートかつ奇数のカードをひく確率
この動画を見る
確率のまとめ
ポイント
確率とは(①)が起こると( )される( )を表したもの
〈定期テストではよく出るトランプ〉
Q.ジョーカーを除く52枚のカードから1枚ひくとき、次の確率を求めなさい。
②スペードのカードをひく確率
③ハートかつ奇数のカードをひく確率
【宝くじ】数学的に正しい宝くじの必勝法教えます!宝くじの当選確率ってどれくらい?

【高校受験対策/数学/確率7】シンプルなコイン問題

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
この動画を見る
校受験対策・確率7
Q
表に1と書かれたコインが1枚、2と書かれたコインが1枚、4と書かれたコインが1枚の合計3枚のコインがある。
いずれのコインも裏には何も書かれていない。
この3枚のコインを同時に投げるとき、①②の問いに答えなさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
①表裏の出かたは全部で何通りあるか、求めなさい。
②表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
Q
表に1と書かれたコインが1枚、2と書かれたコインが2枚、4と書かれたコインが1枚の合計4枚のコインが ある。
いずれのコインも裏には何も書かれていない。
この4枚のコインを同時に投げるとき、③、④の問いに答え なさい。
ただし、いずれのコインも表裏の出かたは同様に確からしいものとする。
③表が出たコインに書かれた数の和が、4になる確率を求めなさい。
④表が出たコインに書かれた数の和が、4以上になる確率を求めなさい。
【高校受験対策】数学-死守38

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#連立方程式#2次方程式#1次関数#確率#2次関数#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
【テスト対策 中2】6章-5

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①赤玉2個と白玉4個が入っている袋から、同時に2個取り出すとき、
少なくとも1個が赤玉である確率を求めよ。
②赤玉3個、白玉1個、青玉1個が入っている袋から、同時に2個取り出すとき、
2個の玉の色が異なる確率を求めよ。
③袋Aには赤玉2個と白玉3個、袋Bには赤玉3個と白玉1個が入っている。
それぞれの袋から1個ずつ取り出すとき、異なる色の玉が取り出される確率を求めよ。
この動画を見る
①赤玉2個と白玉4個が入っている袋から、同時に2個取り出すとき、
少なくとも1個が赤玉である確率を求めよ。
②赤玉3個、白玉1個、青玉1個が入っている袋から、同時に2個取り出すとき、
2個の玉の色が異なる確率を求めよ。
③袋Aには赤玉2個と白玉3個、袋Bには赤玉3個と白玉1個が入っている。
それぞれの袋から1個ずつ取り出すとき、異なる色の玉が取り出される確率を求めよ。
【テスト対策 中2】6章-4

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①当たりが3本入った5本のくじがある。
このくじを$A、B$の2人がこの順に1本ずつ引くとき
2人とも当たりを引く確率を求めなさい。
ただし、引いたくじは戻さないものとする。
◎当たりが4本入った10本のくじについて次の問いに答えなさい。
引いたくじは戻さないものとする。
②A君が同時に2本引くとき、2本ともはずれを引く確率を求めなさい。
③A君が同時に2本引き、そのあとにBさんが1本引くとき、
Bさんだけが当たりを引く確率を求めなさい。
この動画を見る
①当たりが3本入った5本のくじがある。
このくじを$A、B$の2人がこの順に1本ずつ引くとき
2人とも当たりを引く確率を求めなさい。
ただし、引いたくじは戻さないものとする。
◎当たりが4本入った10本のくじについて次の問いに答えなさい。
引いたくじは戻さないものとする。
②A君が同時に2本引くとき、2本ともはずれを引く確率を求めなさい。
③A君が同時に2本引き、そのあとにBさんが1本引くとき、
Bさんだけが当たりを引く確率を求めなさい。
【テスト対策 中2】6章-3

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①大小2個のさいころを同時に投げるとき、出る目の数の積が3の倍数になる確率
②大小2個のさいころを同時に投げるとき、少なくとも1個は偶数の目が出る確率
③大中小3個のさいころを同時に投げるとき、少なくとも1個は偶数の目が出る確率
この動画を見る
①大小2個のさいころを同時に投げるとき、出る目の数の積が3の倍数になる確率
②大小2個のさいころを同時に投げるとき、少なくとも1個は偶数の目が出る確率
③大中小3個のさいころを同時に投げるとき、少なくとも1個は偶数の目が出る確率
【テスト対策 中2】6章-2

単元:
#数学(中学生)#中2数学#確率#場合の数#場合の数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$A,B,C,D,E$の5人が1列に並ぶ。
$A$と$B$が端になるようにするとき、並び方は何通りあるか求めなさい。
②さいころ$A$の出る目の数を$a$、さいころ$B$の出る目の数を$b$とする。
$A,B$を同時に投げるとき、$\dfrac{b}{a}$の値が整数になるのは
何通りあるか求めなさい。
この動画を見る
①$A,B,C,D,E$の5人が1列に並ぶ。
$A$と$B$が端になるようにするとき、並び方は何通りあるか求めなさい。
②さいころ$A$の出る目の数を$a$、さいころ$B$の出る目の数を$b$とする。
$A,B$を同時に投げるとき、$\dfrac{b}{a}$の値が整数になるのは
何通りあるか求めなさい。
【テスト対策 中2】6章-1

単元:
#数学(中学生)#中2数学#確率#場合の数#場合の数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$\boxed{1},\boxed{1},\boxed{1},\boxed{2},\boxed{3}$の5枚のカードから2枚取り出して
2桁の整数をつくるとき、 奇数となるのは全部で何通りか求めなさい。
②$\boxed{1},\boxed{1},\boxed{1},\boxed{2},\boxed{3}$の5枚のカードから3枚取り出して
3桁の整数をつくるとき、 奇数となるのは全部で何通りか求めなさい。
図は動画内参照
この動画を見る
①$\boxed{1},\boxed{1},\boxed{1},\boxed{2},\boxed{3}$の5枚のカードから2枚取り出して
2桁の整数をつくるとき、 奇数となるのは全部で何通りか求めなさい。
②$\boxed{1},\boxed{1},\boxed{1},\boxed{2},\boxed{3}$の5枚のカードから3枚取り出して
3桁の整数をつくるとき、 奇数となるのは全部で何通りか求めなさい。
図は動画内参照
【高校受験対策】数学-死守32

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#平行と合同#確率#速さ#速さその他#表とグラフ#表とグラフ・集合
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-2+5$を計算しなさい。
②$3 + 3 ^ 4 \div (- 9)$を計算しなさい。
③$4(2a - 3) - 2(3a - 5)$を計算しなさい。
④$\dfrac{x-y}{6}-\dfrac{x+y}{8}$を計算しなさい。
⑤$3\sqrt8 - \sqrt{50} + sqrt{18}$を計算しなさい。
⑥2次方程式$(x + 2)(x - 2) = 2(3x - 2)$を解きなさい。
⑦かずよしくんは、自宅から1800mはなれた学校に登校するため、
午前7時30分に家を出発した。
最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、
途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。
かずよしくんが走った道のりは何mか、求めなさい。
⑧赤球3個と白球3個が入っている袋がある。
この袋の中から、同時に2個の球を取り出すとき、
赤球と白球が1個ずつである確率を求めなさい。
ただし、どの球を取り出すことも、同様に確からしいものとする。
⑨左下の図1で、正六角形$ABCDEF$に、2つの平行な直線$\ell、m$が交わっており、
交点はそれぞれ$G、H、I、J$である。
$\angle GHF=78°$のとき、$\angle IJE$の大きさを求めなさい。
⑩ある中学校の1年A組25人と1年B組25人の休日の学習時間を調べた。
下の図2、 図3は、それぞれの結果をヒストグラムに表したもので、
2つの図から「1年A組は1年B組 より、$\Box$」と読みとることができた。
$\Box$にあてはまるものとして適切なものを、 下のア~エから1つ選び、記号で書きなさい。
ア→学習時間の分布の範囲が小さい
イ→最頻値を含む階級の度数が多い
ウ→中央値を含む、階級の度数が少ない
エ→学習時間が150分以上の人数が多い
図は動画内参照
この動画を見る
①$-2+5$を計算しなさい。
②$3 + 3 ^ 4 \div (- 9)$を計算しなさい。
③$4(2a - 3) - 2(3a - 5)$を計算しなさい。
④$\dfrac{x-y}{6}-\dfrac{x+y}{8}$を計算しなさい。
⑤$3\sqrt8 - \sqrt{50} + sqrt{18}$を計算しなさい。
⑥2次方程式$(x + 2)(x - 2) = 2(3x - 2)$を解きなさい。
⑦かずよしくんは、自宅から1800mはなれた学校に登校するため、
午前7時30分に家を出発した。
最初は毎分60mの速さで歩いていたが、遅刻しそうになったので、
途中から毎分100mの速さで走ったところ、午前7時56分に学校に着いた。
かずよしくんが走った道のりは何mか、求めなさい。
⑧赤球3個と白球3個が入っている袋がある。
この袋の中から、同時に2個の球を取り出すとき、
赤球と白球が1個ずつである確率を求めなさい。
ただし、どの球を取り出すことも、同様に確からしいものとする。
⑨左下の図1で、正六角形$ABCDEF$に、2つの平行な直線$\ell、m$が交わっており、
交点はそれぞれ$G、H、I、J$である。
$\angle GHF=78°$のとき、$\angle IJE$の大きさを求めなさい。
⑩ある中学校の1年A組25人と1年B組25人の休日の学習時間を調べた。
下の図2、 図3は、それぞれの結果をヒストグラムに表したもので、
2つの図から「1年A組は1年B組 より、$\Box$」と読みとることができた。
$\Box$にあてはまるものとして適切なものを、 下のア~エから1つ選び、記号で書きなさい。
ア→学習時間の分布の範囲が小さい
イ→最頻値を含む階級の度数が多い
ウ→中央値を含む、階級の度数が少ない
エ→学習時間が150分以上の人数が多い
図は動画内参照
【高校受験対策】数学-死守31

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#確率#2次関数#表とグラフ#表とグラフ・集合
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
この動画を見る
①$13 + 3\times (- 6)$を計算せよ。
②$3(2a + 3) - 2(5a + 4)$ を計算せよ。
③$a = - 3 , b = 4$とき、$3a^2-5b$の値を求めよ。
④$\dfrac{30}{\sqrt5}+\sqrt{20}$を計算せよ。
⑤ 1次方程式$3x-8=7x+16$を解け。
⑥2次方程式$(x + 1) ^ 2 = x + 13$を解け。
⑦関数$y =\dfrac{2}{3}x^2$について、
$x$の変域が$-1\leqq x \leqq 3$のときの$y$の変域を求めよ。
⑧$\boxed{1},\boxed{3},\boxed{5},\boxed{7},\boxed{9}$のカードが1枚ずつある。
この5枚のカードから、同時に2枚のカードを取り出すとき、
その2枚のカードにかかれている数の和が10以上になる確率を求めよ。
ただし、どのカードを取り出すことも同様に確からしいものとする。
⑨右の表は、A中学校とB中学校の生徒を対象に、
携帯電話やスマートフォンの1日あたりの使用時間を調査し、
その結果を度数分布表に整理したものである。
この表をもとに、A中学校とB中学校の「0時間以上1時間未満」の階級の相対度数のうち、
大きい方の相対度数を四捨五入して小数第2位まで求めよ。
図は動画内参照
【高校受験対策】数学-確率5

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎右の図のような、1辺が2の正方形$ABCD$があり、頂点$D$に点$P$、頂点$A$に
点$Q$がある。
赤と白の2個のさいころを同時に1回投げて、
赤いさいころの出た目の数だけ$P$を左回りに頂点から頂点へ移動させ、
白いさいころの出た目の数だけ$Q$を左回りに頂点から頂点へ移動させる。
たとえば、赤いさいころの出た目が1、白いさいころの出た目が2のときは、
$P$を$D→A$、$Q$を$A→B→C$と移動させる。
このとき、次の問に答えなさい。
①赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$P$の位置が頂点$B$で、$Q$の位置が頂点$D$になる確率を求めなさい。
②赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$△APQ$の面積が2になる確率を求めなさい。
③表1のように、各頂点の点数を決め、$P、Q$の移動後の位置に応じてそれぞれ点数を与える。
赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$P$の点数が$Q$の点数より高くなる確率を求めなさい。
図は動画内参照
この動画を見る
◎右の図のような、1辺が2の正方形$ABCD$があり、頂点$D$に点$P$、頂点$A$に
点$Q$がある。
赤と白の2個のさいころを同時に1回投げて、
赤いさいころの出た目の数だけ$P$を左回りに頂点から頂点へ移動させ、
白いさいころの出た目の数だけ$Q$を左回りに頂点から頂点へ移動させる。
たとえば、赤いさいころの出た目が1、白いさいころの出た目が2のときは、
$P$を$D→A$、$Q$を$A→B→C$と移動させる。
このとき、次の問に答えなさい。
①赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$P$の位置が頂点$B$で、$Q$の位置が頂点$D$になる確率を求めなさい。
②赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$△APQ$の面積が2になる確率を求めなさい。
③表1のように、各頂点の点数を決め、$P、Q$の移動後の位置に応じてそれぞれ点数を与える。
赤と白の2個のさいころを同時に1回投げて、$P、Q$を移動させるとき、
$P$の点数が$Q$の点数より高くなる確率を求めなさい。
図は動画内参照
【高校受験対策】数学-死守28

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#2次関数#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
この動画を見る
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
【高校受験対策】数学-死守26

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#数と式#確率#円#一次不等式(不等式・絶対値のある方程式・不等式)#文章題#文章題その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
この動画を見る
①$-3+8$を計算しなさい.
②$2(2x - y) - (x - y)$を計算しなさい.
③$\sqrt{27}-\sqrt{63}$を計算しなさい.
④$(x + 5)(x - 3)$を展開しなさい.
⑤$a(b + 8) - (b + 8)$を因数分解しなさい.
⑥2次方程式 $x ^ 2 + x = 3$を解きなさい.
⑦右の図1の円$O$において,
$\angle x$と$\angle y$の大きさをそれぞれ求めなさい.
⑧鉛筆1本の値段を$a$円,ノート1冊の値段を$b$円とする.
「鉛筆3本とノート1冊の代金を払うと,
300円でおつりがもらえた」という数量の関係を,
不等式で表しなさい.ただし,値段は税込みとする.
⑨箱の中に,25本の当たりを含むたくさんのくじが入っている.
このくじをよくかき混ぜた後,48人がこの箱から1人1回ずつくじを引いたところ,
当たりが2本出た.箱の中に最初に入っていたくじの本数は,
およそ何本であったと推定できるか,求めなさい.
⑩ある水族館の入館料は,おとな3人と子ども2人で入ると4020円かかり,
おとな1人と子ども3人で入ると2600円かかる.
おとな1人,子ども1人の入館料をそれぞれ求めなさい.
ただし,入館料は税込みとする.
図は動画内参照
【高校受験対策】数学-死守23

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#2次方程式#確率#立体図形#立体切断#立体図形その他#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
この動画を見る
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
【高校受験対策】数学-死守22

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#立体図形#立体切断#立体図形その他
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$1-(-3)$を計算しなさい.
②$2a+\dfrac{a}{3}$を計算しなさい.
③$4(2x - y) - 3(x + y) $を計算しなさい.
④$(3x+1)^2$展開しなさい.
⑤$4a^2-12ab$を因数分解しなさい.
⑥連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=4 \\
4x-3y=18
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦七角形の内角の和を求めなさい.
⑧2次方程式$x ^ 2 + x - 12 = 0$を解きなさい.
⑨$\sqrt2 \lt x \lt \sqrt{19}$を満たす$x$を,小さい順にすべて書きなさい.
⑩右の図は,立体図の展開図である.
この展開図を組み立てて立方体をつくるとき,
面アと垂直になる面を,面イ~カからすべて選び,記号で答えなさい.
⑪$1,2,3,4,5$の数字を1つずつ記入した5枚のカードがある.
このカードをよくきってから1枚ずつ2回続けて引き,
引いた順に左から並べて2けたの整数をつくる.
このとき,できた2けたの整数が4の倍数である確率を求めなさい.
図は動画内参照
この動画を見る
①$1-(-3)$を計算しなさい.
②$2a+\dfrac{a}{3}$を計算しなさい.
③$4(2x - y) - 3(x + y) $を計算しなさい.
④$(3x+1)^2$展開しなさい.
⑤$4a^2-12ab$を因数分解しなさい.
⑥連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=4 \\
4x-3y=18
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦七角形の内角の和を求めなさい.
⑧2次方程式$x ^ 2 + x - 12 = 0$を解きなさい.
⑨$\sqrt2 \lt x \lt \sqrt{19}$を満たす$x$を,小さい順にすべて書きなさい.
⑩右の図は,立体図の展開図である.
この展開図を組み立てて立方体をつくるとき,
面アと垂直になる面を,面イ~カからすべて選び,記号で答えなさい.
⑪$1,2,3,4,5$の数字を1つずつ記入した5枚のカードがある.
このカードをよくきってから1枚ずつ2回続けて引き,
引いた順に左から並べて2けたの整数をつくる.
このとき,できた2けたの整数が4の倍数である確率を求めなさい.
図は動画内参照
【高校受験対策】数学-死守20

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#数と式#比例・反比例#確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
この動画を見る
①$(-2)+11$を計算しなさい.
②$(- 4) ^ 2 \times (- 3)$を計算しなさい.
③$(6a - 15b) \div 3$を計算しなさい.
④$(2x - 1)(x + 3)$を展開しなさい.
⑤$x ^ 2 - (y + 3) ^ 2$ を因数分解しなさい.
⑥方程式$\dfrac{x - 2}{4} + \dfrac{2 - 5x}{6} = 1$を解きなさい.
⑦$y$は$x$に反比例し,$x = 2$ のとき $y = - 3$ である.
このとき,$y$を$x$の式で表しなさい.
⑧次のア~オの中から,無理数をすべて選び,記号で答えなさい.
ア.$\dfrac{1}{3}$
イ.$\sqrt5$
ウ.$0.25$
エ.$-2\sqrt3$
オ.$\sqrt6$
⑨右の図のア~エは,関数$y = ax ^ 2$のグラフである.
次の(1),(2)の問いに答えなさい.
(1)関数$y=\dfrac{1}{2}x^2$のグラフを,ア~エから選びなさい.
(2)$x$の値が$-2$から$-1$まで増加するときの
変化の割合が最も大きい関数のグラフを,ア~エから選びなさい.
また,そのときの変化の割合を求めなさい.
⑩袋の中に$0,1,2,3$の数字が1つずつ書かれた4個の玉が入っている.
この袋から玉を1個取り出して玉に書かれた数字を確認して,
それを袋の中にもどしてから,また1個取り出すとき,
(1)取り出した2個の玉に書かれていた数字が同じになる確率を求めなさい.
(2)次の$\Box$に適することばを入れて,
求める確率が$\dfrac{1}{4}$となる問題を1つ完成させなさい.
「取り出した2個の玉の数字の積が$\Box$になる確率を求めなさい.」
図は動画内参照
【高校受験対策】数学-死守19

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#2次方程式#比例・反比例#確率#文章題#文章題その他#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$8-(-13)$を計算しなさい.
②$(- 3) ^ 2 + \left(-\dfrac{1}{3}\right)\times 6$ を計算しなさい.
③$(7a - 4b) + \dfrac{1}{2}(2b - 6a)$ を計算しなさい.
④方程式$ 0.2(x - 2) = x + 1.2$ を解きなさい.
⑤$\sqrt{48}-\sqrt{27}+5\sqrt3$を計算しなさい.
⑥二次方程式$x ^ 2 + 7x + 5 = 0 $を解きなさい.
⑦$y$は$x$の2乗に比例し,
$ x = 2 $のとき,$y=1$である.
$y$を$x$の式で表しなさい.
⑧右の資料は,ある生徒が受けた第1回から第6回までの数学のテストの得点の記録のうち,
第1回から第5回までの得点の記録である.
第1回から第6回までの得点の中央値が80点となるとき,
第6回のテストの得点を求めなさい.
$\boxed{83 \quad 78\quad 74\quad 77 \quad 96}$ (単位:点)
⑨$m$と$n$は連続する正の整数である.
次のア~エのうちから,次の値が偶数となるものを一つ選び,
符号で答えなさい.ただし,$m \lt n$とする.
ア.$m+n$
イ.$n-m$
ウ.m + n + 2$
エ.$mn$
⑩箱の中に同じ大きさの白い球だけがたくさん入っている.
この白い球が何個あるか,標本調査を行って推測しょうと考えた.
そこでオレンジ色の球200個を箱に入れてよくかき混ぜ,
そこから50個を無作為に抽出したところ,
オレンジ色の球が4個含まれていた.
はじめに箱の中に入っていた白い球の個数を推測しなさい
①箱の中に$②,③,④,⑥,⑧,⑨$のカードがそれぞれ1枚ずつ入っている.
この箱から同時に2枚取り出すとき,
取り出した2枚のカードに書かれた数の最小公倍数が,
1桁の数になる確率を求めなさい.
ただし,どのカードの取り出し方も同様に確からしいものとする.
この動画を見る
①$8-(-13)$を計算しなさい.
②$(- 3) ^ 2 + \left(-\dfrac{1}{3}\right)\times 6$ を計算しなさい.
③$(7a - 4b) + \dfrac{1}{2}(2b - 6a)$ を計算しなさい.
④方程式$ 0.2(x - 2) = x + 1.2$ を解きなさい.
⑤$\sqrt{48}-\sqrt{27}+5\sqrt3$を計算しなさい.
⑥二次方程式$x ^ 2 + 7x + 5 = 0 $を解きなさい.
⑦$y$は$x$の2乗に比例し,
$ x = 2 $のとき,$y=1$である.
$y$を$x$の式で表しなさい.
⑧右の資料は,ある生徒が受けた第1回から第6回までの数学のテストの得点の記録のうち,
第1回から第5回までの得点の記録である.
第1回から第6回までの得点の中央値が80点となるとき,
第6回のテストの得点を求めなさい.
$\boxed{83 \quad 78\quad 74\quad 77 \quad 96}$ (単位:点)
⑨$m$と$n$は連続する正の整数である.
次のア~エのうちから,次の値が偶数となるものを一つ選び,
符号で答えなさい.ただし,$m \lt n$とする.
ア.$m+n$
イ.$n-m$
ウ.m + n + 2$
エ.$mn$
⑩箱の中に同じ大きさの白い球だけがたくさん入っている.
この白い球が何個あるか,標本調査を行って推測しょうと考えた.
そこでオレンジ色の球200個を箱に入れてよくかき混ぜ,
そこから50個を無作為に抽出したところ,
オレンジ色の球が4個含まれていた.
はじめに箱の中に入っていた白い球の個数を推測しなさい
①箱の中に$②,③,④,⑥,⑧,⑨$のカードがそれぞれ1枚ずつ入っている.
この箱から同時に2枚取り出すとき,
取り出した2枚のカードに書かれた数の最小公倍数が,
1桁の数になる確率を求めなさい.
ただし,どのカードの取り出し方も同様に確からしいものとする.
【高校受験対策】数学-死守18

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#2次方程式#比例・反比例#確率#点と直線
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問いに答えなさい.
①$15 - 9\div 3$を計算しなさい.
②$\dfrac{2}{7}\times \dfrac{3}{4}$を計算しなさい .
③$-5-3+7$を計算しなさい.
④$(3x - 2y) + 5(x - 4y)$ を計算しなさい.
⑤$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=2 \\
x+2y=-6
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
⑦$\sqrt{15}\times \sqrt6 +\sqrt{10}$を計算しなさい.
⑧$x^2-2x-63$を因数分解しなさい.
⑧方程式$ 2x ^ 2 + 9x + 8 = 0$ を解きなさい.
⑨右の図のように,平行な2直線$\ell,m$があり,直線上に2点$A,B$
直線$m$上に2点$C,D$がある.
$AB=BC, \angle BCD = 42°$のとき,$\angle BAC$の大きさを求めなさい.
⑩下の表は,$y$が$x$に反比例する関係を表したものです.
表のⒶにあてはまる数を求めなさい.
⑪数字を書いた3枚のカード$①,②,③$が袋$A$の中に,
数字を書いた5枚のカード$①,②,③,④,⑤$が袋$B$の中に入っています.
それぞれの袋からカードを1枚ずつ取り出すとき,
その2枚のカードに書いてある数の積が奇数になる確率を求めなさい.
図は動画内参照
この動画を見る
次の各問いに答えなさい.
①$15 - 9\div 3$を計算しなさい.
②$\dfrac{2}{7}\times \dfrac{3}{4}$を計算しなさい .
③$-5-3+7$を計算しなさい.
④$(3x - 2y) + 5(x - 4y)$ を計算しなさい.
⑤$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=2 \\
x+2y=-6
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
⑦$\sqrt{15}\times \sqrt6 +\sqrt{10}$を計算しなさい.
⑧$x^2-2x-63$を因数分解しなさい.
⑧方程式$ 2x ^ 2 + 9x + 8 = 0$ を解きなさい.
⑨右の図のように,平行な2直線$\ell,m$があり,直線上に2点$A,B$
直線$m$上に2点$C,D$がある.
$AB=BC, \angle BCD = 42°$のとき,$\angle BAC$の大きさを求めなさい.
⑩下の表は,$y$が$x$に反比例する関係を表したものです.
表のⒶにあてはまる数を求めなさい.
⑪数字を書いた3枚のカード$①,②,③$が袋$A$の中に,
数字を書いた5枚のカード$①,②,③,④,⑤$が袋$B$の中に入っています.
それぞれの袋からカードを1枚ずつ取り出すとき,
その2枚のカードに書いてある数の積が奇数になる確率を求めなさい.
図は動画内参照
【高校受験対策】数学-死守17

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#確率#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問いに答えなさい.
①$6-2\times (-5)$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{7}{9}$を計算しなさい.
③$2(a+3b)-(a-4b)$を計算しなさい.
④$\sqrt8+\dfrac{6}{\sqrt2}$を計算しなさい.
⑤2次方程式$x^2+2x-15=0$を計算しなさい.
⑥赤,白,青の棒が各1本ずつ箱の中に入っている.
この3本の棒をよく混ぜて1本取り出し,色を確認してからもとにもどします.
このことを2回行うとき,確認した色が2回とも赤か,
2回とも白になる確率を求めなさい.
⑦相似な2つの立体$P,Q$があり,その表面積の比は$4:9$です.
立体$P$の体積が$8cm^3$のとき,立体$Q$の体積を求めなさい.
⑧図1のように,関数$y = ax^2$グラフ上に,$x$座標が-1となる点をとります.
また,$x$軸上の,座標が$ (1,0)$となる点を$B$とします.
直線$AB$の切片が2のとき,$a$の値を求めなさい.
⑨図2のように,直線$\ell$,2点$A,B$があります.
直線$\ell$上にあって,2点$A,B$から等しい距離にある点$P$を,
作図によって求めなさい.
なお,作図に用いた線は消さずに残しなさい.
図は動画内参照
この動画を見る
次の各問いに答えなさい.
①$6-2\times (-5)$を計算しなさい.
②$\dfrac{1}{3}-\dfrac{7}{9}$を計算しなさい.
③$2(a+3b)-(a-4b)$を計算しなさい.
④$\sqrt8+\dfrac{6}{\sqrt2}$を計算しなさい.
⑤2次方程式$x^2+2x-15=0$を計算しなさい.
⑥赤,白,青の棒が各1本ずつ箱の中に入っている.
この3本の棒をよく混ぜて1本取り出し,色を確認してからもとにもどします.
このことを2回行うとき,確認した色が2回とも赤か,
2回とも白になる確率を求めなさい.
⑦相似な2つの立体$P,Q$があり,その表面積の比は$4:9$です.
立体$P$の体積が$8cm^3$のとき,立体$Q$の体積を求めなさい.
⑧図1のように,関数$y = ax^2$グラフ上に,$x$座標が-1となる点をとります.
また,$x$軸上の,座標が$ (1,0)$となる点を$B$とします.
直線$AB$の切片が2のとき,$a$の値を求めなさい.
⑨図2のように,直線$\ell$,2点$A,B$があります.
直線$\ell$上にあって,2点$A,B$から等しい距離にある点$P$を,
作図によって求めなさい.
なお,作図に用いた線は消さずに残しなさい.
図は動画内参照
【高校受験対策】数学-死守16

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#確率#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問いに答えなさい.
①$-4+(-3)$を計算しなさい.
②$-\dfrac{1}{7}+\dfrac{2}{5}$を計算しなさい.
③$16ab^2 \div 8ab$を計算しなさい.
④$\sqrt{54}-\dfrac{42}{\sqrt6}$を計算しなさい.
⑤$(x+2)(x+3)-(x+4)^2$を計算しなさい.
⑥$(x-5)^2-7(x-5)+12$を因数分解しなさい.
⑦2次方程式$5x^2-3x-1=0$を解きなさい.
⑧$x=3-\sqrt7$のとき,
$x^2-6x+9$の値を求めなさい.
⑨関数$y=ax^2$について,
$x$の値が$-3$から$-1$まで増加するときの変化の割合が$-3$であった.
このとき,$a$の値を求めなさい.
⑩1から6までの目の出る大,小2つのさいころを同時に1回投げるとき,
出た目の数の和が9以上とならない確率を求めなさい.
⑪半径が$2cm$である球の体積を$Pcm^3$,l
半径が$3cm$である球の体積を$Qcm^3$とするとき,
$P$と$Q$の比を最も簡単な整数の比で表しなさい。.
ただし,円周率は$\pi$とする.
⑫ 右の図において,線分$AB$は円$O$の直径であり,
2点$C,D$は円$O$の周上の点である.
このとき,$△ABC$の大きさを求めなさい.
この動画を見る
次の各問いに答えなさい.
①$-4+(-3)$を計算しなさい.
②$-\dfrac{1}{7}+\dfrac{2}{5}$を計算しなさい.
③$16ab^2 \div 8ab$を計算しなさい.
④$\sqrt{54}-\dfrac{42}{\sqrt6}$を計算しなさい.
⑤$(x+2)(x+3)-(x+4)^2$を計算しなさい.
⑥$(x-5)^2-7(x-5)+12$を因数分解しなさい.
⑦2次方程式$5x^2-3x-1=0$を解きなさい.
⑧$x=3-\sqrt7$のとき,
$x^2-6x+9$の値を求めなさい.
⑨関数$y=ax^2$について,
$x$の値が$-3$から$-1$まで増加するときの変化の割合が$-3$であった.
このとき,$a$の値を求めなさい.
⑩1から6までの目の出る大,小2つのさいころを同時に1回投げるとき,
出た目の数の和が9以上とならない確率を求めなさい.
⑪半径が$2cm$である球の体積を$Pcm^3$,l
半径が$3cm$である球の体積を$Qcm^3$とするとき,
$P$と$Q$の比を最も簡単な整数の比で表しなさい。.
ただし,円周率は$\pi$とする.
⑫ 右の図において,線分$AB$は円$O$の直径であり,
2点$C,D$は円$O$の周上の点である.
このとき,$△ABC$の大きさを求めなさい.
【高校受験対策】数学-死守15

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#確率#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問に答えなさい.
①$6x-x$を計算しなさい.
②$6+(-2)\times 4$を計算しなさい.
③$\sqrt{45}-2\sqrt5$を計算しなさい.
④$x=18$のとき,
$x^2-6x-16$の値を求めなさい.
⑤2次方程式$3x^2+7x+1=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=18 \\
x+y=7
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦関数$y=\dfrac{1}{2}x^2$の値が1から5まで増加するときの変化の割合が,
一次関数$y = ax + 2$ の変化の割合と等しくなりました.
$a$の値を求めなさい.
⑧図1のような円錐の形のチョコレートがあります.
このチョコレートの8分の1の量をもらえることになり,
底面と平行に切って頂点のあるほうをもらうことにしました.
母線の長さを$8cm$とすると,
頂点から母線にそって何$cm$のところを切ればよいかを求めなさい.
⑨図2で,$\angle A=48$の$△ABC$があり,$\angle B,\angle C$の
二等分線をそれぞれかいたときの交点を$D$とします.
このとき,$\angle BDC$の大きさを求めなさい.
➉図3のように,円周上に18個の点が等間隔に並んでおり,
そのうちの点を$P$とします.
1個の黒石を点$P$上に置き,この黒石を,
1から6までの目が出るさいころを1回投げるごとに,
出た目の数だけ円周上の点上を順に動かします.
動かし方は,偶数の目が出たときは右回りに,
奇数の目が出たときは左回りに動かすものとします.
さいころを3回投げたとき,黒石が点$P$に戻っている確率を求めなさい.
図は動画内を参照
この動画を見る
次の各問に答えなさい.
①$6x-x$を計算しなさい.
②$6+(-2)\times 4$を計算しなさい.
③$\sqrt{45}-2\sqrt5$を計算しなさい.
④$x=18$のとき,
$x^2-6x-16$の値を求めなさい.
⑤2次方程式$3x^2+7x+1=0$を解きなさい.
⑥連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=18 \\
x+y=7
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑦関数$y=\dfrac{1}{2}x^2$の値が1から5まで増加するときの変化の割合が,
一次関数$y = ax + 2$ の変化の割合と等しくなりました.
$a$の値を求めなさい.
⑧図1のような円錐の形のチョコレートがあります.
このチョコレートの8分の1の量をもらえることになり,
底面と平行に切って頂点のあるほうをもらうことにしました.
母線の長さを$8cm$とすると,
頂点から母線にそって何$cm$のところを切ればよいかを求めなさい.
⑨図2で,$\angle A=48$の$△ABC$があり,$\angle B,\angle C$の
二等分線をそれぞれかいたときの交点を$D$とします.
このとき,$\angle BDC$の大きさを求めなさい.
➉図3のように,円周上に18個の点が等間隔に並んでおり,
そのうちの点を$P$とします.
1個の黒石を点$P$上に置き,この黒石を,
1から6までの目が出るさいころを1回投げるごとに,
出た目の数だけ円周上の点上を順に動かします.
動かし方は,偶数の目が出たときは右回りに,
奇数の目が出たときは左回りに動かすものとします.
さいころを3回投げたとき,黒石が点$P$に戻っている確率を求めなさい.
図は動画内を参照
【高校受験対策】数学-死守13

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#確率#円#立体図形#立体図形その他#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の各問いに答えなさい.
①$3-(-2)$を計算しなさい.
②$(-3)^2+5\times (-1)$を計算しなさい.
③$(2x^2-5x)-(3x^2-2x)$を計算しなさい.
④$(-4a^2)\times 18b \div 9ab$を計算しなさい.
⑤$(\sqrt3 + 1)^2$を計算しなさい.
⑥$x$に$-3$をかけて$5$をひいた数は$7$より小さい.
この数量の関係を不等式で表しなさい.
⑦次の連立方程式を解きなさい.
$3x+4y=x+y=2$
⑧2次方程式$(x-2)^2=81$を解きなさい.
⑨右の図で,$y$が$x$に比例するとき,
(ア)にあてはまる数を求めなさい.
⑩$1,2,3,4$の数字が書かれた4枚のカードが袋の中に入っている.
このカードを2枚同時に取り出すとき,
袋の中に残っているカードに書かれている数の和が,
取り出したカードに書かれている数の和より大きくなる確率を求めなさい.
⑪右上の図1は,底面の半径が$6cm$,母線の長さが$30cm$の円すいである.
この円すいの展開図をかいたとき,側面になるおうぎ形の中心角を求めなさい.
⑫右の図2の平行四辺形$ABCD$で,
$AB,BC$上にそれぞれ点$E,F$をとる.
$AC /\!/ EF$のとき,$△ACE$と面積が等しい三角形を3つ書きなさい.
図は動画内を参照
この動画を見る
次の各問いに答えなさい.
①$3-(-2)$を計算しなさい.
②$(-3)^2+5\times (-1)$を計算しなさい.
③$(2x^2-5x)-(3x^2-2x)$を計算しなさい.
④$(-4a^2)\times 18b \div 9ab$を計算しなさい.
⑤$(\sqrt3 + 1)^2$を計算しなさい.
⑥$x$に$-3$をかけて$5$をひいた数は$7$より小さい.
この数量の関係を不等式で表しなさい.
⑦次の連立方程式を解きなさい.
$3x+4y=x+y=2$
⑧2次方程式$(x-2)^2=81$を解きなさい.
⑨右の図で,$y$が$x$に比例するとき,
(ア)にあてはまる数を求めなさい.
⑩$1,2,3,4$の数字が書かれた4枚のカードが袋の中に入っている.
このカードを2枚同時に取り出すとき,
袋の中に残っているカードに書かれている数の和が,
取り出したカードに書かれている数の和より大きくなる確率を求めなさい.
⑪右上の図1は,底面の半径が$6cm$,母線の長さが$30cm$の円すいである.
この円すいの展開図をかいたとき,側面になるおうぎ形の中心角を求めなさい.
⑫右の図2の平行四辺形$ABCD$で,
$AB,BC$上にそれぞれ点$E,F$をとる.
$AC /\!/ EF$のとき,$△ACE$と面積が等しい三角形を3つ書きなさい.
図は動画内を参照
【高校受験対策】数学-死守12

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の問いに答えよ.
①$5 \times (-4)^2 -3^2$を計算せよ.
②$\dfrac{5x-3y}{3}-\dfrac{3x-7y}{4}$を計算せよ.
③$\sqrt{27}-\dfrac{12}{\sqrt 3}-\sqrt{75}$を計算せよ.
④$x=\sqrt7+2,y=\sqrt7-2$のとき,
$x^2-y^2$の値を求めよ.
⑤方程式$2x+3y+6=0$のグラフをかけ.
⑥2次方程式$(x-2)^2=6$を解け.
⑦$1,2,4,8,16,32$の数が書かれた棒が1本ずつ入っている箱がある.
この箱から棒を同時に2本取り出すとき,
2本の棒に書かれている数の和が3の倍数となる確率を求めよ.
ただし,どの棒の取り出し方も同様に確からしいものとする.
⑧箱の中に白い玉だけがたくさん入っている.
この箱に赤い玉を80個入れてよくかき混ぜ,箱から50個の玉を無作為に取り出すと,
赤い玉が9個含まれていた.
最初に箱の中に入っていた白い玉はおよそ何個であると推測されるか,
次の(ア)~(エ)から1つ選べ.
(ア)およそ320個
(イ)およそ360個
(ウ)およそ400個
(エ)およそ440個
図は動画内を参照
この動画を見る
次の問いに答えよ.
①$5 \times (-4)^2 -3^2$を計算せよ.
②$\dfrac{5x-3y}{3}-\dfrac{3x-7y}{4}$を計算せよ.
③$\sqrt{27}-\dfrac{12}{\sqrt 3}-\sqrt{75}$を計算せよ.
④$x=\sqrt7+2,y=\sqrt7-2$のとき,
$x^2-y^2$の値を求めよ.
⑤方程式$2x+3y+6=0$のグラフをかけ.
⑥2次方程式$(x-2)^2=6$を解け.
⑦$1,2,4,8,16,32$の数が書かれた棒が1本ずつ入っている箱がある.
この箱から棒を同時に2本取り出すとき,
2本の棒に書かれている数の和が3の倍数となる確率を求めよ.
ただし,どの棒の取り出し方も同様に確からしいものとする.
⑧箱の中に白い玉だけがたくさん入っている.
この箱に赤い玉を80個入れてよくかき混ぜ,箱から50個の玉を無作為に取り出すと,
赤い玉が9個含まれていた.
最初に箱の中に入っていた白い玉はおよそ何個であると推測されるか,
次の(ア)~(エ)から1つ選べ.
(ア)およそ320個
(イ)およそ360個
(ウ)およそ400個
(エ)およそ440個
図は動画内を参照
【高校受験対策】数学-死守7

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#確率#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1.次の計算をしなさい.
①$4+(-9)$
②$2-3\times (-2)$
③$3ab-ab$
2.次の各問に答えなさい.
④次の$\Box$に当てはまる記号を,
$=,<,>$の中から選びなさい.
$(-6)^2\Box -6^2$
⑤$(x+2y)(x-2y)$を展開しなさい.
⑥$x^2+2x-8$を因数分解しなさい.
⑦$x=\sqrt2,y=(\sqrt3 -\sqrt2)$のとき,
$x^2+xy$の値を求めなさい.
⑧方程式$\dfrac{1}{2}x+3=2x$を解きなさい.
⑨連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x + y = 8 \\
x - 3y =15
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑩右の図で,点$A,B,C,D$は円$O$の周上の点で,
$\angle ADB=36°$,線分$AC$は円$O$の直径である.
このとき,$\angle BAC$の大きさを求めなさい.
⑪1つのさいころを2回投げるとき,
2回目に出た目の数が,1回目に出た目の数の約数となる
確率を求めなさい.
図は動画内を参照
この動画を見る
1.次の計算をしなさい.
①$4+(-9)$
②$2-3\times (-2)$
③$3ab-ab$
2.次の各問に答えなさい.
④次の$\Box$に当てはまる記号を,
$=,<,>$の中から選びなさい.
$(-6)^2\Box -6^2$
⑤$(x+2y)(x-2y)$を展開しなさい.
⑥$x^2+2x-8$を因数分解しなさい.
⑦$x=\sqrt2,y=(\sqrt3 -\sqrt2)$のとき,
$x^2+xy$の値を求めなさい.
⑧方程式$\dfrac{1}{2}x+3=2x$を解きなさい.
⑨連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x + y = 8 \\
x - 3y =15
\end{array}
\right.
\end{eqnarray}$を解きなさい.
⑩右の図で,点$A,B,C,D$は円$O$の周上の点で,
$\angle ADB=36°$,線分$AC$は円$O$の直径である.
このとき,$\angle BAC$の大きさを求めなさい.
⑪1つのさいころを2回投げるとき,
2回目に出た目の数が,1回目に出た目の数の約数となる
確率を求めなさい.
図は動画内を参照
【高校受験対策】数学-確率4

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
下の図は,$\boxed{A},\boxed{B},\boxed{C},\boxed{D}$の4種類のカードを,
1列に並べたものです. 大小2つのさいころを同時に1回投げます.
大きい方のさいころの出た目の数を入として,
左から$x$番目のカードとそれより左にあるすべてのカードを列から取り除きます.
また,小さい方のさいころの出た目の数をと$y$として,
右から$y$番目のカードとそれより右にあるすべてのカードを列から取り除きます.
このとき,次の各問いに答えなさい.
${}_{(左)}\boxed{A}\boxed{A}\boxed{A}\boxed{A}\boxed{B}\boxed{B}\boxed{B}\boxed{C}\boxed{C}\boxed{C}\boxed{D}\boxed{D}\boxed{D}_{(右)}$
①取り除かれずに残っているカードが5枚のとき,
$y$を$x$の式で表しなさい.
②取り除かれずに残っているカードの種類が,
3種類となる確率を求めなさい.
この動画を見る
下の図は,$\boxed{A},\boxed{B},\boxed{C},\boxed{D}$の4種類のカードを,
1列に並べたものです. 大小2つのさいころを同時に1回投げます.
大きい方のさいころの出た目の数を入として,
左から$x$番目のカードとそれより左にあるすべてのカードを列から取り除きます.
また,小さい方のさいころの出た目の数をと$y$として,
右から$y$番目のカードとそれより右にあるすべてのカードを列から取り除きます.
このとき,次の各問いに答えなさい.
${}_{(左)}\boxed{A}\boxed{A}\boxed{A}\boxed{A}\boxed{B}\boxed{B}\boxed{B}\boxed{C}\boxed{C}\boxed{C}\boxed{D}\boxed{D}\boxed{D}_{(右)}$
①取り除かれずに残っているカードが5枚のとき,
$y$を$x$の式で表しなさい.
②取り除かれずに残っているカードの種類が,
3種類となる確率を求めなさい.
【高校受験対策】数学-規則性5

単元:
#数学(中学生)#中2数学#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
ます目が書いてあるボード上で,次の規則にしたがって,円形のコマを進める.
<規則>
①最初に,図1のようにボードの左下のます目にコマをおく.
②さいころを1回振って出た目の数が奇数ならば上方向に,
偶数ならば右方向に出た目の数だけコマを進める.
ただし,コマがます目の端まで進めば,それまでとは反対方向にコマを進める.
③続けて2回目のさいころを振るとき,
コマが1回目に進んだ位置から②の規則にしたがってコマを進め,
コマが2回目に進んだ位置をコマが止まるます目とする.
(1)さいころを2回振って,$5→6$の順に目が出た.
$4\times 4$のます目の中で,コマが止まるます目に○印を記入しなさい.
(2)さいころを2回振って,$4\times 4$のます目のボード上でコマを進めたとき,
コマが止まるます目は全部で何個あるか求めなさい.
(3) さいころを2回振って,$5\times 5$のます目(図2)のボード上で,
規則にしたがってコマを進めたとき,
コマが止まるます目は全部で何個あるか求めなさい.
図は動画内参照
この動画を見る
ます目が書いてあるボード上で,次の規則にしたがって,円形のコマを進める.
<規則>
①最初に,図1のようにボードの左下のます目にコマをおく.
②さいころを1回振って出た目の数が奇数ならば上方向に,
偶数ならば右方向に出た目の数だけコマを進める.
ただし,コマがます目の端まで進めば,それまでとは反対方向にコマを進める.
③続けて2回目のさいころを振るとき,
コマが1回目に進んだ位置から②の規則にしたがってコマを進め,
コマが2回目に進んだ位置をコマが止まるます目とする.
(1)さいころを2回振って,$5→6$の順に目が出た.
$4\times 4$のます目の中で,コマが止まるます目に○印を記入しなさい.
(2)さいころを2回振って,$4\times 4$のます目のボード上でコマを進めたとき,
コマが止まるます目は全部で何個あるか求めなさい.
(3) さいころを2回振って,$5\times 5$のます目(図2)のボード上で,
規則にしたがってコマを進めたとき,
コマが止まるます目は全部で何個あるか求めなさい.
図は動画内参照
