 中2数学
中2数学
 中2数学
中2数学
連立方程式だけど、2次式 四天王寺

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け(x>0 , y<0)
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x^2 + y^2 = 9 \\
2x^2 - 3y^2 = -5
\end{array}
\right.
\end{eqnarray}
$
四天王寺高等学校
この動画を見る
連立方程式を解け(x>0 , y<0)
$
\begin{eqnarray}
\left\{
\begin{array}{l}
3x^2 + y^2 = 9 \\
2x^2 - 3y^2 = -5
\end{array}
\right.
\end{eqnarray}
$
四天王寺高等学校
【中学数学】多項式の加法減法の問題演習~計算ミスしない方法~ 1-3【中2数学】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle
(1)\, (3x+2y)+(x+7y)
$
$\displaystyle
(2)\, (5a-3b)+(-a+6b)
$
$\displaystyle
(3)\, (3x^2+y)+(7x^2+3)
$
$\displaystyle
(4)\, (4x+y)-(20x+5y)
$
$\displaystyle
(5)\, (s+3t)-(-s+2t)
$
$\displaystyle
(6)\, (r+x^2)-(x^2-4r)
$
$\displaystyle
(7)\, (6a-3b)-(6a-2b)
$
$\displaystyle
(8)\, (x^2-x-3)-(6x^2+3x-1)
$
$\displaystyle
(9)\, (6x-6y-3)+(5x-4y-8)
$
$\displaystyle
(10)\, (11a-7b-c)-(a-4b+c)
$
この動画を見る
$\displaystyle
(1)\, (3x+2y)+(x+7y)
$
$\displaystyle
(2)\, (5a-3b)+(-a+6b)
$
$\displaystyle
(3)\, (3x^2+y)+(7x^2+3)
$
$\displaystyle
(4)\, (4x+y)-(20x+5y)
$
$\displaystyle
(5)\, (s+3t)-(-s+2t)
$
$\displaystyle
(6)\, (r+x^2)-(x^2-4r)
$
$\displaystyle
(7)\, (6a-3b)-(6a-2b)
$
$\displaystyle
(8)\, (x^2-x-3)-(6x^2+3x-1)
$
$\displaystyle
(9)\, (6x-6y-3)+(5x-4y-8)
$
$\displaystyle
(10)\, (11a-7b-c)-(a-4b+c)
$
連立方程式の代入法について

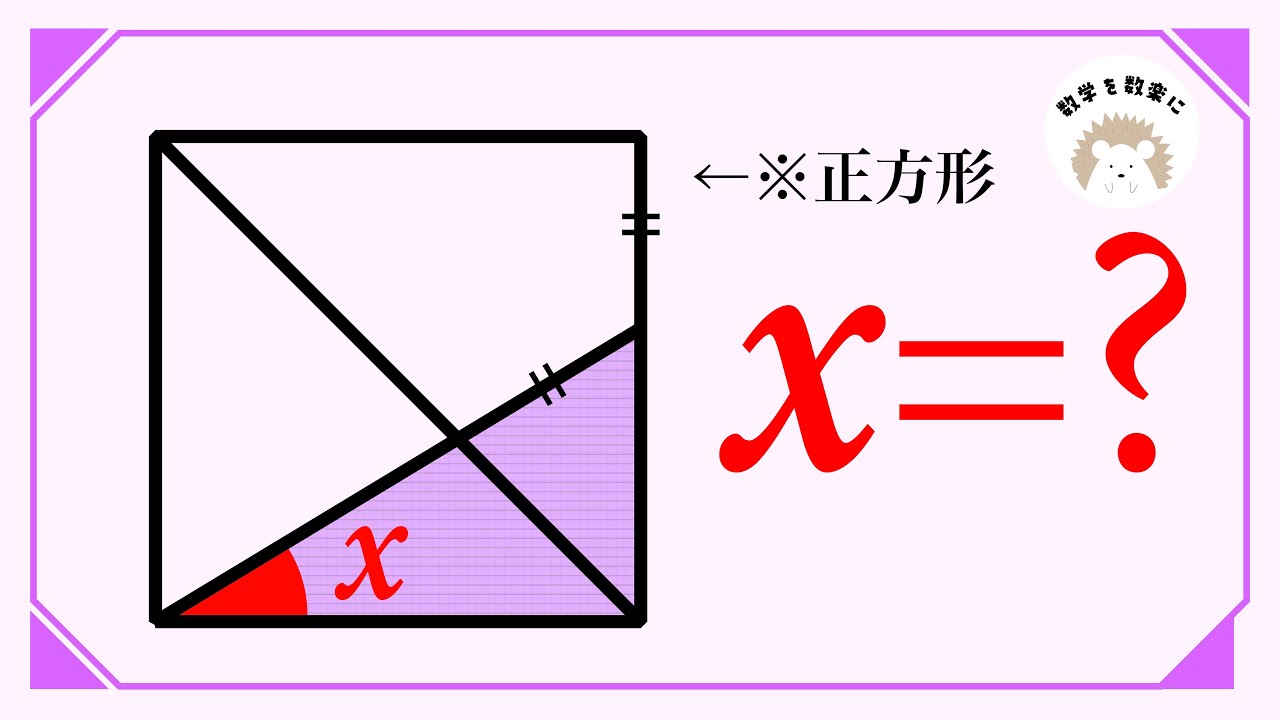
正方形と角
ビッグマックのチーズの値段ってなんぼ?

ビッグマックに連立方程式当てはめてみた

気付けば10秒 知っていれば3秒
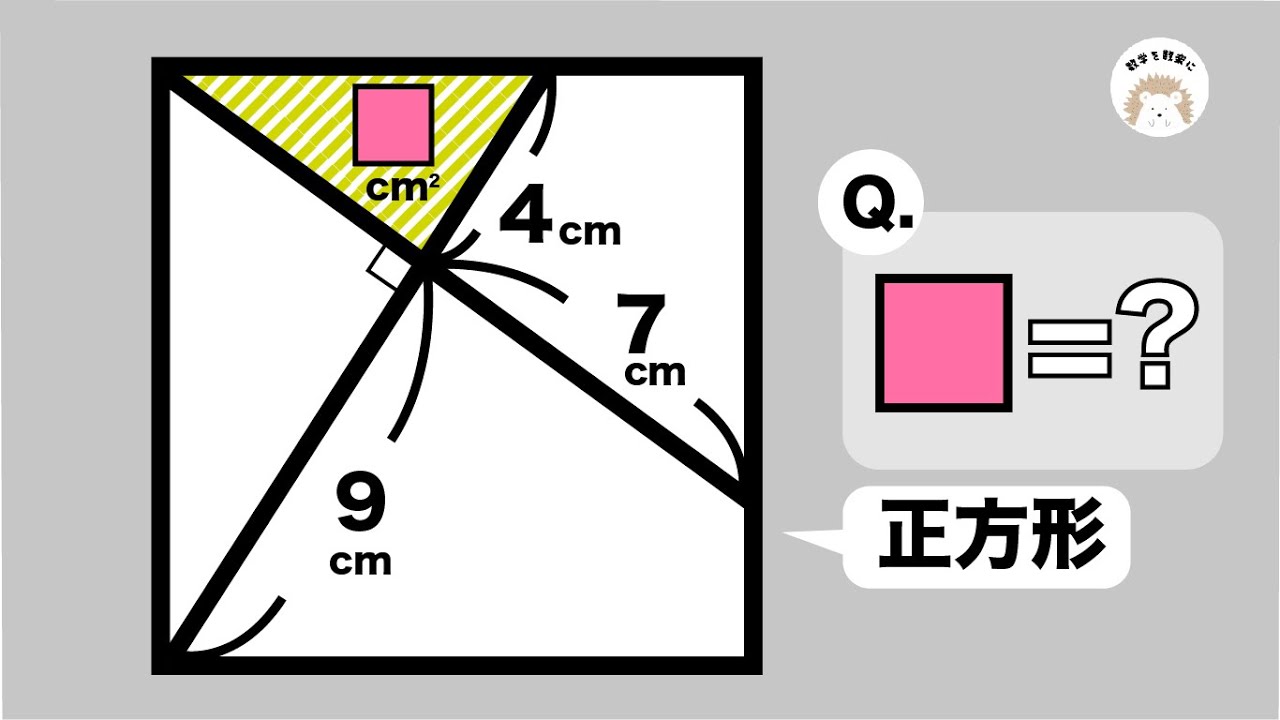
話題の三角関数で加法定理を回転変換して解く~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角関数で加法定理を回転変換して解く解き方に関して解説していきます.
この動画を見る
三角関数で加法定理を回転変換して解く解き方に関して解説していきます.
【数学検定】数学検定3級対策問題1

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#数学検定・数学甲子園・数学オリンピック等#文字と式#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
この動画を見る
数学検定3級対策問題1の解説動画です。
問題1.次の計算をしなさい。
(1) 9-(-5)+(-8)
(2) 24-16÷(-4)
(3) 2³+(-3)²
(4) 35/36 ÷ (-2/9) × 4/7
(5) √125-√45+√20
(6) (√3+4)²-24/√3
(7) 3(3x+5)+4(2x-7)
(8) 0.5(6x-1)-0.8(3x-4)
(9) 7(4x-5y)-2(9x+y)
(10) 3x-6y/8 - 2x-7y/12
(11) -5x²y × 9x²y²
(12) 13x³y²/5 ÷ (-4x²y/5) × (-2xy²/13)
中学生の解き方 小学生の解き方 ベリースライム
単元:
#算数(中学受験)#数学(中学生)#中2数学#過去問解説(学校別)#平面図形#角度と面積#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
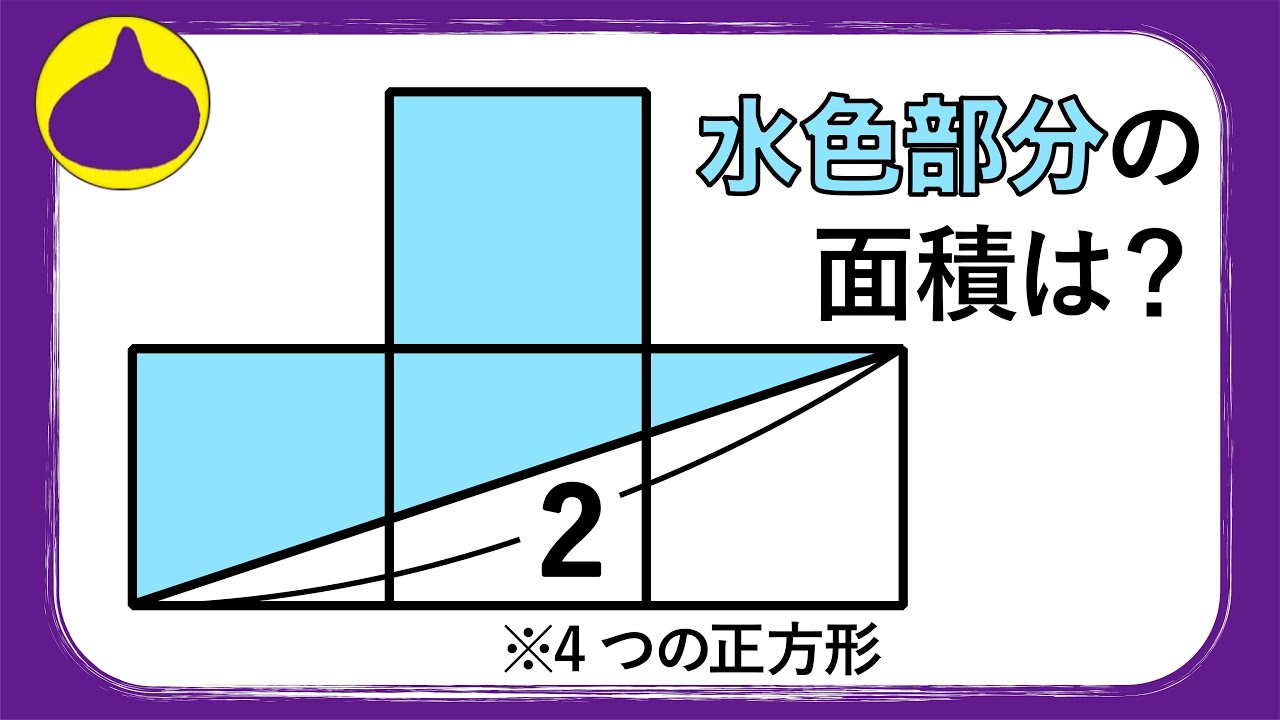
4つの正方形
水色部分の面積は?
*図は動画内参照
この動画を見る
4つの正方形
水色部分の面積は?
*図は動画内参照
【基礎力は身に付いているのか】計算:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
この動画を見る
次の式を計算せよ.
$\left(\dfrac{1}{3}-\dfrac{1}{2}\right)\div \left(-\dfrac{2^2}{5}+\dfrac{1}{2}\right)$
和洋国府台女子高等学校過去問
連立2元4次方程式
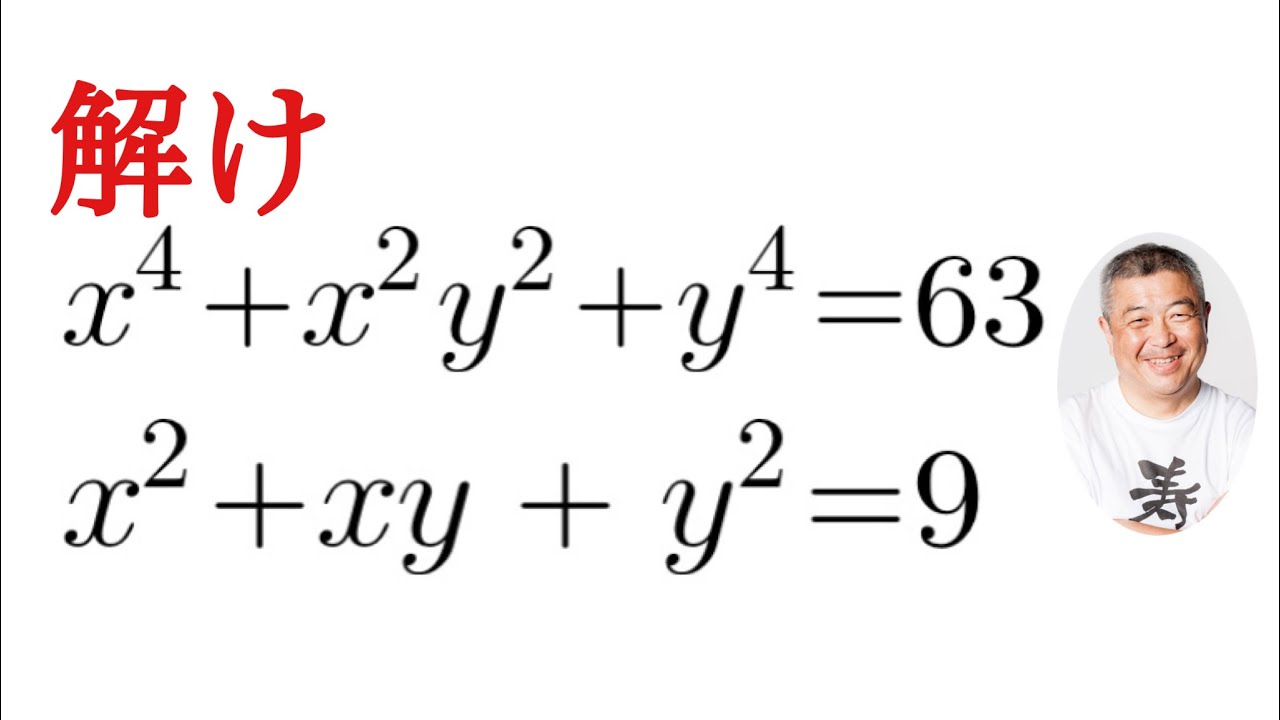
単元:
#連立方程式#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4+x^2y^2+y^4=63 \\
x^2+xy+y^2=9
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^4+x^2y^2+y^4=63 \\
x^2+xy+y^2=9
\end{array}
\right.
\end{eqnarray}$
これを解け.
【3分で好きになる!】連立方程式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
この動画を見る
入試問題 近畿大学附属高等学校
aの値を求めよ。
【連立方程式】
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + y = 5a-13 \\
3x - 2y = -2a+1
\end{array}
\right.
\end{eqnarray}$
の解は、$y$が$x$の$2$倍になっている。
中2数学「1次関数の式」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式
例1 yがxの1次関数であるものをすべて選びなさい。
例2次のxとyの関係について、yをxの式で表しなさい。また、yが1次関数であるものをすべて選びなさい。
(1)120円のりんごを火個買ったときの代金y円
(2) 10kmを歩くとき、歩いた道のりXkmと残りの道のりykm
(3)面積が48cmの長方形の縦Xcm、横ycm
この動画を見る
中2~1次関数の式
例1 yがxの1次関数であるものをすべて選びなさい。
例2次のxとyの関係について、yをxの式で表しなさい。また、yが1次関数であるものをすべて選びなさい。
(1)120円のりんごを火個買ったときの代金y円
(2) 10kmを歩くとき、歩いた道のりXkmと残りの道のりykm
(3)面積が48cmの長方形の縦Xcm、横ycm
中2数学「連立方程式の文章題⑨(食塩水の濃度)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑨~
例13%の食塩水と8%の食塩水を混ぜて、6%の食塩水を (食塩水の濃度) 400g つくります。
3%と8%の食塩水は、それぞれ何g混ぜればよいですか。
この動画を見る
中2~連立方程式の文章題⑨~
例13%の食塩水と8%の食塩水を混ぜて、6%の食塩水を (食塩水の濃度) 400g つくります。
3%と8%の食塩水は、それぞれ何g混ぜればよいですか。
【方針が立っても完答は…!】連立方程式:東京学芸大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
この動画を見る
$x,y$についての連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
2ax-7y=236 \\
x+2y=\dfrac{a}{7}
\end{array}
\right.
\end{eqnarray}$
の解が$x=3,y=b$である.
このとき,定数$a,b$の値を求めなさい.
東京学芸大高校過去問
数学を数楽にして解く

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$26 \times 78 \times (-5)^2$
広島大学附属高等学校
この動画を見る
$26 \times 78 \times (-5)^2$
広島大学附属高等学校
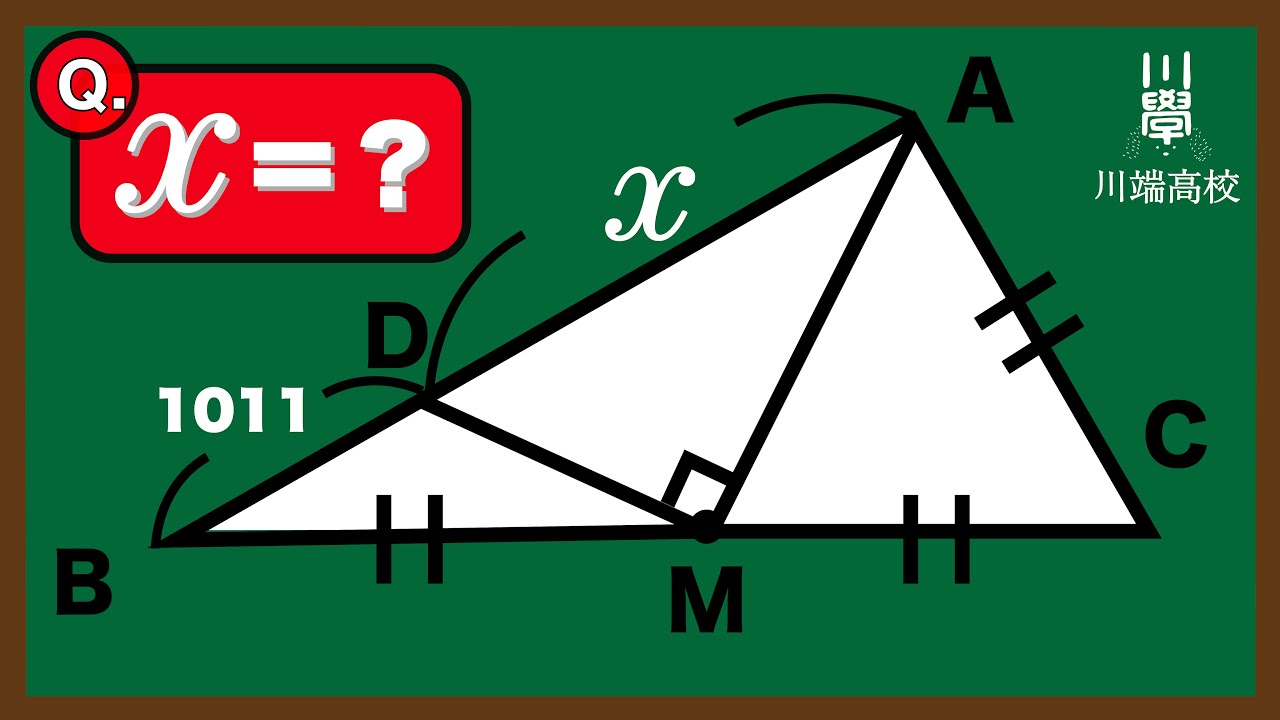
補助線どう引く?
中2数学「連立方程式の文章題⑧(割合の増減)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑧~
例題
ある中学校の昨年の生徒数は500人でしたが、
今年は、昨年に比べて男子が6%増加し 女子が8%減少したので、全体で12人減りました。
今年の男子と女子の生徒数を求めなさい。
この動画を見る
中2~連立方程式の文章題⑧~
例題
ある中学校の昨年の生徒数は500人でしたが、
今年は、昨年に比べて男子が6%増加し 女子が8%減少したので、全体で12人減りました。
今年の男子と女子の生徒数を求めなさい。
中2数学「連立方程式の文章題⑦(電車の速さ)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑦~
例題
ある電車が1.5kmの鉄橋を渡り始めてから渡り終わる (電車の速さ) までに、1分10秒かかりました。
また、同じ早さで1.2kmのトンネルを通過するとき、電車が完全にかくれていたのは38秒でした。
この電車の長さは何mですか。また、速さは秒速何mですか。
この動画を見る
中2~連立方程式の文章題⑦~
例題
ある電車が1.5kmの鉄橋を渡り始めてから渡り終わる (電車の速さ) までに、1分10秒かかりました。
また、同じ早さで1.2kmのトンネルを通過するとき、電車が完全にかくれていたのは38秒でした。
この電車の長さは何mですか。また、速さは秒速何mですか。
連立3元4次方程式
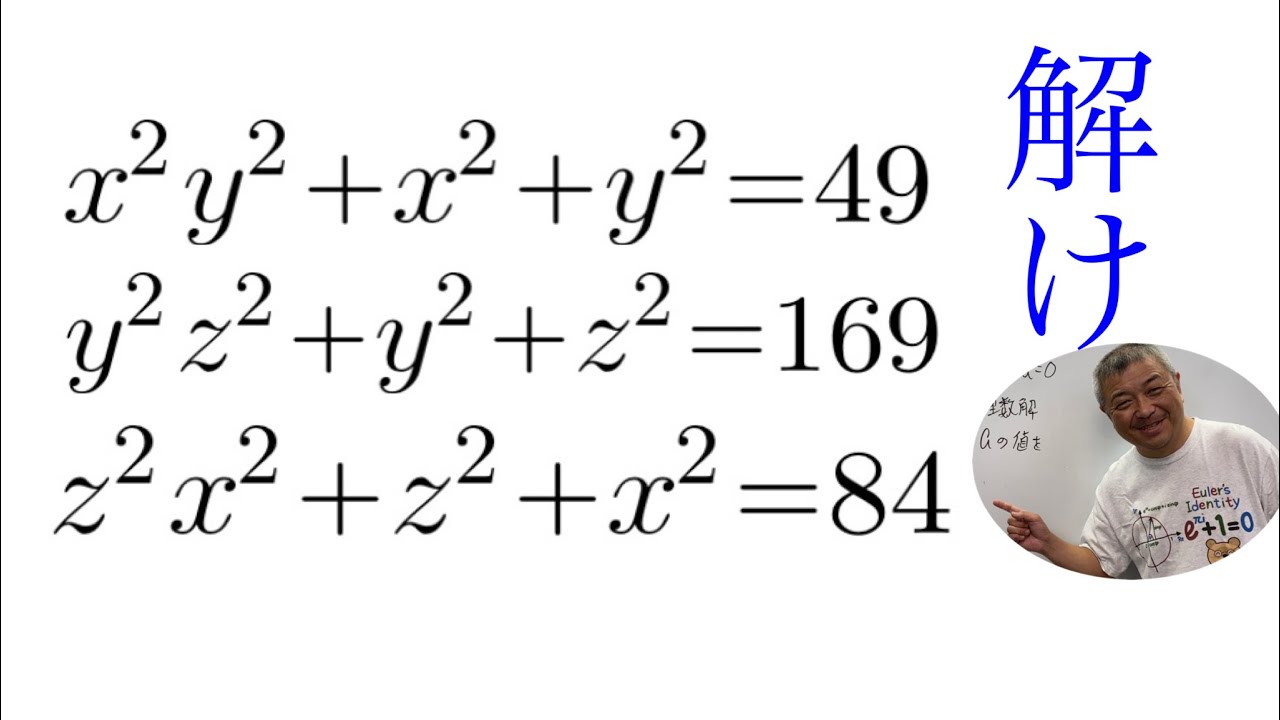
単元:
#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y^2+x^2+y^2=49 \\
y^2z^2+y^2+z^2=169\\
z^2x^2+z^2+x^2=84 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y^2+x^2+y^2=49 \\
y^2z^2+y^2+z^2=169\\
z^2x^2+z^2+x^2=84 \\
\end{array}
\right.
\end{eqnarray}$
これを解け.
中2数学「連立方程式の文章題⑥(池の周りの速さ)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑥~ (池の周りの速さ)
例題
1周2kmの池の周りを兄と弟が同じ位置から同時に 出発します。
反対方向に進むと、出発してから5分後に 2人は、初めて出会います。
また、 同じ方向に進むと 出発してから20分後に兄は、弟を追いこします。兄と弟の速さは、それぞれ分速何mですか。
この動画を見る
中2~連立方程式の文章題⑥~ (池の周りの速さ)
例題
1周2kmの池の周りを兄と弟が同じ位置から同時に 出発します。
反対方向に進むと、出発してから5分後に 2人は、初めて出会います。
また、 同じ方向に進むと 出発してから20分後に兄は、弟を追いこします。兄と弟の速さは、それぞれ分速何mですか。
【簡潔に予習・復習!】多項式(式の利用):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
中2数学「連立方程式の文章題⑤(速さが変わる問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題⑤~
例題
家から1.2km離れた駅まで行くのに、はじめは分速50mで歩き、途中から分速100mで走ったら、家を出てから19分後に駅に着きました。
歩いた道のり、走った道のりはそれぞれ何mですか。
この動画を見る
中2~連立方程式の文章題⑤~
例題
家から1.2km離れた駅まで行くのに、はじめは分速50mで歩き、途中から分速100mで走ったら、家を出てから19分後に駅に着きました。
歩いた道のり、走った道のりはそれぞれ何mですか。
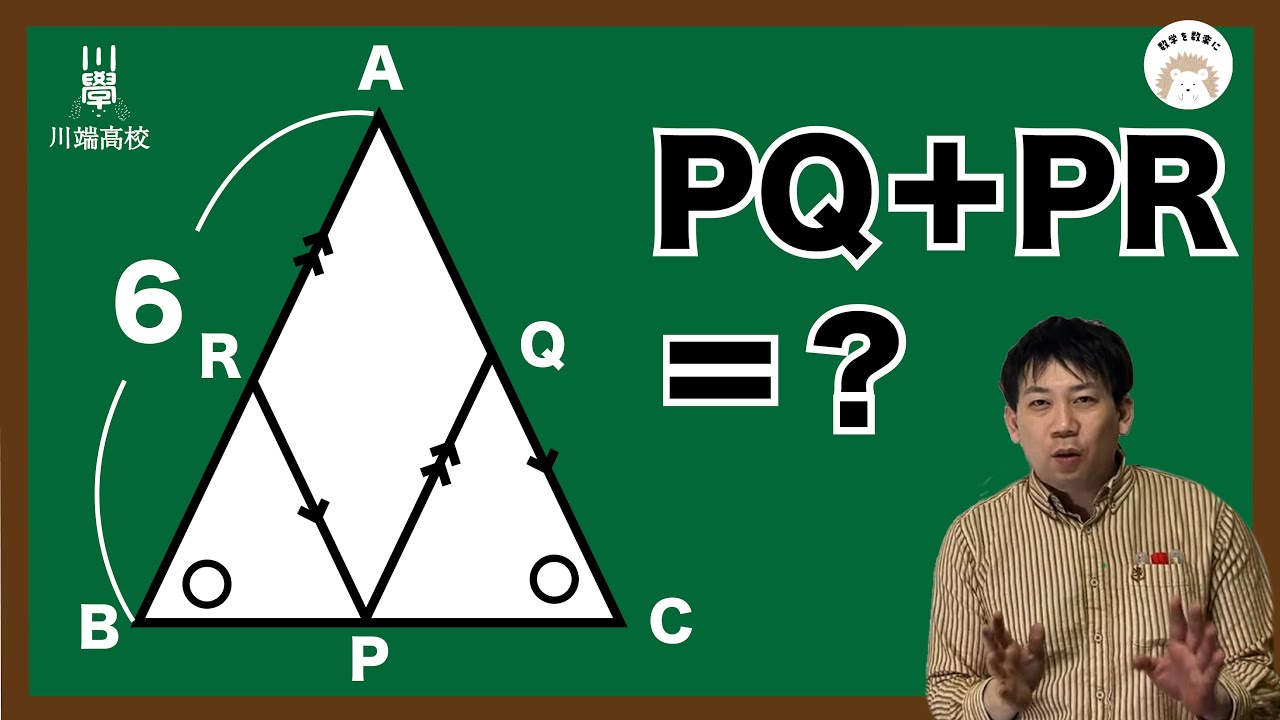
気付けば一瞬!!
【簡潔に予習・復習!】多項式(後編):式の展開と因数分解~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
【簡潔に予習・復習!】多項式(前編):教科書順で内容確認~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
多項式に関して解説していきます.
この動画を見る
多項式に関して解説していきます.
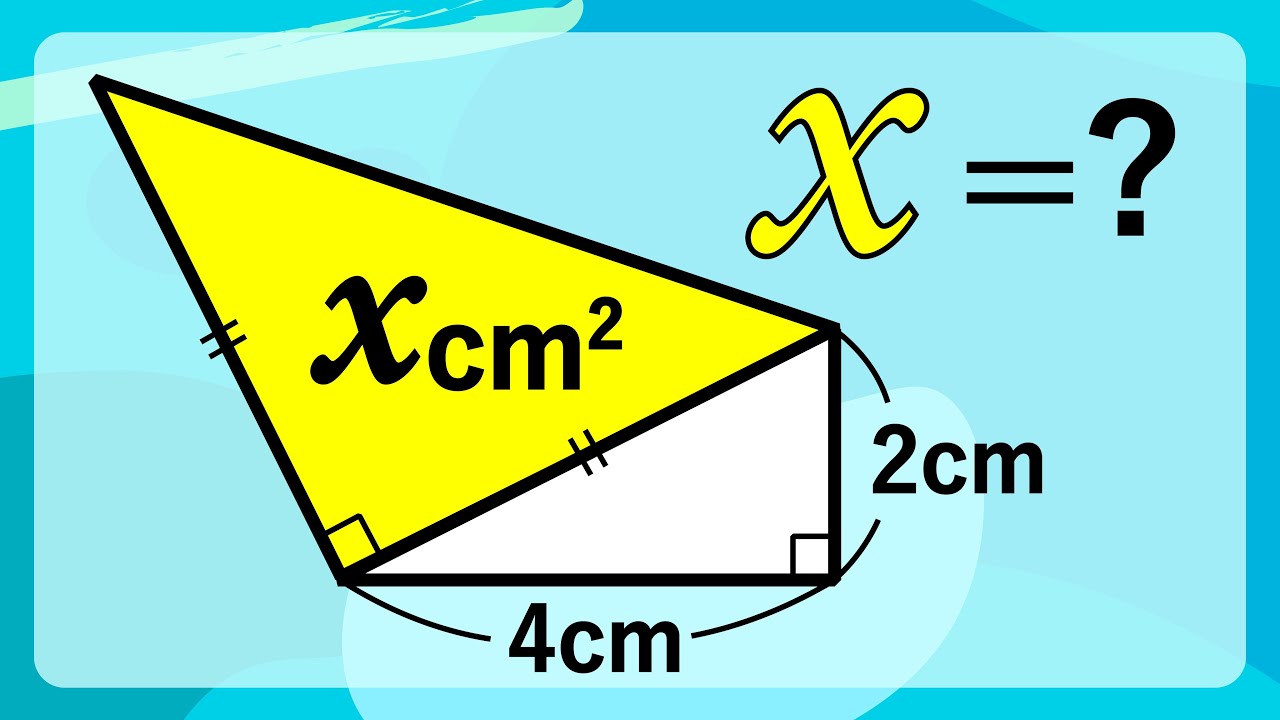
三平方の定理を使わずに解くこともできます
中2数学「連立方程式の文章題④(度数分布表の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題④~
例題
次の表は、あるクラス40人の通学時間を度数分布表で 整理したものです。
この表から求めた平均値がちょうど20分のとき、x、yの値を求めよ。
この動画を見る
中2~連立方程式の文章題④~
例題
次の表は、あるクラス40人の通学時間を度数分布表で 整理したものです。
この表から求めた平均値がちょうど20分のとき、x、yの値を求めよ。
正負の数の計算、工夫しよう!膳所高校

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$42.9 \times \frac{5}{13} - 14.3 \times (\frac{7}{26} - \frac{1}{13} + \frac{1}{2})$
膳所高等学校
この動画を見る
$42.9 \times \frac{5}{13} - 14.3 \times (\frac{7}{26} - \frac{1}{13} + \frac{1}{2})$
膳所高等学校
