 中2数学
中2数学
 中2数学
中2数学
1=5として,これ解けますか?

単元:
#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1=5として
2=25
3=325
4=4325
5=?
この動画を見る
1=5として
2=25
3=325
4=4325
5=?
中2数学「連立方程式の文章題③(平均の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題③~(平均の問題)
例題
中学生80人が数学のテストを受けたら、全体の平均が58点。男子の平均が52点,女子の平均が62点でした。
男子と女子の人数を求めなさい。
この動画を見る
中2~連立方程式の文章題③~(平均の問題)
例題
中学生80人が数学のテストを受けたら、全体の平均が58点。男子の平均が52点,女子の平均が62点でした。
男子と女子の人数を求めなさい。
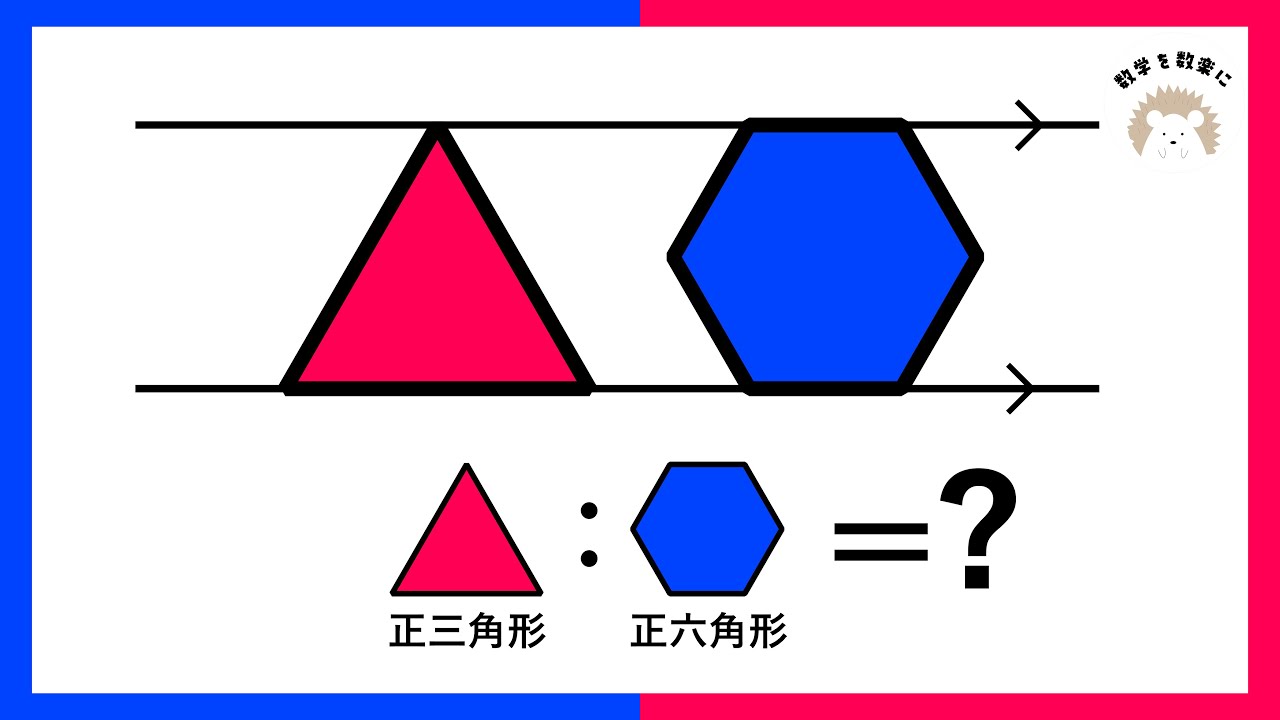
気付けば一瞬!!正三角形と正六角形の面積比
中2数学「連立方程式の文章題②(2けたの整数問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題②~ (2けたの整数問題)
例題
2けたの正の整数があり、十の位の数と一の位の数の和は11です。 また、十の位と一の位を入れかえてできる2けたの整数は、 もとの数より45小さくなります。
もとの2けたの整数を求めなさい。
この動画を見る
中2~連立方程式の文章題②~ (2けたの整数問題)
例題
2けたの正の整数があり、十の位の数と一の位の数の和は11です。 また、十の位と一の位を入れかえてできる2けたの整数は、 もとの数より45小さくなります。
もとの2けたの整数を求めなさい。
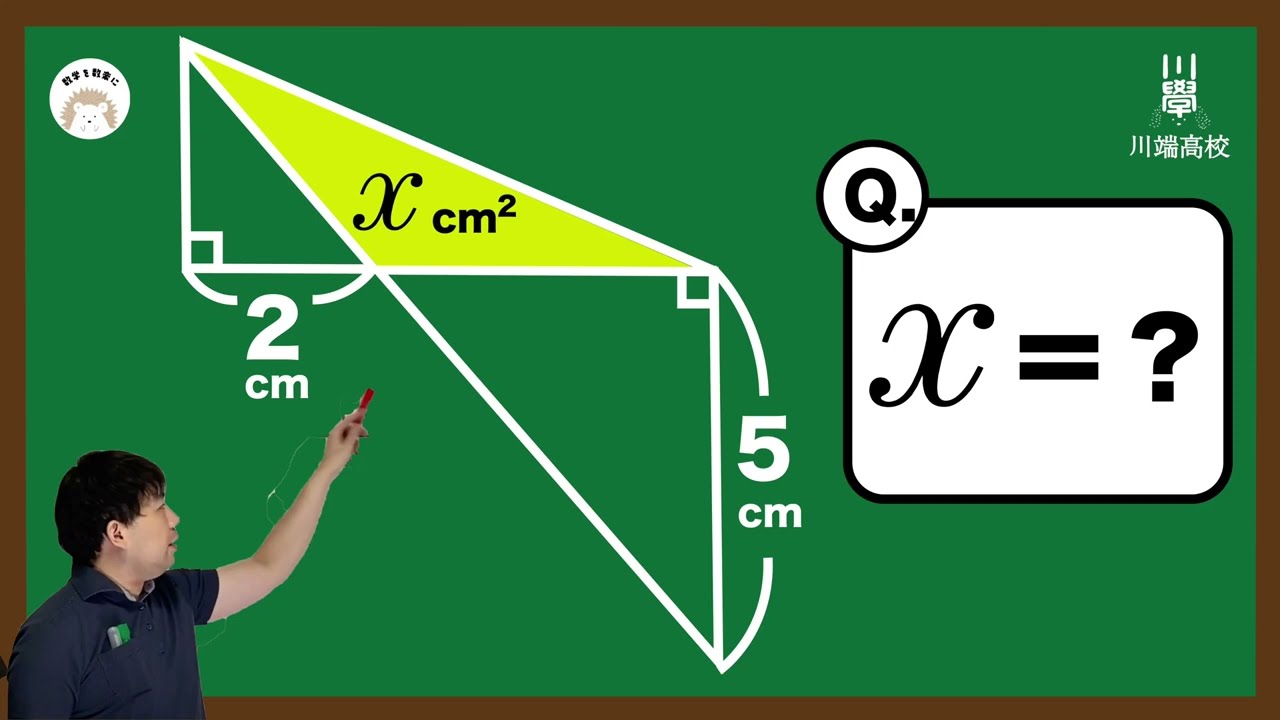
これ解ける?
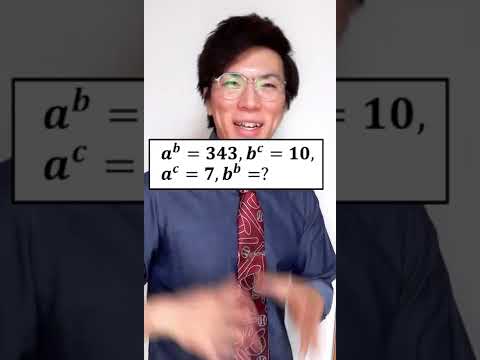
中2数学「連立方程式の文章題①(代金の問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式の文章題①~
例題
1枚60円の色紙Aと1枚80円の色紙Bを合わせて20枚買ったら、 代金の合計は1440円でした。
色紙Aと 紙Bはそれ ぞれ何枚買いましたか。
この動画を見る
中2~連立方程式の文章題①~
例題
1枚60円の色紙Aと1枚80円の色紙Bを合わせて20枚買ったら、 代金の合計は1440円でした。
色紙Aと 紙Bはそれ ぞれ何枚買いましたか。
気付けば一瞬!!積の値どう考える?
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
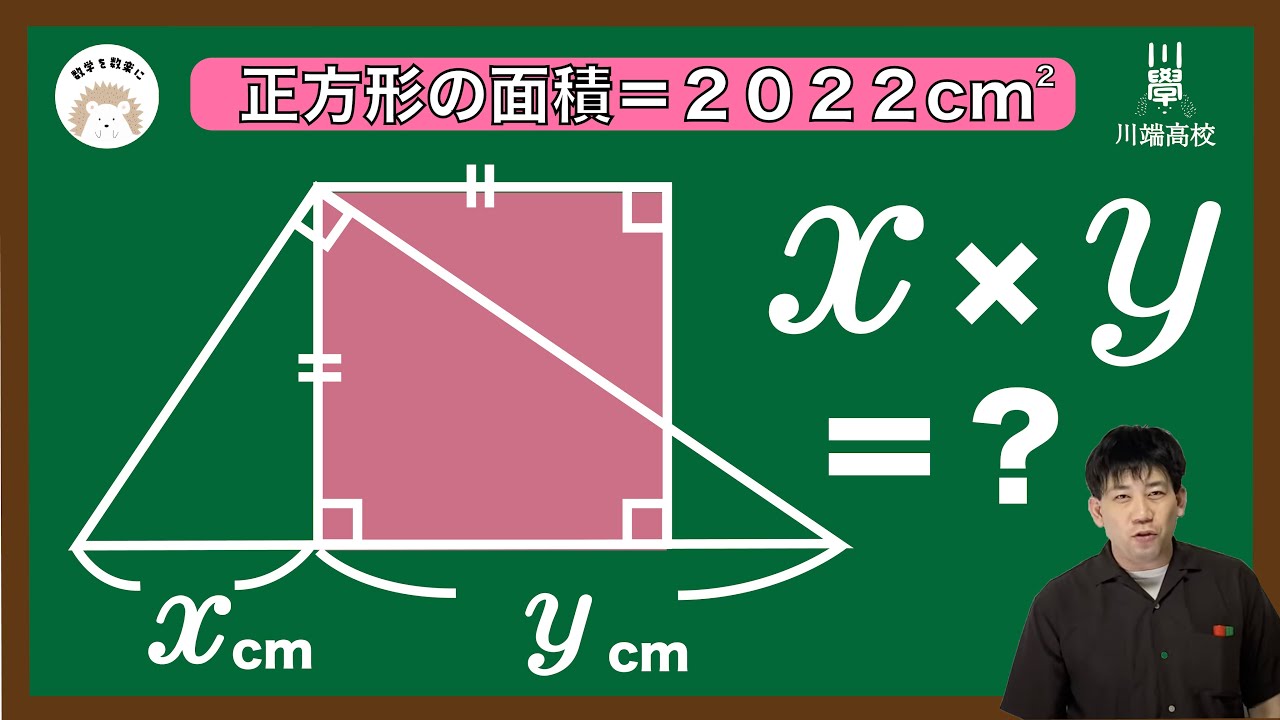
正方形の面積=2022㎠
$x \timse y =?$
*図は動画内参照
川端高校
この動画を見る
正方形の面積=2022㎠
$x \timse y =?$
*図は動画内参照
川端高校
【何を問われているか理解しているか?】計算:鎌倉学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
この動画を見る
次の計算をしなさい.
${{2^3-(-2)^3}}\times{-2^5+(-2)^5}$
鎌倉学園高校過去問
気づけば一瞬!!!
動体視力と数学を鍛えるサウンド~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
この動画を見る
次の$\Box$をうめなさい.
$624^2-623\times625=\Box$
土浦日大高校過去問
中2数学「解を利用する連立方程式の問題」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~解を利用する連立方程式の問題~
例題
例1 $\begin{eqnarray}
\left\{
\begin{array}{l}
ax-by=4 \\
bx-ay~=5
\end{array}
\right.
\end{eqnarray}$
の解が$x=2.y=-1$のとき、$a,b$の値を求めなさい。
例2 次の2つの連立方程式が同じ解をもつとき、a.bの値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=3 \\
2ax-by=-11
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=-1 \\
x+y=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~解を利用する連立方程式の問題~
例題
例1 $\begin{eqnarray}
\left\{
\begin{array}{l}
ax-by=4 \\
bx-ay~=5
\end{array}
\right.
\end{eqnarray}$
の解が$x=2.y=-1$のとき、$a,b$の値を求めなさい。
例2 次の2つの連立方程式が同じ解をもつとき、a.bの値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+y=3 \\
2ax-by=-11
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax+by=-1 \\
x+y=-1
\end{array}
\right.
\end{eqnarray}$
中2数学「分母にx,yがある連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~分母に父とがある連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{x}+\dfrac{2}{y}=17 \\
\dfrac{5}{x}-\dfrac{3}{y}=3
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x}-1+y=-1 \\
\dfrac{2}{x}-1+\dfrac{y}{2}=4
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~分母に父とがある連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{x}+\dfrac{2}{y}=17 \\
\dfrac{5}{x}-\dfrac{3}{y}=3
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{1}{x}-1+y=-1 \\
\dfrac{2}{x}-1+\dfrac{y}{2}=4
\end{array}
\right.
\end{eqnarray}$
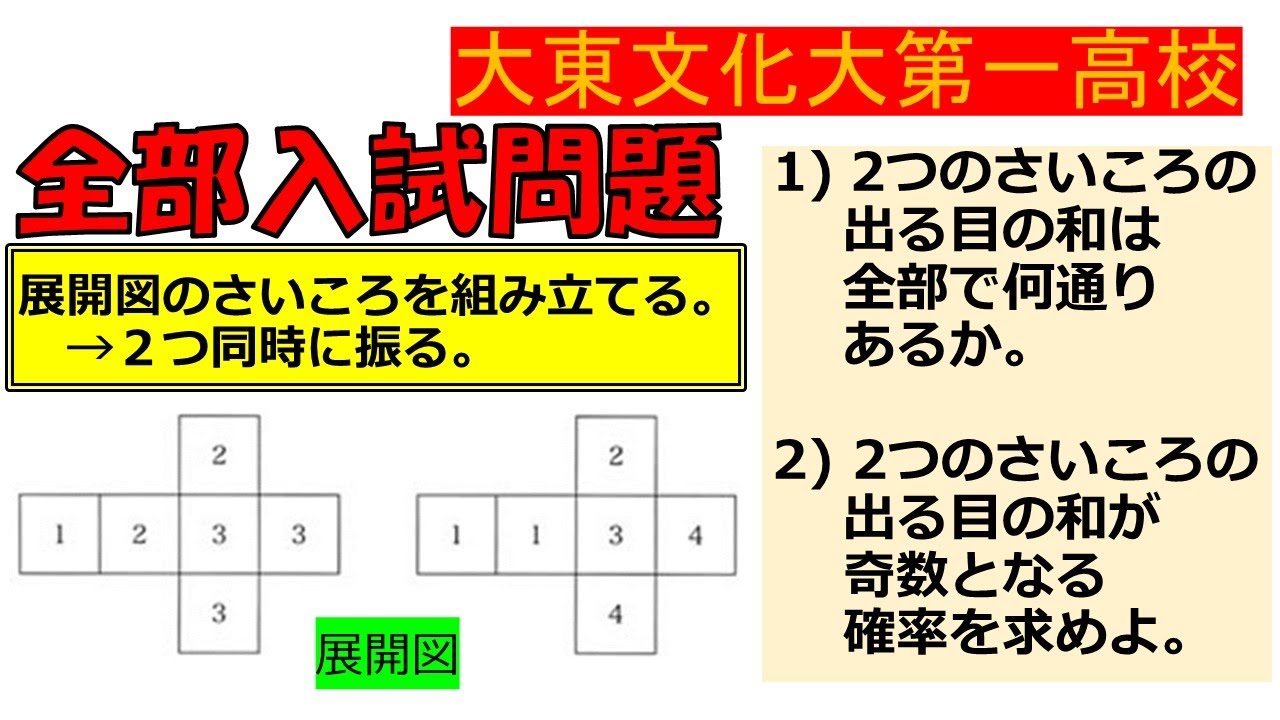
【1分で方向性を理解!】確率:大東文化大学第一高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
展開図のさいころを組み立て,2つ同時に振る.
(1)2つのさいころの出る目の和は全部で何通りあるか.
(2)2つのさいころの出る目の和が奇数となる確率を求めよ.
大東文化大第一高校過去問
この動画を見る
展開図のさいころを組み立て,2つ同時に振る.
(1)2つのさいころの出る目の和は全部で何通りあるか.
(2)2つのさいころの出る目の和が奇数となる確率を求めよ.
大東文化大第一高校過去問
中2数学「x,y,zの連立方程式(連立3元1次方程式)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中 2-X、Y、その連立方程式~
例題
次の連立方程式を解きなさい。
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
y+z=2 \\
z+x=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y-2z=11 \\
2x+3y+z=-6 \\
5x-2y+3z=13
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中 2-X、Y、その連立方程式~
例題
次の連立方程式を解きなさい。
(1)$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=3 \\
y+z=2 \\
z+x=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-y-2z=11 \\
2x+3y+z=-6 \\
5x-2y+3z=13
\end{array}
\right.
\end{eqnarray}$
【6分でマスター!!】単項式と多項式の次数の求め方を解説!(係数と定数項についても)〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
単項式と多項式の次数の求め方について解説します。
この動画を見る
数学1A
単項式と多項式の次数の求め方について解説します。
【中学数学】式の値~問題演習で解き方を教えます~ 1-2【中2数学】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $a=5,~b=-8$のとき、$4(2a-7b)-5(a-5b)$を求めよ
(2) $a=6,~b=-7$のとき、$5a^3b^2\div 15a^2b^4\times 2ab^3$を求めよ
(3) $x=\frac{3}{2},~y=-\frac{2}{17}$のとき、$(8x+3y)-2(3x-7y+1)$を求めよ
この動画を見る
(1) $a=5,~b=-8$のとき、$4(2a-7b)-5(a-5b)$を求めよ
(2) $a=6,~b=-7$のとき、$5a^3b^2\div 15a^2b^4\times 2ab^3$を求めよ
(3) $x=\frac{3}{2},~y=-\frac{2}{17}$のとき、$(8x+3y)-2(3x-7y+1)$を求めよ
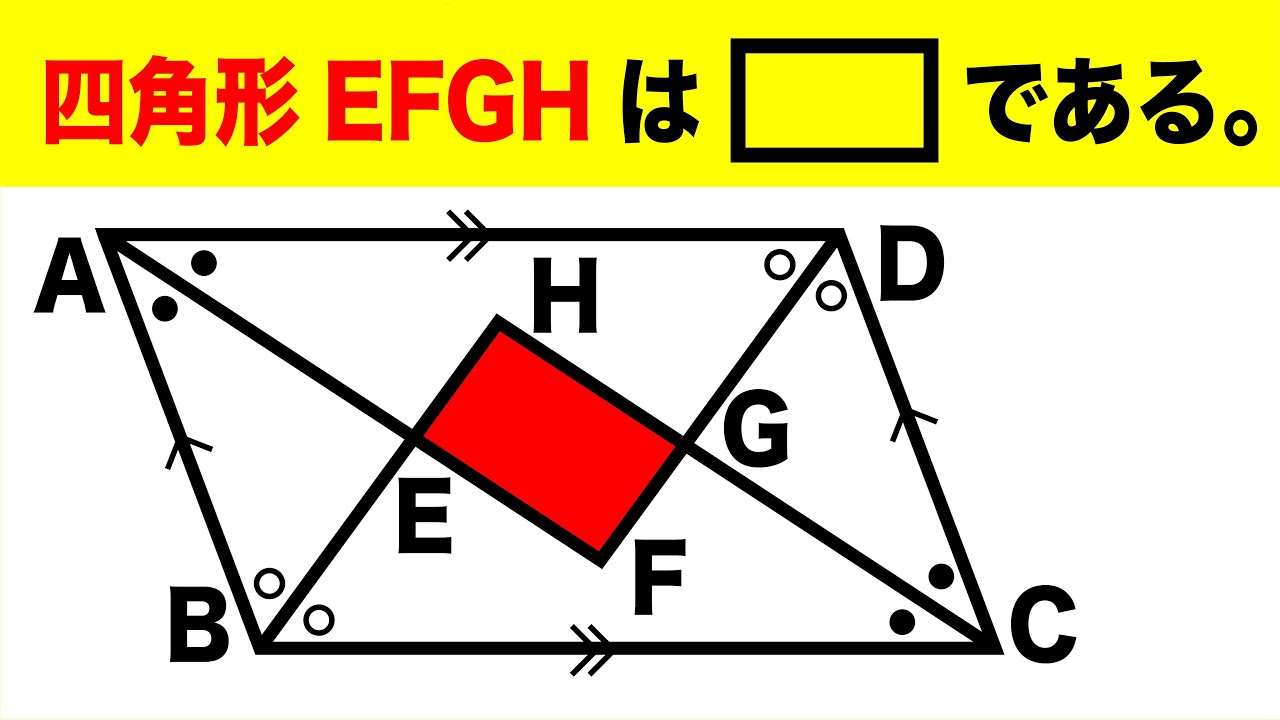
平行四辺形と角の二等分
中2数学「比例式・A=B=Cの連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~比例式・A=B=Cの連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+y=32 \\
x:y=3:4
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+5y=9 \\
(x+5):(y-1)=3:2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~比例式・A=B=Cの連立方程式~
例題
次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+y=32 \\
x:y=3:4
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+5y=9 \\
(x+5):(y-1)=3:2
\end{array}
\right.
\end{eqnarray}$
中2数学「かっこ・分数・小数の連立方程式」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~かっこ・分数・小数の連立方程式~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=1 \\
2x-11=3(x+y)
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-7=-3(y+2) \\
5x+6=2(y-5)
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~かっこ・分数・小数の連立方程式~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=1 \\
2x-11=3(x+y)
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-7=-3(y+2) \\
5x+6=2(y-5)
\end{array}
\right.
\end{eqnarray}$
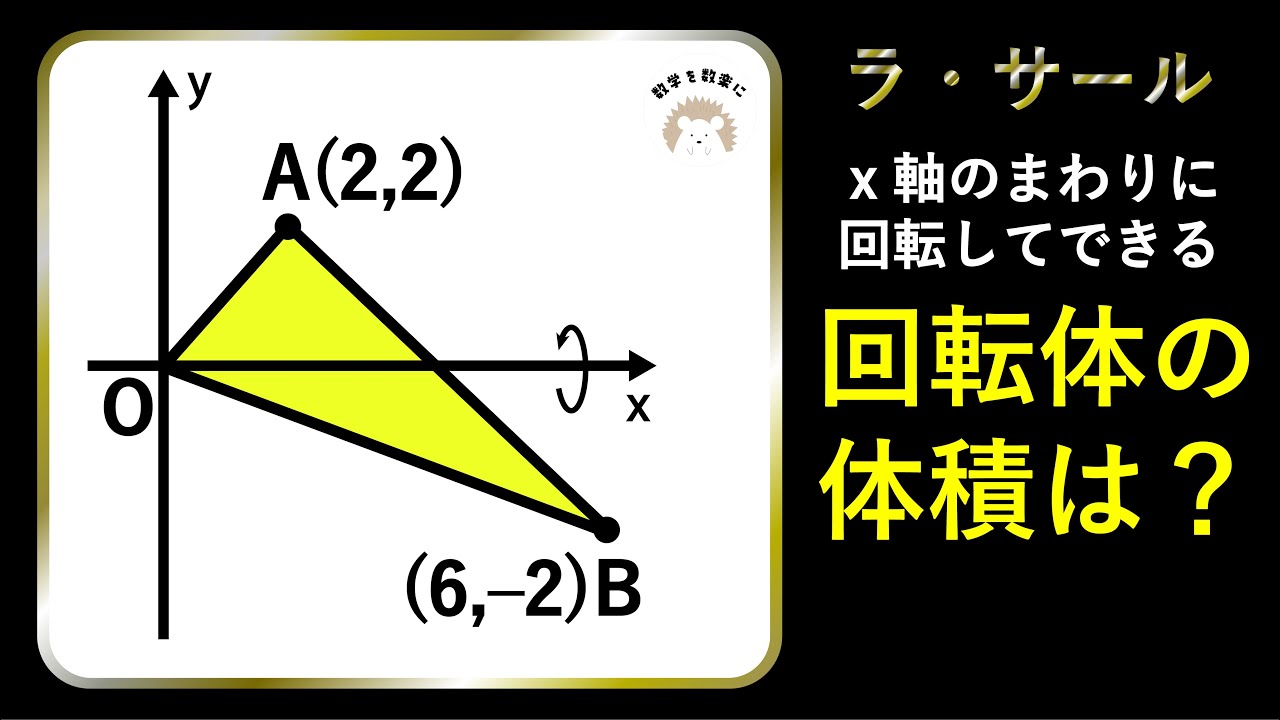
難易度高いよ。回転体 ラ・サール
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
x軸のまわりに回転してできる回転体の体積は?
*図は動画内参照
ラ・サール高等学校
この動画を見る
x軸のまわりに回転してできる回転体の体積は?
*図は動画内参照
ラ・サール高等学校
中2数学「連立方程式(代入法)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式(代入法)~
例題次の連立方程式を解きなさい
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-2y=5 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2y-9 \\
-x+y=6
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
-4x+3y=14 \\
3y=-2x+2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~連立方程式(代入法)~
例題次の連立方程式を解きなさい
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-2y=5 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2y-9 \\
-x+y=6
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
-4x+3y=14 \\
3y=-2x+2
\end{array}
\right.
\end{eqnarray}$
マクドの価格設定大丈夫そ?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
マクドナルドでダブルチーズバーガー1つ買うよりチーズバーガー2つ買う方が
得?数学的に説明動画
この動画を見る
マクドナルドでダブルチーズバーガー1つ買うよりチーズバーガー2つ買う方が
得?数学的に説明動画
中2数学「連立方程式(加減法)」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~連立方程式(加減法)~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=11 \\
2x-3y=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x-5y=7 \\
-2x+3y=-1
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y-16 \\
3x-4y=7
\end{array}
\right.
\end{eqnarray}$
(4)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-6y=-8 \\
9x-4y=6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中2~連立方程式(加減法)~
例題次の連立方程式を解きなさい。
(1)
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x-3y=11 \\
2x-3y=7
\end{array}
\right.
\end{eqnarray}$
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x-5y=7 \\
-2x+3y=-1
\end{array}
\right.
\end{eqnarray}$
(3)
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y-16 \\
3x-4y=7
\end{array}
\right.
\end{eqnarray}$
(4)
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x-6y=-8 \\
9x-4y=6
\end{array}
\right.
\end{eqnarray}$
中2数学「連立方程式と解」【毎日配信】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~第11回連立方程式と解~
例題次のア~ウの中で、連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=8 \\
5x-3y=7
\end{array}
\right.
\end{eqnarray}$
の解はどれか?
ア $x=4,y=-2$
イ $x=5,y=6$
ウ $x=2,y=1$
この動画を見る
中2~第11回連立方程式と解~
例題次のア~ウの中で、連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x+2y=8 \\
5x-3y=7
\end{array}
\right.
\end{eqnarray}$
の解はどれか?
ア $x=4,y=-2$
イ $x=5,y=6$
ウ $x=2,y=1$
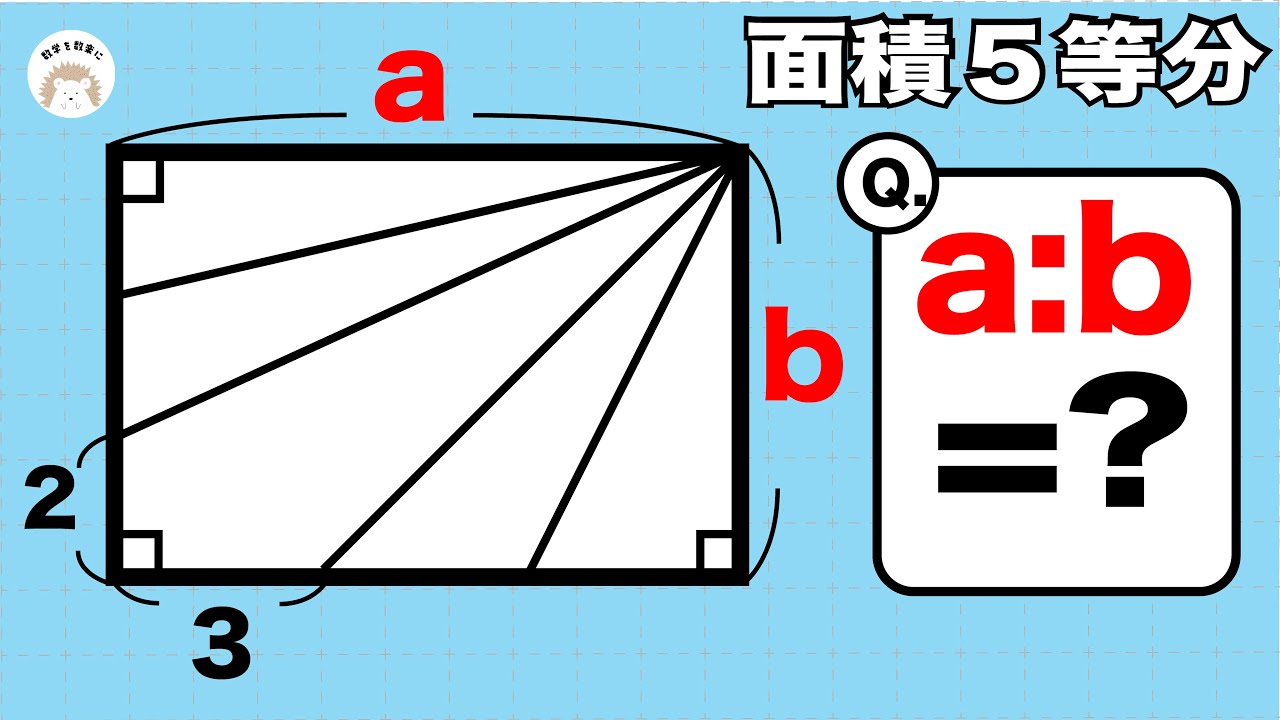
長方形の面積5等分
中2数学「式による説明④(カレンダー問題)」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~第10回式による説明④(カレンダー問題)
(1)枠Aのように、 縦に並んだ3つの数の和は、 真ん中の数の3倍にな ることを説明しなさい。
この動画を見る
中2~第10回式による説明④(カレンダー問題)
(1)枠Aのように、 縦に並んだ3つの数の和は、 真ん中の数の3倍にな ることを説明しなさい。
ポケモンで数学を使おう!

単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ポケモンでマヒ状態かつ混乱のとき攻撃できない確率はどれくらいですか?
この動画を見る
ポケモンでマヒ状態かつ混乱のとき攻撃できない確率はどれくらいですか?
【正面から当たりますか?】確率:早稲田大学系属早稲田佐賀高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$①$~$④$のうち・・・正しいものをすべて選べ.
$①$2人がじゃんけんを1回するとき,勝負が決まる確率は$\dfrac{2}{3}$である.
$②$2枚の硬貨を同時に投げるとき,1枚は表で1枚は裏が出る確率は$\dfrac{1}{3}$である.
$③$当たりが3本,ハズレが7本入っているくじがある.一度引いたくじはもとに戻さないとして,
A君とB君がこの順番でくじを引くとき,A君が当たりを引く確率はB君が当たりを引く確率より
低い.
$④$2個のさいころを同時に投げるとき,同じ目が出る確率は$\dfrac{1}{6}$である.
早稲田佐賀高校過去問
この動画を見る
$①$~$④$のうち・・・正しいものをすべて選べ.
$①$2人がじゃんけんを1回するとき,勝負が決まる確率は$\dfrac{2}{3}$である.
$②$2枚の硬貨を同時に投げるとき,1枚は表で1枚は裏が出る確率は$\dfrac{1}{3}$である.
$③$当たりが3本,ハズレが7本入っているくじがある.一度引いたくじはもとに戻さないとして,
A君とB君がこの順番でくじを引くとき,A君が当たりを引く確率はB君が当たりを引く確率より
低い.
$④$2個のさいころを同時に投げるとき,同じ目が出る確率は$\dfrac{1}{6}$である.
早稲田佐賀高校過去問
【中学数学】多項式の計算~単項式・多項式・次数・定数項・同類項~ 1-1【中2数学】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$
\begin{align}
& 以下の多項式の項を答えろ\\
& (1)\ s + 3t\\
& (2)\ 3x + 4xy\\
\\
&次の式は何次式か\\
& (3)\ 3x^2 + 2x + y^2\\
& (4)\ t^{50} + abc + 7
\end{align}
$
この動画を見る
$
\begin{align}
& 以下の多項式の項を答えろ\\
& (1)\ s + 3t\\
& (2)\ 3x + 4xy\\
\\
&次の式は何次式か\\
& (3)\ 3x^2 + 2x + y^2\\
& (4)\ t^{50} + abc + 7
\end{align}
$
9つの正方形と角の和
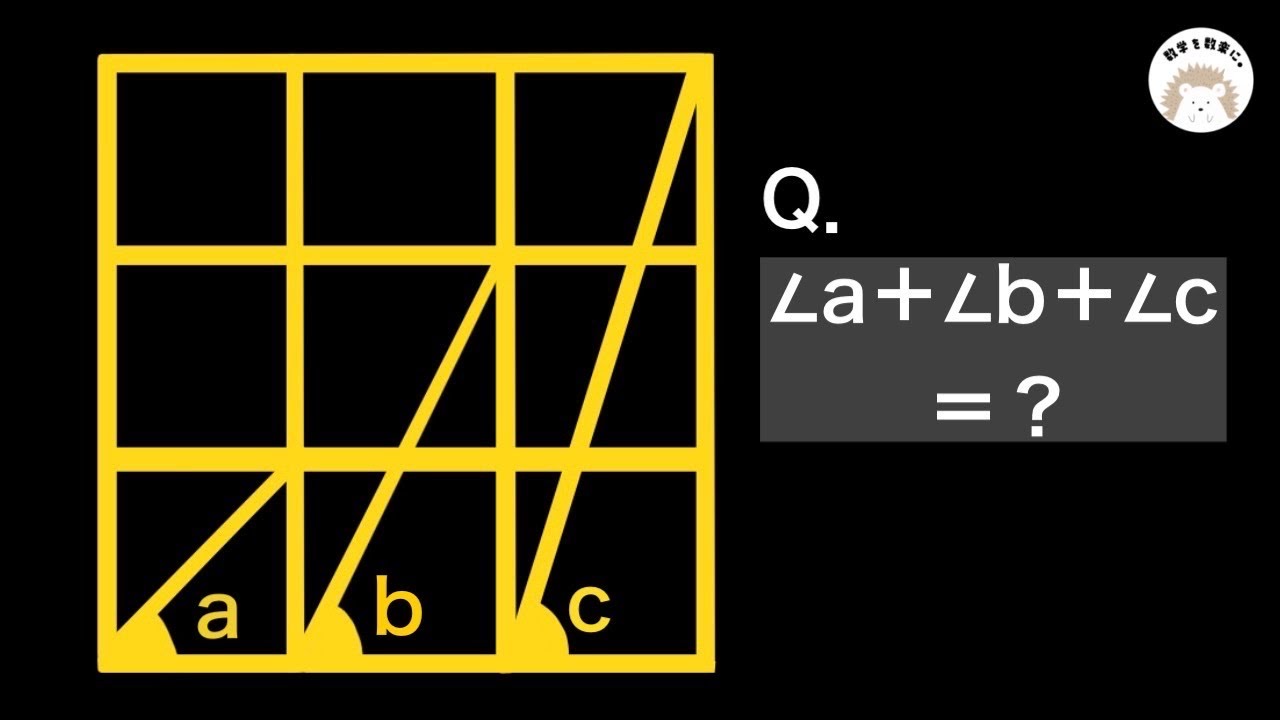
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a + \angle b +\angle c=? $
*図は動画内参照
この動画を見る
$\angle a + \angle b +\angle c=? $
*図は動画内参照
