式の計算(展開、因数分解)
式の計算(展開、因数分解)
 式の計算(展開、因数分解)
式の計算(展開、因数分解)
【中学数学】式の計算の利用の演習~展開の文章題・土地の大きさ~ 1-8.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
縦am、横2amの長方形の土地があります。
この土地の縦を5m長くし、横を3m短くすると、面積はもとの土地よりどれだけ大きくなるか。
また、このとき、面積が55m²大きくなるとすると、もとの土地の縦の長さは何mですか。
この動画を見る
縦am、横2amの長方形の土地があります。
この土地の縦を5m長くし、横を3m短くすると、面積はもとの土地よりどれだけ大きくなるか。
また、このとき、面積が55m²大きくなるとすると、もとの土地の縦の長さは何mですか。
【中学数学】式の計算の利用の演習~展開の文章題~ 1-8.5【中3数学】

単元:
#中3数学#式の計算(展開、因数分解)#三平方の定理
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図の正方形で色のついた部分の面積をa,bを使った式で表せ。
この動画を見る
動画内の図の正方形で色のついた部分の面積をa,bを使った式で表せ。
式の値 昭和学院秀英
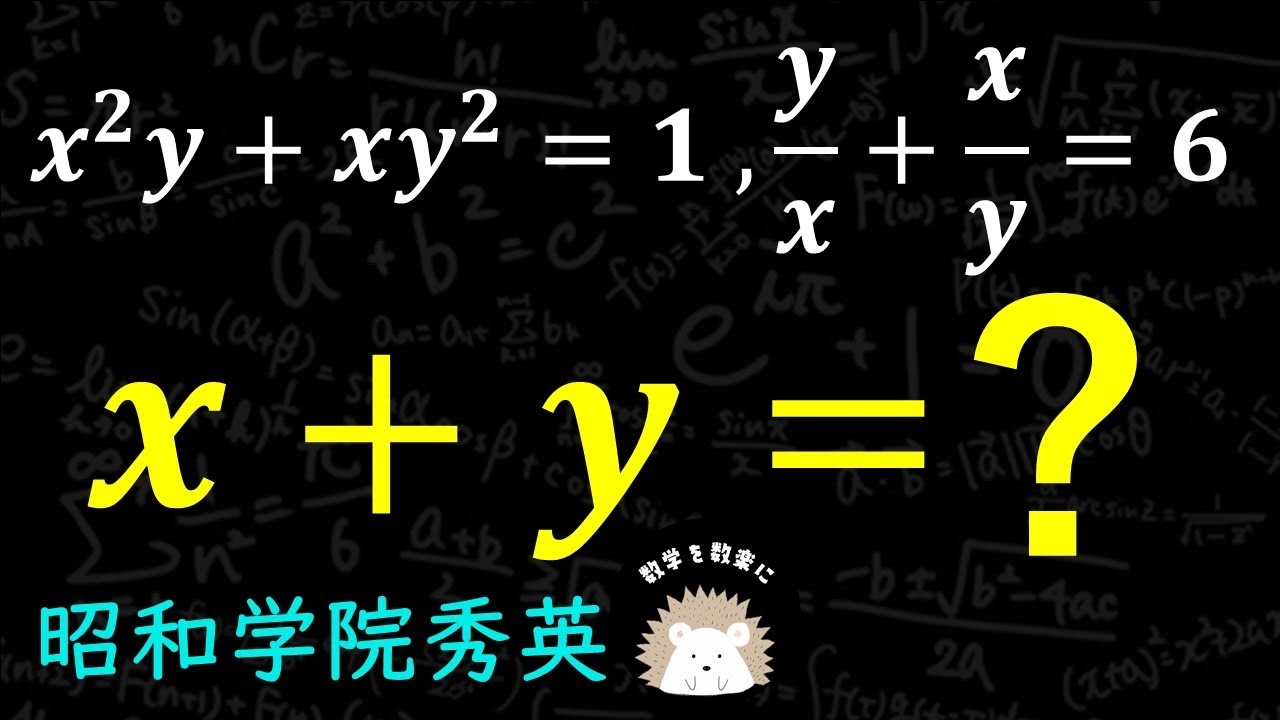
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2y+xy^2=1$ , $\frac{y}{x}+\frac{x}{y} = 6$のとき x+y=?
昭和学院秀英高等学校
この動画を見る
$x^2y+xy^2=1$ , $\frac{y}{x}+\frac{x}{y} = 6$のとき x+y=?
昭和学院秀英高等学校
気付けば、ほらそこに答えが
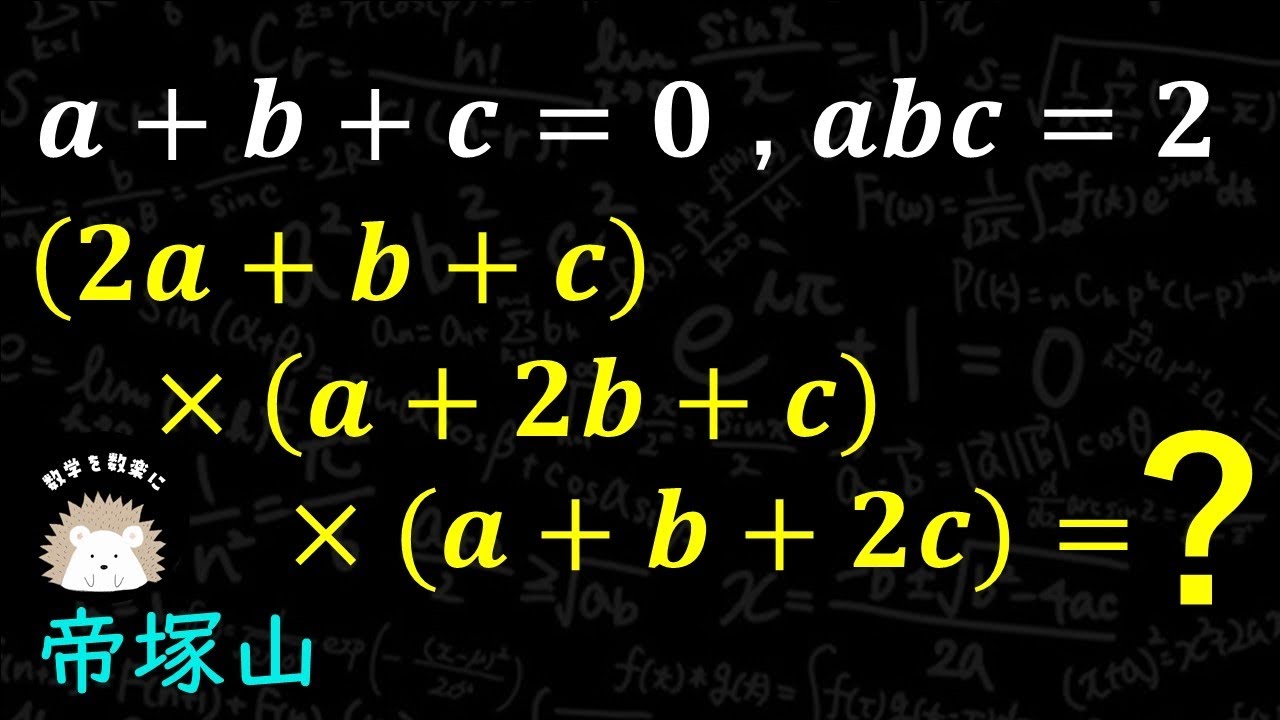
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a+b+c=0 , abc=2のとき
(2a+b+c)(a+2b+c)(a+b+2c)=
帝塚山高等学校
この動画を見る
a+b+c=0 , abc=2のとき
(2a+b+c)(a+2b+c)(a+b+2c)=
帝塚山高等学校
気づけば一瞬 海星
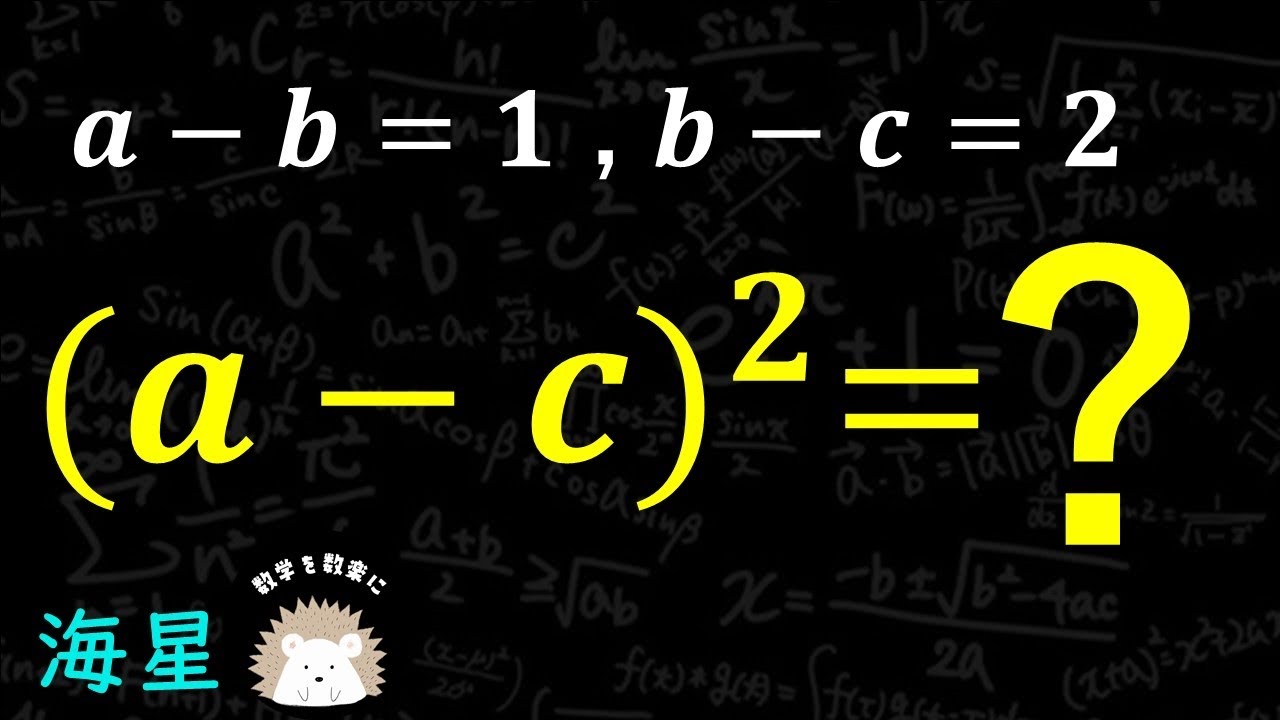
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a-b=1$ , $b-c = 2$ のとき
$(a-c)^2$=
海星高校
この動画を見る
$a-b=1$ , $b-c = 2$ のとき
$(a-c)^2$=
海星高校
【今見るべき公式集!】高校までに学ぶ「因数分解」の公式~全国入試問題解法

単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
中学校、高等学校までに学ぶ「因数分解の公式」一覧の解説
①$ma\pm mℓ=m(a \pm ℓ)$
②$x^2 \pm 2xy+y^2=(x \pm y)^2$
③$x^2-y^2=(x-y)(x+y)$
④$x^2 +(a+ℓ) x + aℓ=(x + a)(x+ℓ)$
⑤$acx^2+(ad+ℓc)x+ℓd=(ax+ℓ)(cx+d)$
⑥$x^3\pm y^3=(x+y)(x^2\mp xy+y^2)$
⑦$a^2+ℓ^2+c^2+2aℓ+2ℓc+2ca=(a+ℓ+c)^2$
⑧$a^3\pm 3a^2ℓ+3aℓ^2\pmℓ^3=(a \pmℓ)^3$
⑨$a^3+ℓ^3+c^3-3aℓc=(a+ℓ+c)(a^2+ℓ^2c^2-ℓc-ca-aℓ)$
この動画を見る
中学校、高等学校までに学ぶ「因数分解の公式」一覧の解説
①$ma\pm mℓ=m(a \pm ℓ)$
②$x^2 \pm 2xy+y^2=(x \pm y)^2$
③$x^2-y^2=(x-y)(x+y)$
④$x^2 +(a+ℓ) x + aℓ=(x + a)(x+ℓ)$
⑤$acx^2+(ad+ℓc)x+ℓd=(ax+ℓ)(cx+d)$
⑥$x^3\pm y^3=(x+y)(x^2\mp xy+y^2)$
⑦$a^2+ℓ^2+c^2+2aℓ+2ℓc+2ca=(a+ℓ+c)^2$
⑧$a^3\pm 3a^2ℓ+3aℓ^2\pmℓ^3=(a \pmℓ)^3$
⑨$a^3+ℓ^3+c^3-3aℓc=(a+ℓ+c)(a^2+ℓ^2c^2-ℓc-ca-aℓ)$
何をかけたら3乗になる?広陵

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
450をn倍するとある整数の3乗になった。
最も小さい自然数nは?
広陵高等学校
この動画を見る
450をn倍するとある整数の3乗になった。
最も小さい自然数nは?
広陵高等学校
【中学数学】展開と因数分解の最低限の点数稼ぎ~定期テストこれだけ~ 1-7【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5a+b+(8a^2-4ab)\div 4a$
2⃣
$(x+4y)^2$
3⃣
$(x+3)(x+7)$
4⃣
$(5a+2)(5a-2)$
5⃣
$x^2+9x+14$
6⃣
$2x^2-8x$
7⃣
$36-x^2$
8⃣
$x^2+16x+8$
この動画を見る
1⃣
$5a+b+(8a^2-4ab)\div 4a$
2⃣
$(x+4y)^2$
3⃣
$(x+3)(x+7)$
4⃣
$(5a+2)(5a-2)$
5⃣
$x^2+9x+14$
6⃣
$2x^2-8x$
7⃣
$36-x^2$
8⃣
$x^2+16x+8$
因数分解 東大寺学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a+1)^4-(4a^2+1)(a+1)^2+4a^2$を因数分解
東大寺学園高等学校
この動画を見る
$(a+1)^4-(4a^2+1)(a+1)^2+4a^2$を因数分解
東大寺学園高等学校
中学生の解き方 高校生の解き方
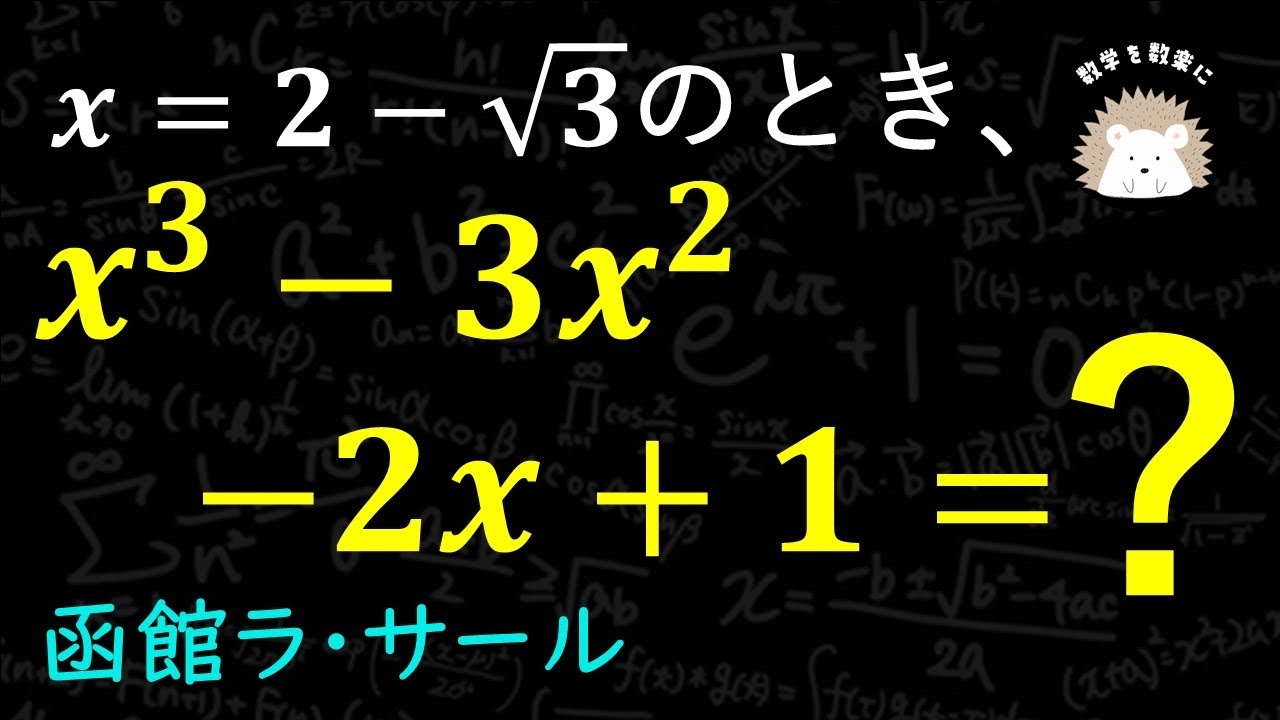
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2-\sqrt 3$のとき
$x^3-3x^2-2x+1$
函館ラ・サール高等学校
この動画を見る
$x=2-\sqrt 3$のとき
$x^3-3x^2-2x+1$
函館ラ・サール高等学校
【中学数学】因数分解の演習~特別な共通因数~ 1-6.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$ax-ay-2x+2y$
2⃣
$2x+2y+xz+yz$
3⃣
$xy^2-4x+2y^2-8$
この動画を見る
1⃣
$ax-ay-2x+2y$
2⃣
$2x+2y+xz+yz$
3⃣
$xy^2-4x+2y^2-8$
高校受験 数学 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$abc(abc-2c)-3c^2$を因数分解
城西大学付属川越高等学校
この動画を見る
$abc(abc-2c)-3c^2$を因数分解
城西大学付属川越高等学校
【中学数学】因数分解の演習~見落としがちな問題~ 1-6.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$4a^2bc-12ab^2c+8abc^2$
2⃣
$3ax^2-18ax+27a$
3⃣
$x^2+6xy+9y^2-25$
この動画を見る
1⃣
$4a^2bc-12ab^2c+8abc^2$
2⃣
$3ax^2-18ax+27a$
3⃣
$x^2+6xy+9y^2-25$
指数の計算 慶應義塾

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(-3)^{29} -3^{27}}{(\sqrt 3)^{50}}=$
慶應義塾高等学校
この動画を見る
$\frac{(-3)^{29} -3^{27}}{(\sqrt 3)^{50}}=$
慶應義塾高等学校
因数分解 函館ラ・サール

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^4(2x-3y)+27(9y-6x)$を因数分解
函館ラ・サール高等学校
この動画を見る
$x^4(2x-3y)+27(9y-6x)$を因数分解
函館ラ・サール高等学校
式の値 2通りの解説 函館ラ・サールB
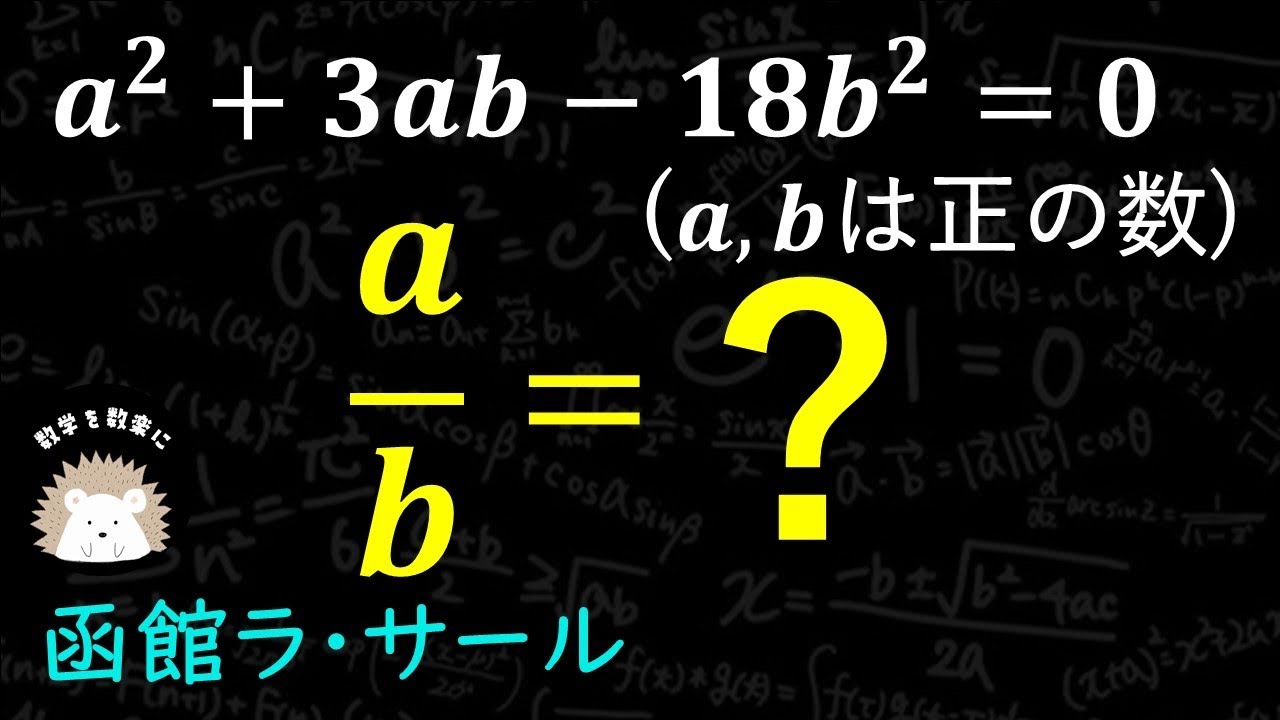
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2+3ab-18b^2=0(a>0,b>0)$
函館ラ・サール高等学校
この動画を見る
$a^2+3ab-18b^2=0(a>0,b>0)$
函館ラ・サール高等学校
【中学数学】分数の割り算・多項式の計算~計算ミスをなくす方法~ 1-2【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(12a^2-6a)\div \displaystyle \frac{2}{3}$
2⃣
$(\displaystyle \frac{2}{3}x^2y^2-\displaystyle \frac{4}{9}xy^2+2xy)\div(-\displaystyle \frac{2}{9}xy)$
3⃣
$(4x^3-6x^2+\displaystyle \frac{8}{5}x)\div(-\displaystyle \frac{4}{5}x)$
4⃣
$(-8a^2b+16ab)\div \displaystyle \frac{4}{5}a$
5⃣
$(4ab^2+5abc+\displaystyle \frac{1}{2})\div(\displaystyle \frac{7b}{5a})$
この動画を見る
1⃣
$(12a^2-6a)\div \displaystyle \frac{2}{3}$
2⃣
$(\displaystyle \frac{2}{3}x^2y^2-\displaystyle \frac{4}{9}xy^2+2xy)\div(-\displaystyle \frac{2}{9}xy)$
3⃣
$(4x^3-6x^2+\displaystyle \frac{8}{5}x)\div(-\displaystyle \frac{4}{5}x)$
4⃣
$(-8a^2b+16ab)\div \displaystyle \frac{4}{5}a$
5⃣
$(4ab^2+5abc+\displaystyle \frac{1}{2})\div(\displaystyle \frac{7b}{5a})$
【中学数学】因数分解の演習~一緒に解こう~ 1-6.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(x+3)-2(x+3)^2$
2⃣
$(x+y)^2-(x+y)-12$
3⃣
$x^2(a+b)-4x(a+b)+4(a+b)$
この動画を見る
1⃣
$(x+3)-2(x+3)^2$
2⃣
$(x+y)^2-(x+y)-12$
3⃣
$x^2(a+b)-4x(a+b)+4(a+b)$
因数分解 2通りの解説

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^2-15x)+(x^2-225)+(x^2+2x-255)$を因数分解せよ。
函館ラ・サール
この動画を見る
$(x^2-15x)+(x^2-225)+(x^2+2x-255)$を因数分解せよ。
函館ラ・サール
指数の計算 函館ラ・サール B
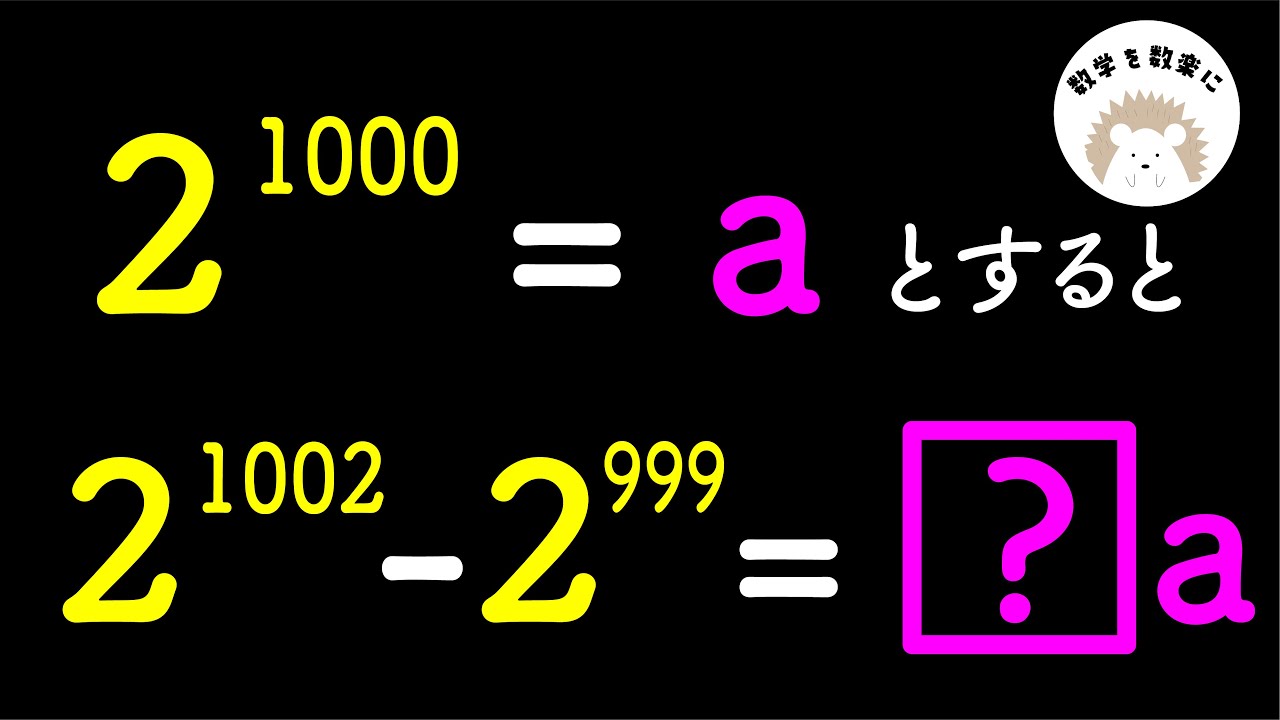
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{1000}=a$とすると
$2^{1002} - 2^{999}=\boxed{?}a$
函館ラ・サール
この動画を見る
$2^{1000}=a$とすると
$2^{1002} - 2^{999}=\boxed{?}a$
函館ラ・サール
素因数分解 教えて下さい たくさんのコメントありがとうございます。

因数分解 伝えたいことはただ一つ

言いたいことはただ一つ

式の値 慶應女子 B
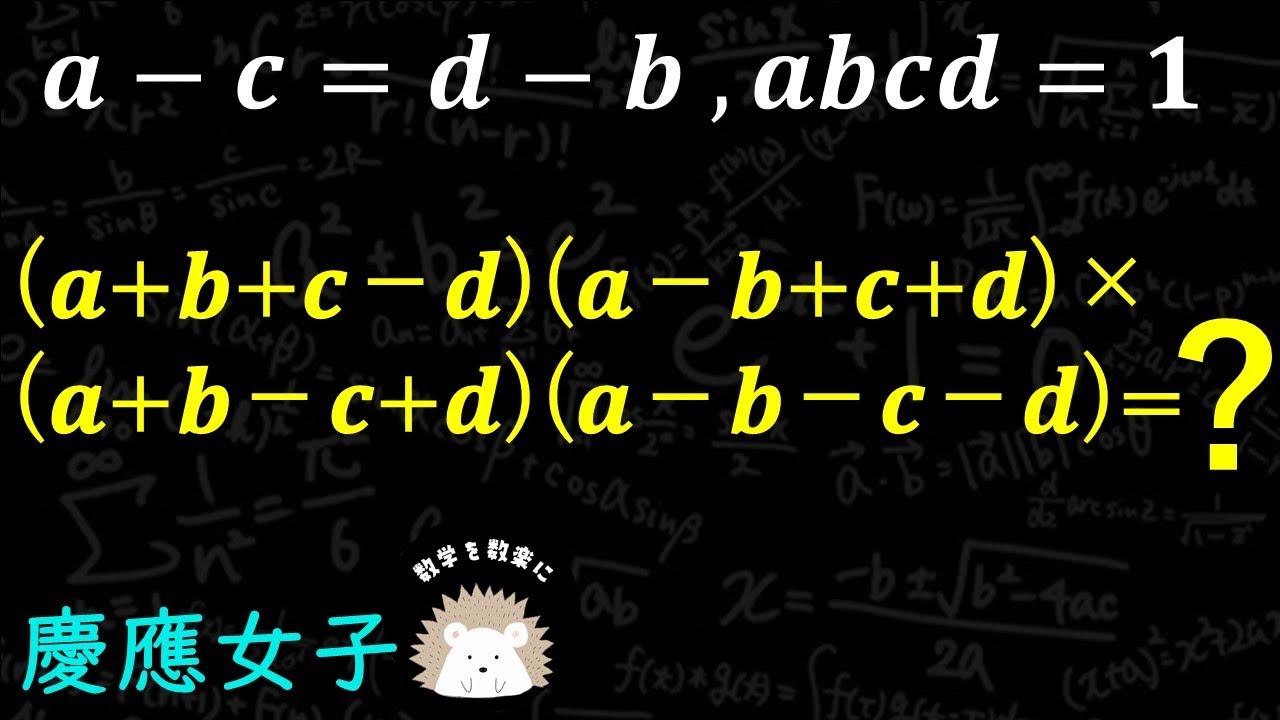
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a-c=d-b,abcd=1のとき
(a+b+c-d)(a-b+c+d)(a+b-c+d)(a-b-c-d)
慶應義塾女子高等学校
この動画を見る
a-c=d-b,abcd=1のとき
(a+b+c-d)(a-b+c+d)(a+b-c+d)(a-b-c-d)
慶應義塾女子高等学校
気づけば一瞬 式の値 久留米大附設
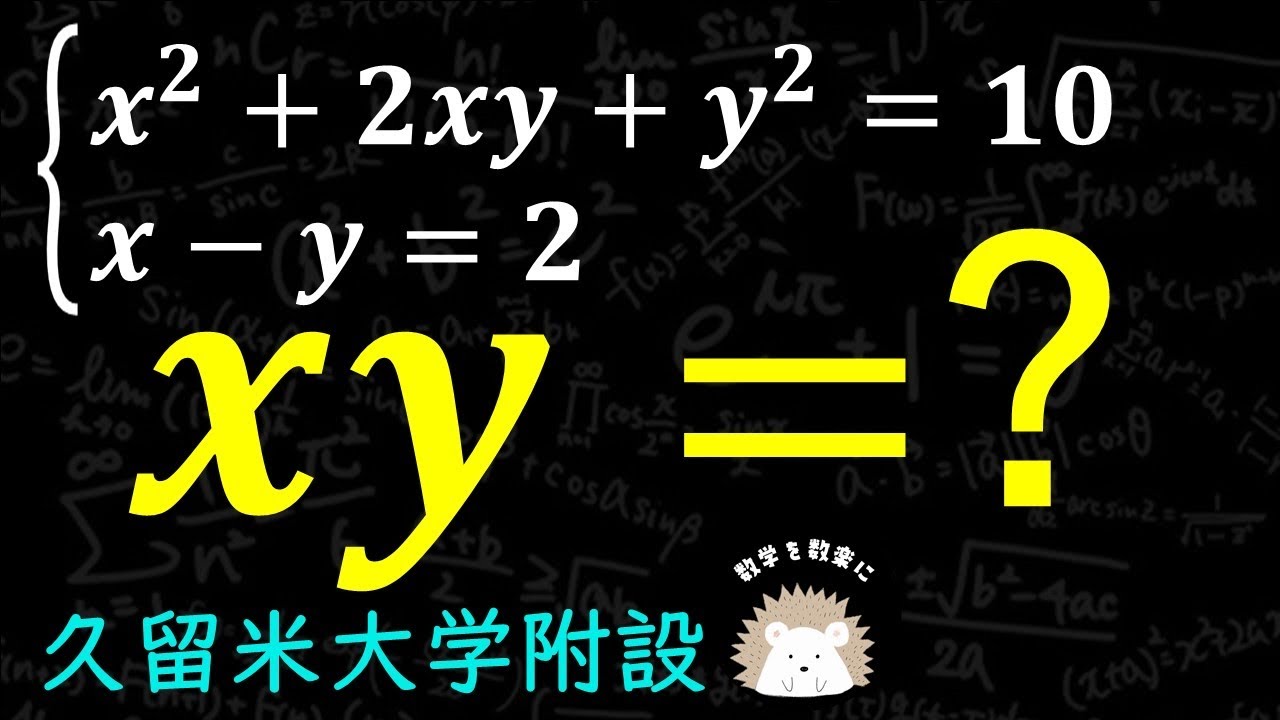
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 2xy +y^2 = 10 \\
x - y = 2
\end{array}
\right.
\end{eqnarray}
$
$xy=$
久留米大附設高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 + 2xy +y^2 = 10 \\
x - y = 2
\end{array}
\right.
\end{eqnarray}
$
$xy=$
久留米大附設高等学校
因数分解 大阪星光学院

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$4x^2(x-3)^2+11(x^2-3x)-3$を因数分解
大阪星光学院高等学校
この動画を見る
$4x^2(x-3)^2+11(x^2-3x)-3$を因数分解
大阪星光学院高等学校
慶應女子 式の値
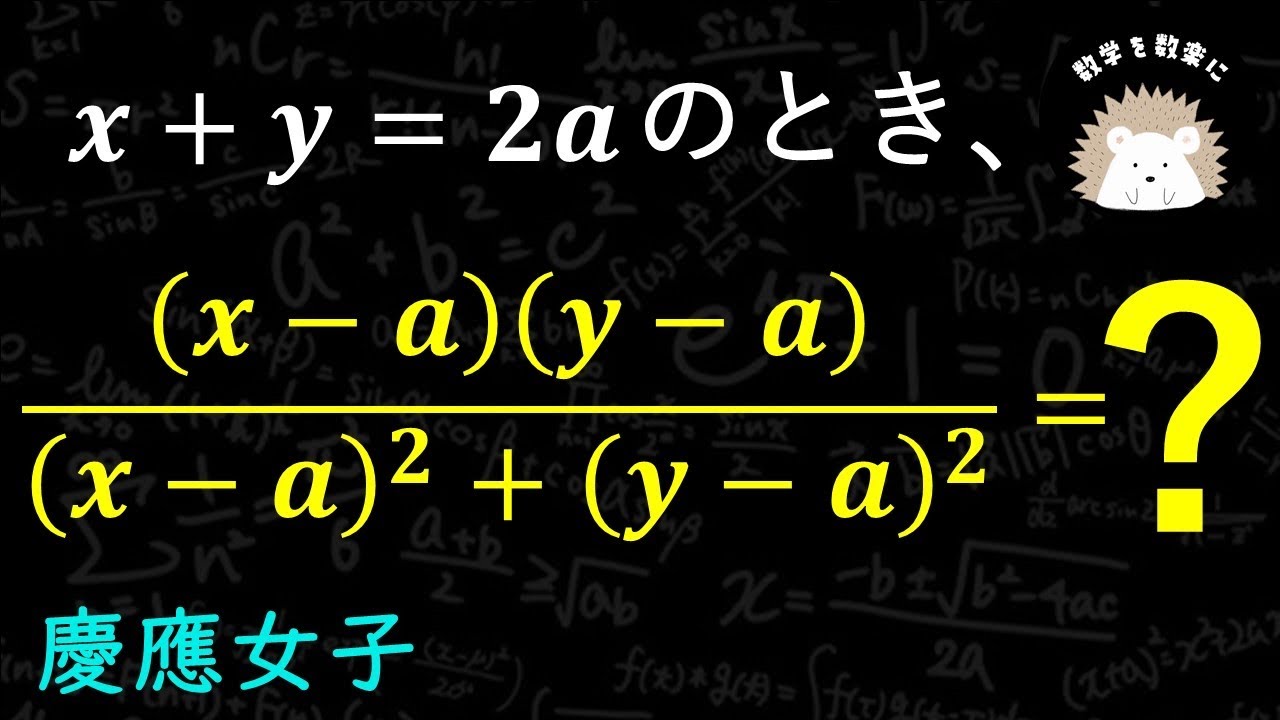
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y=2a$のとき
$\frac{(x-a)(y-a)}{(x-a)^2+(y-a)^2}$
慶應義塾女子高等学校
この動画を見る
$x+y=2a$のとき
$\frac{(x-a)(y-a)}{(x-a)^2+(y-a)^2}$
慶應義塾女子高等学校
因数分解 芝浦工大柏

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2-b^2-4c^2-6a+4bc+9$を因数分解せよ。
芝浦工業大学柏高等学校
この動画を見る
$a^2-b^2-4c^2-6a+4bc+9$を因数分解せよ。
芝浦工業大学柏高等学校
中学生も解ける!挑戦あれ!

解いたらわかるこの気持ち