平方根
平方根
【中学数学】平方根の基礎固め【中３夏期講習④】
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
問1 次の数の平方根を求めよ。
(1)$4$ (2)$49$ (3)$7$ (4) ${(-8)}^2$ (5)$x^6$
問2 次の計算をしなさい
(1)$\sqrt{6}\times\sqrt{30}$ (2)$6\sqrt{10}\div3\sqrt{2}$ (3)$2(\sqrt{3}+2\sqrt{2})-(3\sqrt{2}-\sqrt{2})$
(4)$\sqrt{\frac{3}{2}}+\frac{2\sqrt{6}}{3}-\sqrt{\frac{8}{3}}$ (5)$12\sqrt{60}\div 3\sqrt{10}$ (6)$2\sqrt{3}\times 3\sqrt{2}+\frac{12}{\sqrt{6}}$
この動画を見る
問1 次の数の平方根を求めよ。
(1)$4$ (2)$49$ (3)$7$ (4) ${(-8)}^2$ (5)$x^6$
問2 次の計算をしなさい
(1)$\sqrt{6}\times\sqrt{30}$ (2)$6\sqrt{10}\div3\sqrt{2}$ (3)$2(\sqrt{3}+2\sqrt{2})-(3\sqrt{2}-\sqrt{2})$
(4)$\sqrt{\frac{3}{2}}+\frac{2\sqrt{6}}{3}-\sqrt{\frac{8}{3}}$ (5)$12\sqrt{60}\div 3\sqrt{10}$ (6)$2\sqrt{3}\times 3\sqrt{2}+\frac{12}{\sqrt{6}}$
【中学数学あるある】式変形で気持ち良く解ける計算問題 #Shorts
単元：
#数学(中学生)#中３数学#平方根
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$\sqrt{85^2-84^2+61^2-60^2-26×11}$
これを解け。
この動画を見る
$\sqrt{85^2-84^2+61^2-60^2-26×11}$
これを解け。
【手を動かせ！別解を探せ！】文字式：洛南高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x=-1+\sqrt5$のとき,$(x-1)x+x(x+1)-(x-2)x$の値を求めなさい.
洛南高校過去問
この動画を見る
$x=-1+\sqrt5$のとき,$(x-1)x+x(x+1)-(x-2)x$の値を求めなさい.
洛南高校過去問
高校受験と授業参観にワンポイント・アドバイス！～全国入試問題解法 #Shorts #数学 #受験対策
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
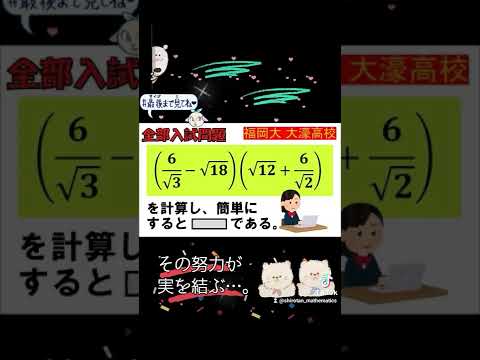
$ \left(\dfrac{6}{\sqrt3}-\sqrt{18}\right)\left(\sqrt{12}+\dfrac{6}{\sqrt2}\right)$を計算せよ.
この動画を見る
$ \left(\dfrac{6}{\sqrt3}-\sqrt{18}\right)\left(\sqrt{12}+\dfrac{6}{\sqrt2}\right)$を計算せよ.
平方数 九州学院（熊本）
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$20(3n+6)$がある整数の平方になる最小の自然数nを求めよ。
九州学院高等学校
この動画を見る
$20(3n+6)$がある整数の平方になる最小の自然数nを求めよ。
九州学院高等学校
【上手いやり方などと自慢するなかれ…！】平方根：愛知県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(\sqrt5+\sqrt2)^2-(\sqrt5-\sqrt2)^2$を計算しなさい.
愛知県公立高等学校過去問
この動画を見る
$(\sqrt5+\sqrt2)^2-(\sqrt5-\sqrt2)^2$を計算しなさい.
愛知県公立高等学校過去問
入試で必須の計算を15秒で習得する動画～全国入試問題解法 #Shorts #入試問題
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
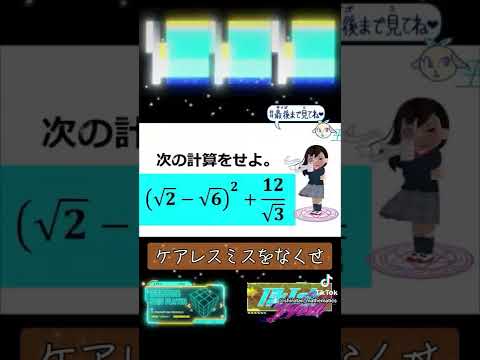
$(\sqrt2-\sqrt6)^2+\dfrac{12}{\sqrt3}$を計算せよ.
この動画を見る
$(\sqrt2-\sqrt6)^2+\dfrac{12}{\sqrt3}$を計算せよ.
30秒で高校入試の必出問題を身に付ける動画～全国入試問題解法 #Shorts #高校入試
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
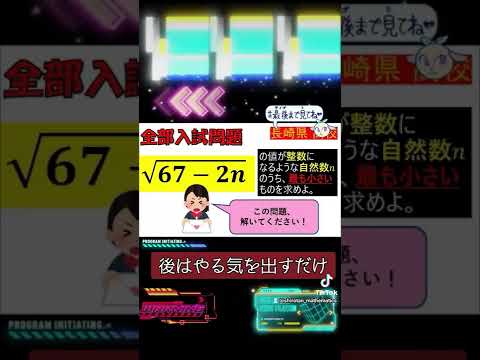
$\sqrt{67-2n}$の値が整数であるとき,最も小さい$n$を求めよ.($n$は自然数)
この動画を見る
$\sqrt{67-2n}$の値が整数であるとき,最も小さい$n$を求めよ.($n$は自然数)
あなたならどう説明しますか？
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\sqrt{ 2 }+\sqrt{ 3 }=\sqrt{ 5 }$にならない理由説明動画です
この動画を見る
$\sqrt{ 2 }+\sqrt{ 3 }=\sqrt{ 5 }$にならない理由説明動画です
数学のエッセンスを0.5分に詰め込んだ動画～全国入試問題解法 #Shorts #数学
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
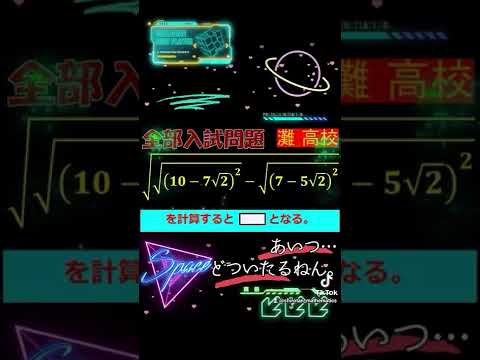
$\sqrt{\sqrt{(10-7\sqrt2)}^2-\sqrt{(7-5\sqrt2)^2}}$の値を求めよ.
この動画を見る
$\sqrt{\sqrt{(10-7\sqrt2)}^2-\sqrt{(7-5\sqrt2)^2}}$の値を求めよ.
15秒で数学の1問を身に付ける動画～全国入試問題解法 #Shorts #数学
単元：
#数学(中学生)#中３数学#平方根
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
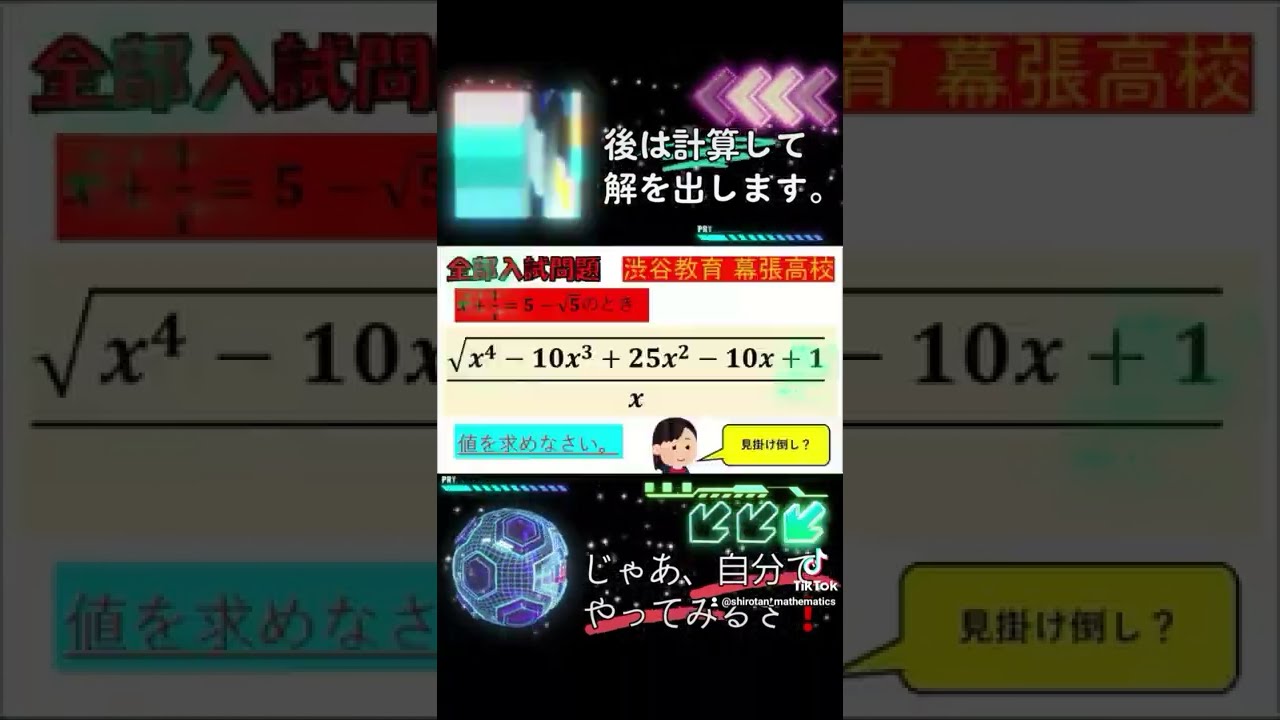
$x+\dfrac{1}{x}=5-\sqrt5$のとき,$\dfrac{\sqrt{x^4-10x^3+25x^2-10x+1}}{x}$の値を求めよ.
この動画を見る
$x+\dfrac{1}{x}=5-\sqrt5$のとき,$\dfrac{\sqrt{x^4-10x^3+25x^2-10x+1}}{x}$の値を求めよ.
【無理数とは！】平方根（有理数と無理数）後編：教科書順で内容確認～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
平方根（有理数と無理数）に関して解説していきます.
この動画を見る
平方根（有理数と無理数）に関して解説していきます.
【中学数学】平方根・ルートの足し算が中１でも理解できます 2-4【中３数学】
単元：
#数学(中学生)#中３数学#平方根
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\displaystyle
\sqrt{2}+\sqrt{3}=\sqrt{5}
$ にならない理由
この動画を見る
$\displaystyle
\sqrt{2}+\sqrt{3}=\sqrt{5}
$ にならない理由
【有理数とは！】平方根（有理数と無理数）前編：教科書順で内容確認～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
平方根（有理数と無理数）に関して解説していきます.
この動画を見る
平方根（有理数と無理数）に関して解説していきます.
【この形！どの形？】平方根：渋谷教育学園幕張高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
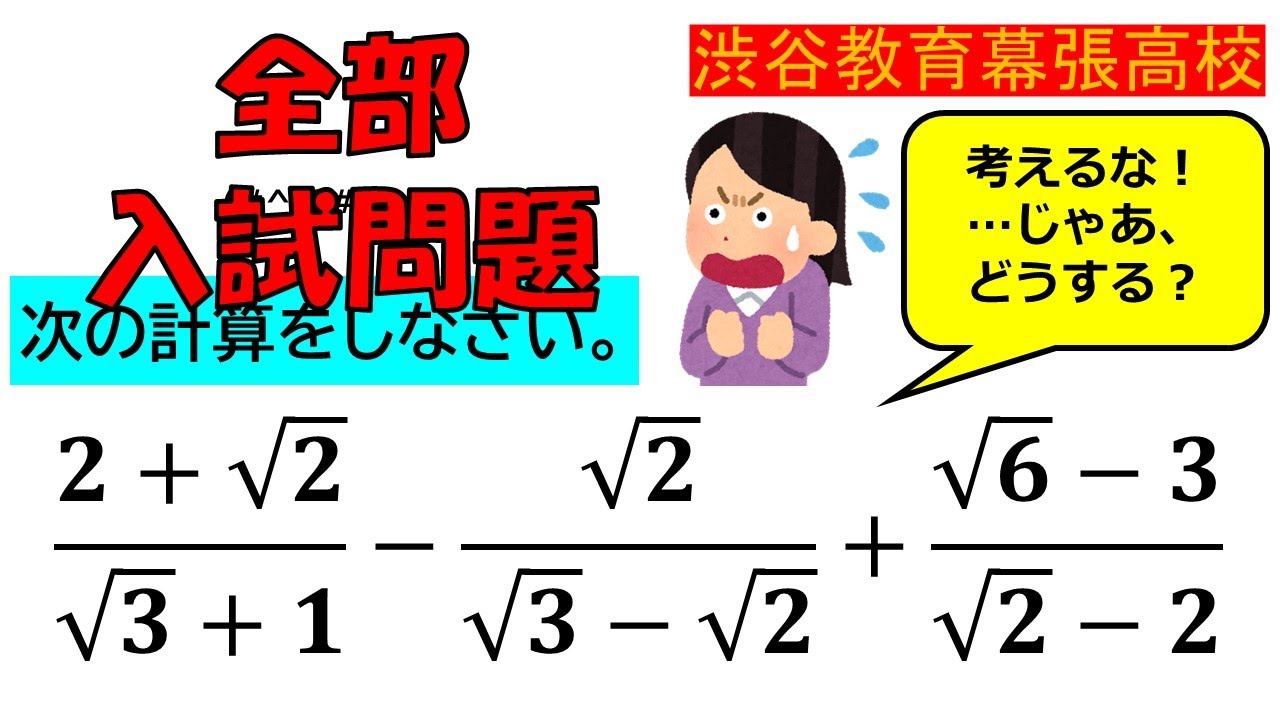
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
この動画を見る
次の計算をしなさい.
$\dfrac{2+\sqrt2}{\sqrt3+1}-\dfrac{\sqrt2}{\sqrt3-\sqrt2}+\dfrac{\sqrt6-3}{\sqrt2-2}$
渋谷教育学園幕張高等学校過去問
整数と分数では世界表せないよね？
【数学検定】数学検定3級対策問題1
単元：
#数学(中学生)#中１数学#中２数学#中３数学#正の数・負の数#式の計算（単項式・多項式・式の四則計算）#平方根#数学検定・数学甲子園・数学オリンピック等#文字と式#数学検定#数学検定3級
指導講師：
理数個別チャンネル
問題文全文(内容文)：
数学検定3級対策問題1の解説動画です。
問題１.次の計算をしなさい。
(1) 9－(－5)＋(－8)
(2) 24－16÷(－4)
(3) 2³＋(－3)²
(4) 35/36 ÷ (－2/9) × 4/7
(5) √125－√45＋√20
(6) (√3＋4)²－24/√3
(7) 3(3ｘ＋5)＋4(2ｘ－7)
(8) 0.5(6ｘ－1)－0.8(3ｘ－4)
(9) 7(4ｘ－5ｙ)－2(9ｘ＋y)
(10) 3ｘ－6ｙ/8 － 2ｘ－7ｙ/12
(11) －5ｘ²ｙ × 9ｘ²ｙ²
(12) 13ｘ³ｙ²/5 ÷ (－4ｘ²ｙ/5) × (－2ｘｙ²/13)
この動画を見る
数学検定3級対策問題1の解説動画です。
問題１.次の計算をしなさい。
(1) 9－(－5)＋(－8)
(2) 24－16÷(－4)
(3) 2³＋(－3)²
(4) 35/36 ÷ (－2/9) × 4/7
(5) √125－√45＋√20
(6) (√3＋4)²－24/√3
(7) 3(3ｘ＋5)＋4(2ｘ－7)
(8) 0.5(6ｘ－1)－0.8(3ｘ－4)
(9) 7(4ｘ－5ｙ)－2(9ｘ＋y)
(10) 3ｘ－6ｙ/8 － 2ｘ－7ｙ/12
(11) －5ｘ²ｙ × 9ｘ²ｙ²
(12) 13ｘ³ｙ²/5 ÷ (－4ｘ²ｙ/5) × (－2ｘｙ²/13)
【簡潔に予習・復習！】平方根（意味と計算）：教科書順で内容確認～全国入試問題解法
平方根のめんどくさーい計算 大阪星光学院
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
この動画を見る
$x= \frac{3 + \sqrt {11}}{2}$ , $y= \frac{3- \sqrt{11}}{2}$
$\frac{x^4-y^4}{12} =?$
大阪星光学院高等学校
ルート含む数の大小関係 青山学院
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の数を小さい順に並べ記号で答えよ
ア. $\frac{7}{6}$
イ. $\frac{\sqrt {10}}{3}$
ウ. $\sqrt{\frac{7}{6}}$
エ. $\frac{\sqrt5}{2}$
青山学院大学高等部
この動画を見る
次の数を小さい順に並べ記号で答えよ
ア. $\frac{7}{6}$
イ. $\frac{\sqrt {10}}{3}$
ウ. $\sqrt{\frac{7}{6}}$
エ. $\frac{\sqrt5}{2}$
青山学院大学高等部
【正解するのが一番の目的！】平方根：東京都立八王子東高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\left(\dfrac{\sqrt6+2}{\sqrt2}\right)\left(\dfrac{\sqrt2-\sqrt3}{3}\right)$を計算せよ.
都立八王子東高校過去問
この動画を見る
$\left(\dfrac{\sqrt6+2}{\sqrt2}\right)\left(\dfrac{\sqrt2-\sqrt3}{3}\right)$を計算せよ.
都立八王子東高校過去問
サクサク解こう
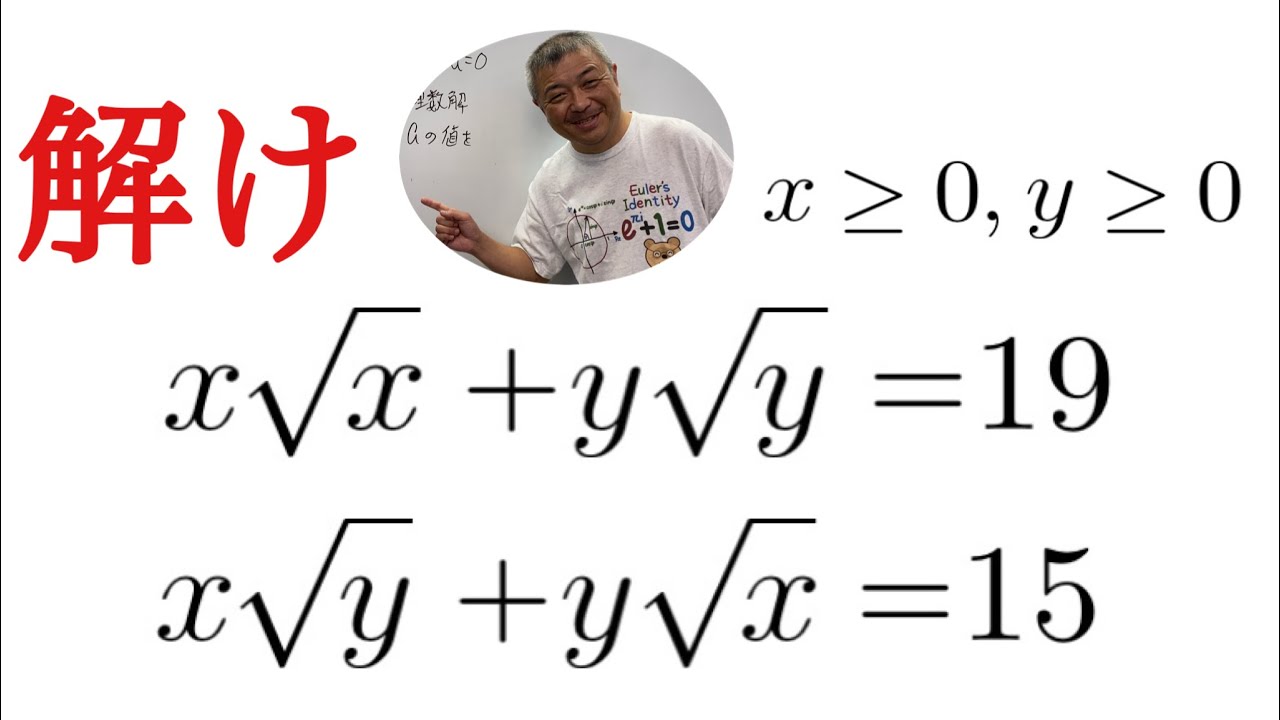
単元：
#平方根#数と式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x \geqq 0,y \geqq 0$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=19 \\
x\sqrt y+y\sqrt x=15
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$ x \geqq 0,y \geqq 0$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x\sqrt x+y\sqrt y=19 \\
x\sqrt y+y\sqrt x=15
\end{array}
\right.
\end{eqnarray}$
これを解け.
ルートのかけ算
どうやったら簡単に解けるか 2022 立命館高校
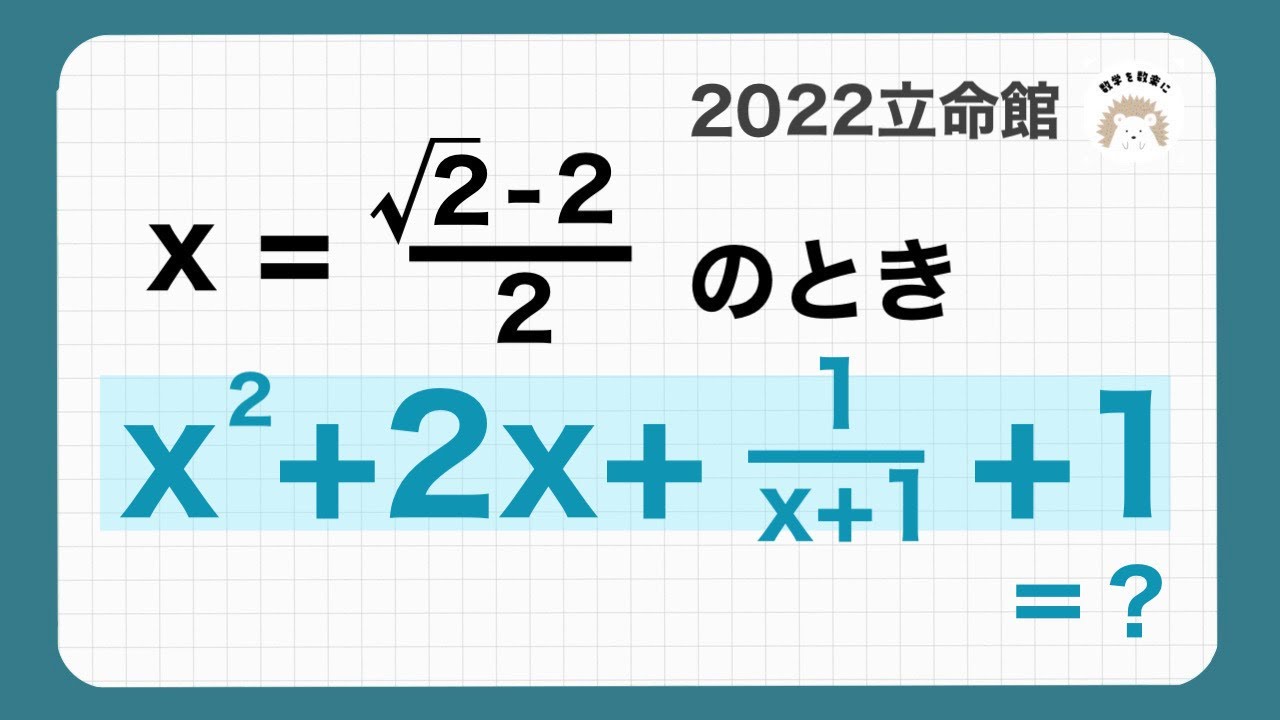
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x=\frac{\sqrt 2 -2}{2}$のとき
$x^2+2x+ \frac{1}{x+1} +1 =?$
2022立命館高等学校
この動画を見る
$x=\frac{\sqrt 2 -2}{2}$のとき
$x^2+2x+ \frac{1}{x+1} +1 =?$
2022立命館高等学校
動体視力と数学を鍛える30秒の誘い（いざない）～全国入試問題解法 #Shorts
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(\sqrt3+\sqrt5)^2$の小数部分を$x$とするとき,
$x^2+14x$の値を求めよ.
慶応志木高校過去問
この動画を見る
$(\sqrt3+\sqrt5)^2$の小数部分を$x$とするとき,
$x^2+14x$の値を求めよ.
慶応志木高校過去問
これできた？
これ分かる？
これ解ける？
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$\sqrt{ 2022 \sqrt{ 2021 \times 2019 + 1 + 1 } }$
値を求めよ
この動画を見る
$\sqrt{ 2022 \sqrt{ 2021 \times 2019 + 1 + 1 } }$
値を求めよ
平方根の計算 城北高校 2022年入試問題解説52問目
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
この動画を見る
$\sqrt{2023 \times 2021 - 4044 +2}$
2022城北高等学校
令和4年度 灘高校の最初の一問 2022年入試問題解説47問目
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校
この動画を見る
$(\sqrt {2022} + \sqrt {77})^2
-2(\sqrt {2022} + \sqrt {77})(\sqrt {2022} - 1)
+2(\sqrt {2022} - \sqrt {77})(\sqrt {2022} - 1)
-(\sqrt {2022} - \sqrt {77})^2
$
2022灘高等学校