 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
中1数学「度数分布多角形(度数折れ線)」【毎日配信】

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第67回度数分布多角形~
例題
次の図はあるクラス24人の英語と数学のテスト結果を 度数分布多角形で表したものです。
次の階級の相対度数を小教第2位までで求めなさい。
(1)英語60点以上80点未満
(2)数学20点以上40点未満
この動画を見る
中1~第67回度数分布多角形~
例題
次の図はあるクラス24人の英語と数学のテスト結果を 度数分布多角形で表したものです。
次の階級の相対度数を小教第2位までで求めなさい。
(1)英語60点以上80点未満
(2)数学20点以上40点未満
中1数学「ヒストグラム(柱状グラフ)」【毎日配信】

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第66回ヒストグラム~
例題
次の表は、ある中学校のクラスの体重を、ヒストグラムで 表したものです。
(1)階級の幅は何kgですか。
(2) 50kgの生徒は、重い方から数えて 何番目から何番目の間にいますか。
(3) 48kg以上52kg未満の相対度数を 求めなさい。
(4) 40kg未満の相対度数を求めなさい。
この動画を見る
中1~第66回ヒストグラム~
例題
次の表は、ある中学校のクラスの体重を、ヒストグラムで 表したものです。
(1)階級の幅は何kgですか。
(2) 50kgの生徒は、重い方から数えて 何番目から何番目の間にいますか。
(3) 48kg以上52kg未満の相対度数を 求めなさい。
(4) 40kg未満の相対度数を求めなさい。
【中学数学】平面図形の移動・演習~岡山県公立高校入試2019年~【高校受験】
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#岡山県公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
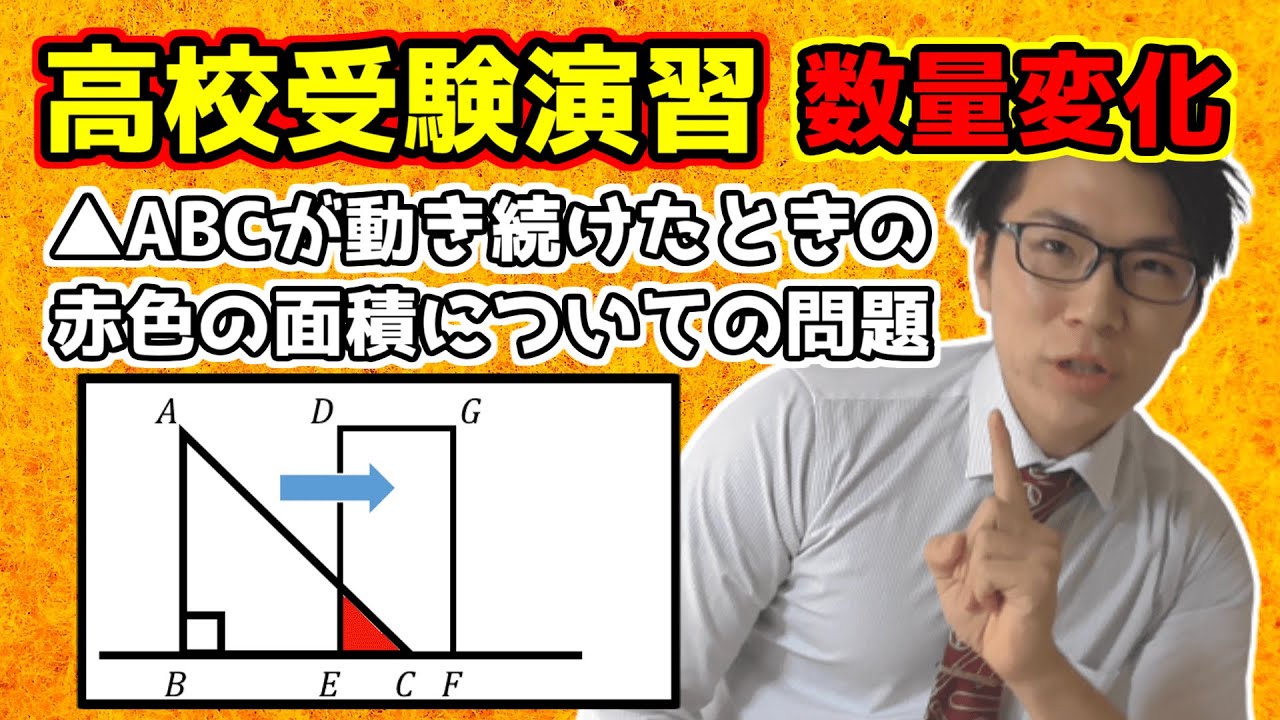
【岡山県公立高校入試2019年】平面図形の移動・演習
この動画を見る
【岡山県公立高校入試2019年】平面図形の移動・演習
中1数学「度数分布表と相対度数」【毎日配信】
単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第65回度数分布表と相対度数~
例題
次の表は、ある中学校50人のハンドボール投げの 記録を度数分布表に整理したものです。
(1) 階級の幅は何mですか。
(2)表のアにあてはまる数を求めなさい。
(3) 記録がよくない方から数えて8番目の人は。 どの階級に入りますか。
(4)21m以上24m未満の相対度数を求めなさい。
(5) 15m未満の相対度数を求めなさい。
この動画を見る
中1~第65回度数分布表と相対度数~
例題
次の表は、ある中学校50人のハンドボール投げの 記録を度数分布表に整理したものです。
(1) 階級の幅は何mですか。
(2)表のアにあてはまる数を求めなさい。
(3) 記録がよくない方から数えて8番目の人は。 どの階級に入りますか。
(4)21m以上24m未満の相対度数を求めなさい。
(5) 15m未満の相対度数を求めなさい。
2021入試予想問題~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2021入試予想問題~全国入試問題解法
次の入試問題を解け。
$2021 = 43 × 47$
①$2025=45^2$であることを
利用して $2021$の約数を求めよ。
②$2025=45^2$であることを
利用して $2021$の約数を求めよ。
③以下の式を計算せよ
$2025^2+2020 \times 2021-4041 \times 2025$
④$2001+2002+2003+....+2021$
を計算せよ。
⑤$a,ℓ$:自然数、$a$を$ℓ$で割った余り$R_{ℓ}(a)$
(1)$R_{40} (2021), R_{40} (2021^2)$を求めよ。
(2)$R_{40} (2021^{2021})$を求めよ。
⑥ある整数$x$を$12$で割ると、
余りろとなりました。
このとき、$x$を$2021$倍した
$2021x$を$12$で割った余りを求めよ。
⑦ $3^{2021}$の一の位の数を求めなさい。
この動画を見る
2021入試予想問題~全国入試問題解法
次の入試問題を解け。
$2021 = 43 × 47$
①$2025=45^2$であることを
利用して $2021$の約数を求めよ。
②$2025=45^2$であることを
利用して $2021$の約数を求めよ。
③以下の式を計算せよ
$2025^2+2020 \times 2021-4041 \times 2025$
④$2001+2002+2003+....+2021$
を計算せよ。
⑤$a,ℓ$:自然数、$a$を$ℓ$で割った余り$R_{ℓ}(a)$
(1)$R_{40} (2021), R_{40} (2021^2)$を求めよ。
(2)$R_{40} (2021^{2021})$を求めよ。
⑥ある整数$x$を$12$で割ると、
余りろとなりました。
このとき、$x$を$2021$倍した
$2021x$を$12$で割った余りを求めよ。
⑦ $3^{2021}$の一の位の数を求めなさい。
角度を求める C 日大桜ヶ丘
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
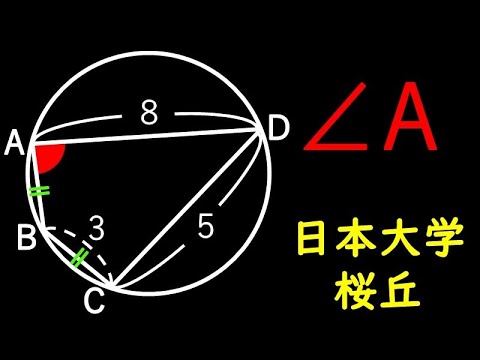
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
この動画を見る
$\angle A=?$
*図は動画内参照
日本大学櫻丘高等学校
【高校受験対策/数学】関数52

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数52
Q
太郎さんが所属するサッカー部で、オリジナルタオルを作ることになり、かかる費用を調べたところ、A店とB店の料金はそれぞれ表1、表2のようになっていた。
また、右の図はA店で タオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$x$と$y$の関係をグラフに 表したものである。
ただし、このグラフで端の点をふくむ場合は●、ふくまない場合は○で表している。
ただし、消費税は考えないものとする。
【表1】 A店の料金
枚数によって、金額は次の通りです。
・20枚までは何枚でも、3500円
・21枚から50枚までは何枚でも6500円
・51枚から80枚までは何枚でも9000円
【表2】 B店の料金
注文の時に初期費用として3000円かかり、それに加えてタオル1枚につき100円かかります。
①B店でタオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$y$を$x$の式で表しなさい。
②A店、B店でそれぞれタオルを30枚作るとき、かかる費用はどちらの店がいくら安いか求めなさい。
③タオルを作る枚数を40枚から80枚までとしたとき、B店で作るときにかかる費用がA店で作るときにかかる費用よりも安くなるのは、何枚以上何枚以下のときか求めなさい。
この動画を見る
高校受験対策・関数52
Q
太郎さんが所属するサッカー部で、オリジナルタオルを作ることになり、かかる費用を調べたところ、A店とB店の料金はそれぞれ表1、表2のようになっていた。
また、右の図はA店で タオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$x$と$y$の関係をグラフに 表したものである。
ただし、このグラフで端の点をふくむ場合は●、ふくまない場合は○で表している。
ただし、消費税は考えないものとする。
【表1】 A店の料金
枚数によって、金額は次の通りです。
・20枚までは何枚でも、3500円
・21枚から50枚までは何枚でも6500円
・51枚から80枚までは何枚でも9000円
【表2】 B店の料金
注文の時に初期費用として3000円かかり、それに加えてタオル1枚につき100円かかります。
①B店でタオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$y$を$x$の式で表しなさい。
②A店、B店でそれぞれタオルを30枚作るとき、かかる費用はどちらの店がいくら安いか求めなさい。
③タオルを作る枚数を40枚から80枚までとしたとき、B店で作るときにかかる費用がA店で作るときにかかる費用よりも安くなるのは、何枚以上何枚以下のときか求めなさい。
円と角度 慶應女子B
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
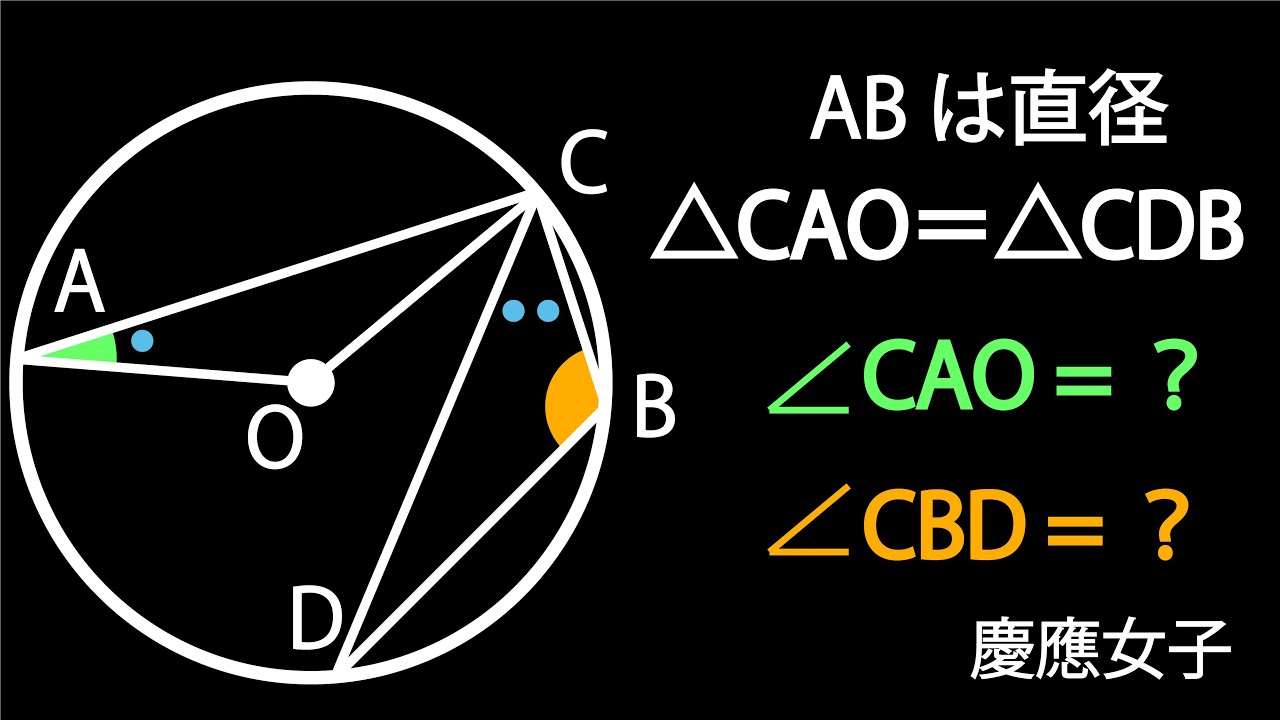
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
この動画を見る
△CAO=△CDB
$\angle CAO = ?$
$\angle CBD = ?$
*図は動画内参照
慶應義塾女子高等学校
図形:日本大学第二高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
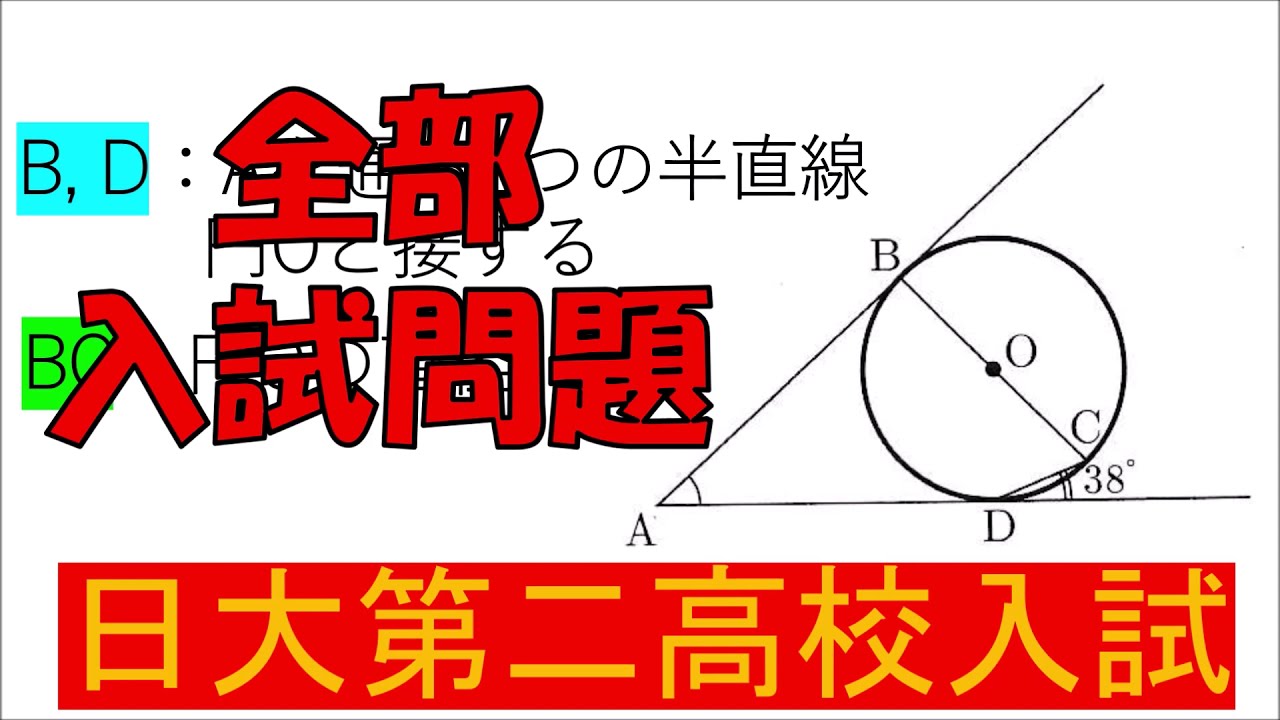
入試問題 日本大学第二高等学校
$B, D:A$を通る$2$つの半直線
円$O$と接する
$BC:$円$O$の直径
$\angle BAD$の大きさを求めよ。
※図は動画内参照
この動画を見る
入試問題 日本大学第二高等学校
$B, D:A$を通る$2$つの半直線
円$O$と接する
$BC:$円$O$の直径
$\angle BAD$の大きさを求めよ。
※図は動画内参照
【中学数学】確率の演習~山口県公立高校入試2019~【高校受験】

中1数学「円錐の側面の中心角」【毎日配信】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第64回円錐の側面の中心角~
例題
ある円錐を展開図に表したら、次の図のように なりました。
(1) 底面の円の半径が9cmのとき、 おうぎ形の中心角は何度ですか。
(2)おうぎ形の中心角が120度のとき、 底面の円の半径は何cmですか。
この動画を見る
中1~第64回円錐の側面の中心角~
例題
ある円錐を展開図に表したら、次の図のように なりました。
(1) 底面の円の半径が9cmのとき、 おうぎ形の中心角は何度ですか。
(2)おうぎ形の中心角が120度のとき、 底面の円の半径は何cmですか。
円と三平方 中央大附属 C
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
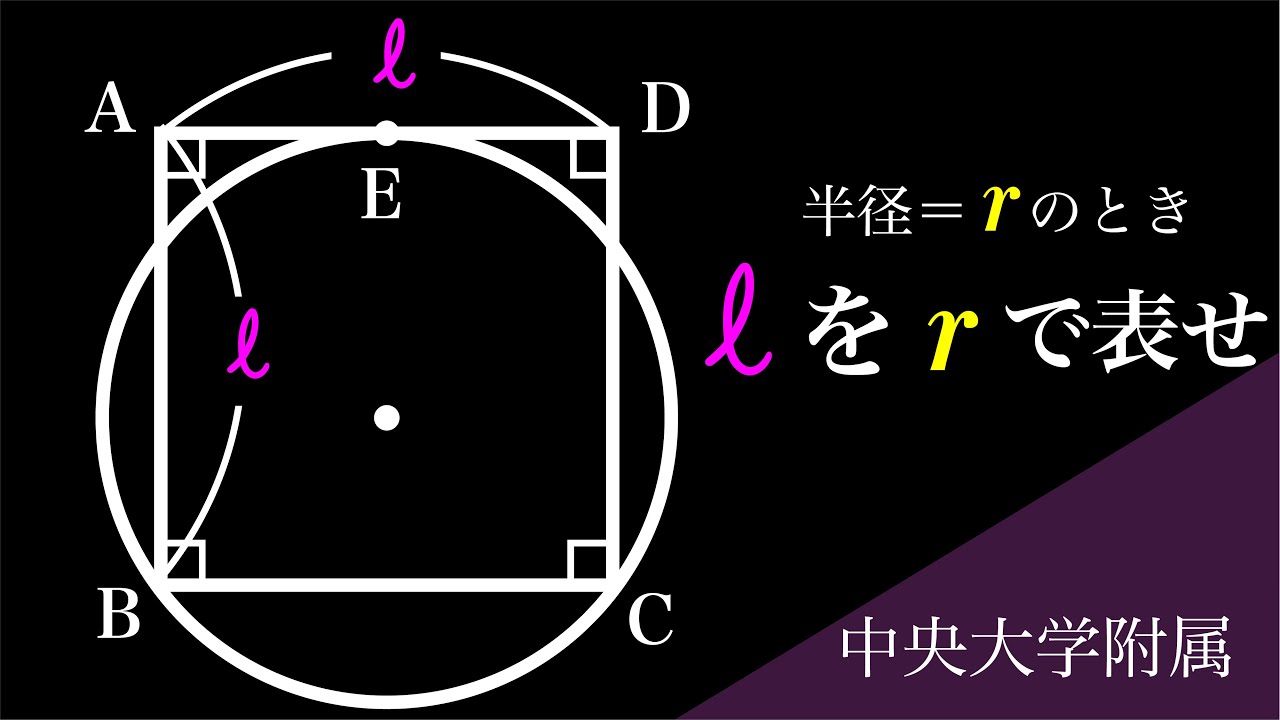
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
この動画を見る
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
中1数学「展開図が正方形の三角錐」【毎日配信】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第63回展開図が正方形の三角錐
例題
ある立体を展開図に表したら、次の図のように 1辺が6cmの正方形になりました。
(1)この立体の表面積は何cmですか。
(2) この立体の体積は何cmですか。
(3) 面AEFを底面としたときの高さは、 何cmですか。
この動画を見る
中1~第63回展開図が正方形の三角錐
例題
ある立体を展開図に表したら、次の図のように 1辺が6cmの正方形になりました。
(1)この立体の表面積は何cmですか。
(2) この立体の体積は何cmですか。
(3) 面AEFを底面としたときの高さは、 何cmですか。
補助線のセンス問われます 円と三平方の定理 中央大附属

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校
この動画を見る
半径=2
BH=?
*図は動画内参照
中央大学附属高等学校
整数問題 大阪星光学院

単元:
#計算と数の性質#数の性質その他#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2b^2=a^2c^2+27$を満たす自然数a,b,cの組をすべて求めよ。
大阪星光学院高等学校
この動画を見る
$a^2b^2=a^2c^2+27$を満たす自然数a,b,cの組をすべて求めよ。
大阪星光学院高等学校
因数分解:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
この動画を見る
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
【高校受験対策/数学】死守62

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
確率:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
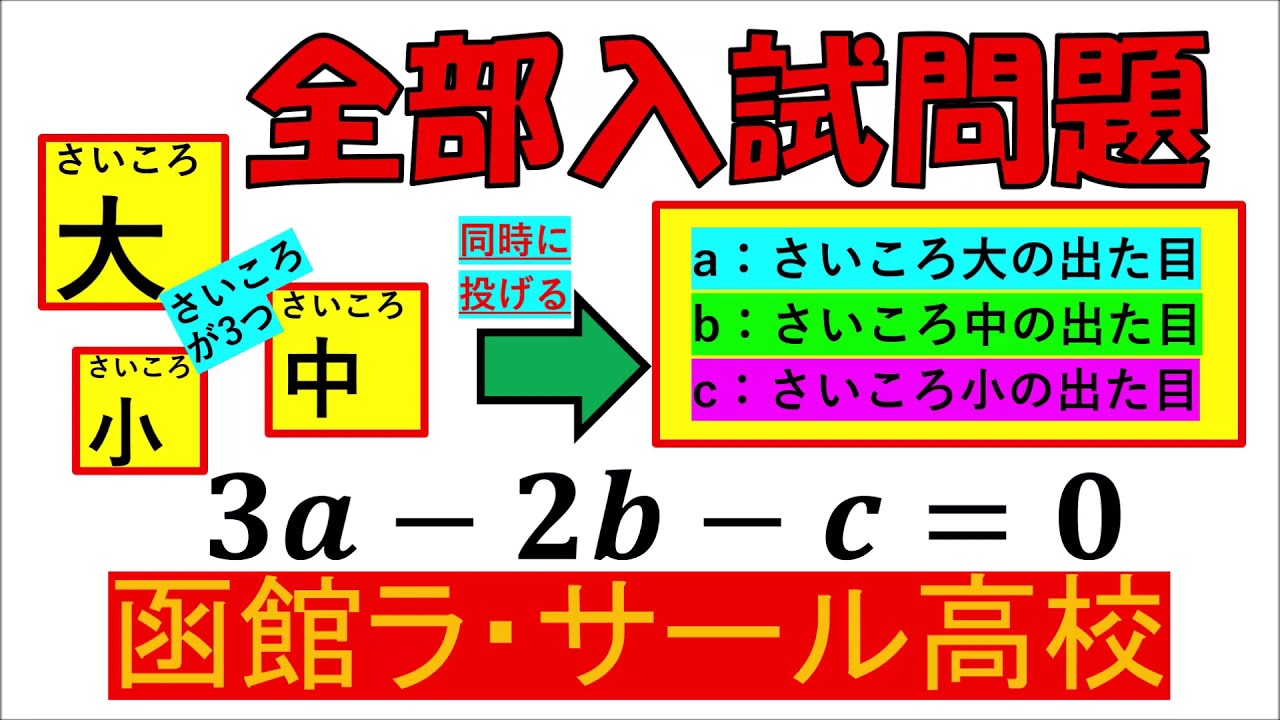
入試問題 函館ラ・サール高等学校
サイズが異なるさいころを同時に投げ、
a: さいころ大の出た目
b: さいころ中の出た目
c: さいころ小の出た目
$3а - 2b - c = 0$
となる確率を求めなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
サイズが異なるさいころを同時に投げ、
a: さいころ大の出た目
b: さいころ中の出た目
c: さいころ小の出た目
$3а - 2b - c = 0$
となる確率を求めなさい。
【中学数学】作図の演習~大分県公立高校過去問2019年~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#大分県公立高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【大分県公立高校過去問2019年】作図の演習
この動画を見る
【大分県公立高校過去問2019年】作図の演習
2001を素因数分解せよ 土佐高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
この動画を見る
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
三平方の定理?いやいや〇〇でしょ A
単元:
#数学(中学生)#中2数学#中3数学#三平方の定理#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
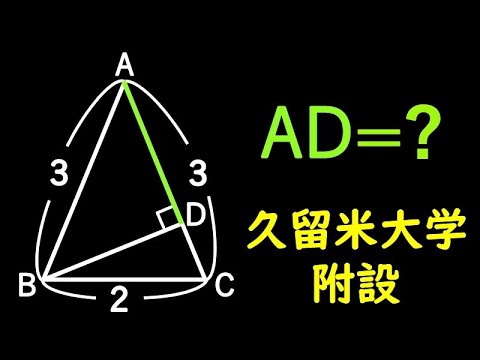
AD=?
*図は動画内参照
久留米大学附設高等学校
この動画を見る
AD=?
*図は動画内参照
久留米大学附設高等学校
因数分解:函館ラ・サール高等学校~全国入試問題解法【メリクリ!】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
中1数学「直線と平面の位置関係」【毎日配信】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~直線と平面の位置関係~
例題 次の図は正六角柱です。
(1) 辺AGと平行な面は何面 ありますか。
(2)辺AGと垂直な面は何面 ありますか。
(3) 面ABCDEFと平行な辺は 何本ありますか。
(4)面ABCDEFと垂直な辺は 何本ありますか。
この動画を見る
中1~直線と平面の位置関係~
例題 次の図は正六角柱です。
(1) 辺AGと平行な面は何面 ありますか。
(2)辺AGと垂直な面は何面 ありますか。
(3) 面ABCDEFと平行な辺は 何本ありますか。
(4)面ABCDEFと垂直な辺は 何本ありますか。
整数:函館ラ・サール高等学校~全国入試問題解法【メリクリ!】

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$N=2020-\sqrt{ 218x }$
N:整数, x:自然数
Nの絶対値の最小値を求めなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
$N=2020-\sqrt{ 218x }$
N:整数, x:自然数
Nの絶対値の最小値を求めなさい。
【中学数学】作図の仕方のまとめ~コンパスと定規を使う問題~

互いに素の個数と和 慶應志木

単元:
#計算と数の性質#数の性質その他#数学(中学生)#文章題#文章題その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1から123までの自然数のうち123と互いに素であるものの個数とその総和を求めよ。
慶應義塾志木高等学校
この動画を見る
1から123までの自然数のうち123と互いに素であるものの個数とその総和を求めよ。
慶應義塾志木高等学校
【中学数学】関数y=ax²:y=1/2x²とy=ax+bが2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき (1)点Aの座標 (2)直線ABの式 (3)△OABの面積 を求めよ。
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
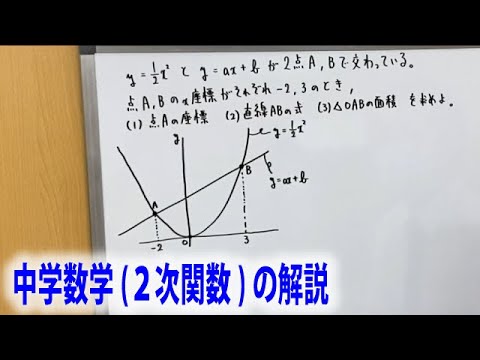
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
この動画を見る
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
中1数学「2直線の位置関係(ねじれ)」【毎日配信】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第61回2直線の位置関係~
例題 次の図は正六角柱です。
(1) 辺ABと平行な辺は何本ですか。
(2) 辺ABと垂直な辺は何本ですか。
(3) 辺ABとねじれの位置は何本ですか。
この動画を見る
中1~第61回2直線の位置関係~
例題 次の図は正六角柱です。
(1) 辺ABと平行な辺は何本ですか。
(2) 辺ABと垂直な辺は何本ですか。
(3) 辺ABとねじれの位置は何本ですか。
反比例と2次方程式 B
単元:
#数学(中学生)#中1数学#中3数学#2次方程式#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
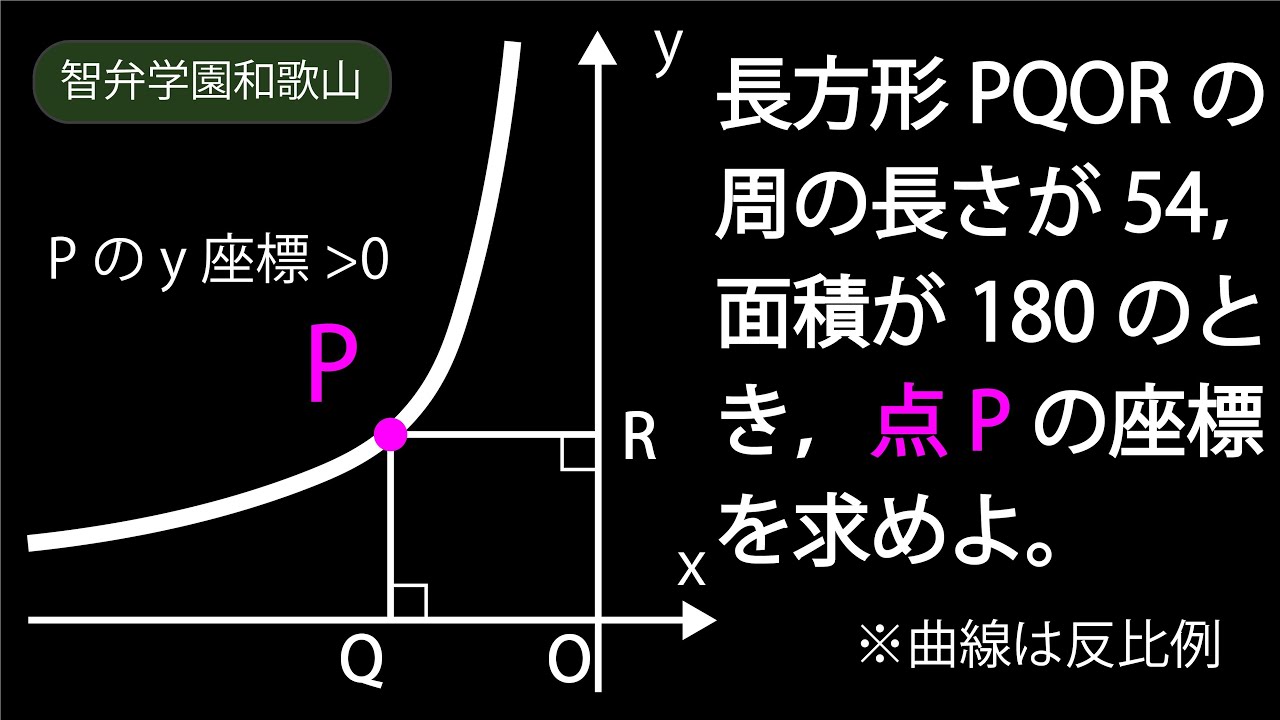
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
この動画を見る
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
平方根:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
この動画を見る
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
