数学検定・数学甲子園・数学オリンピック等
数学検定・数学甲子園・数学オリンピック等
練習問題47 東京理科大学 部分積分 数検準1級 教員採用試験
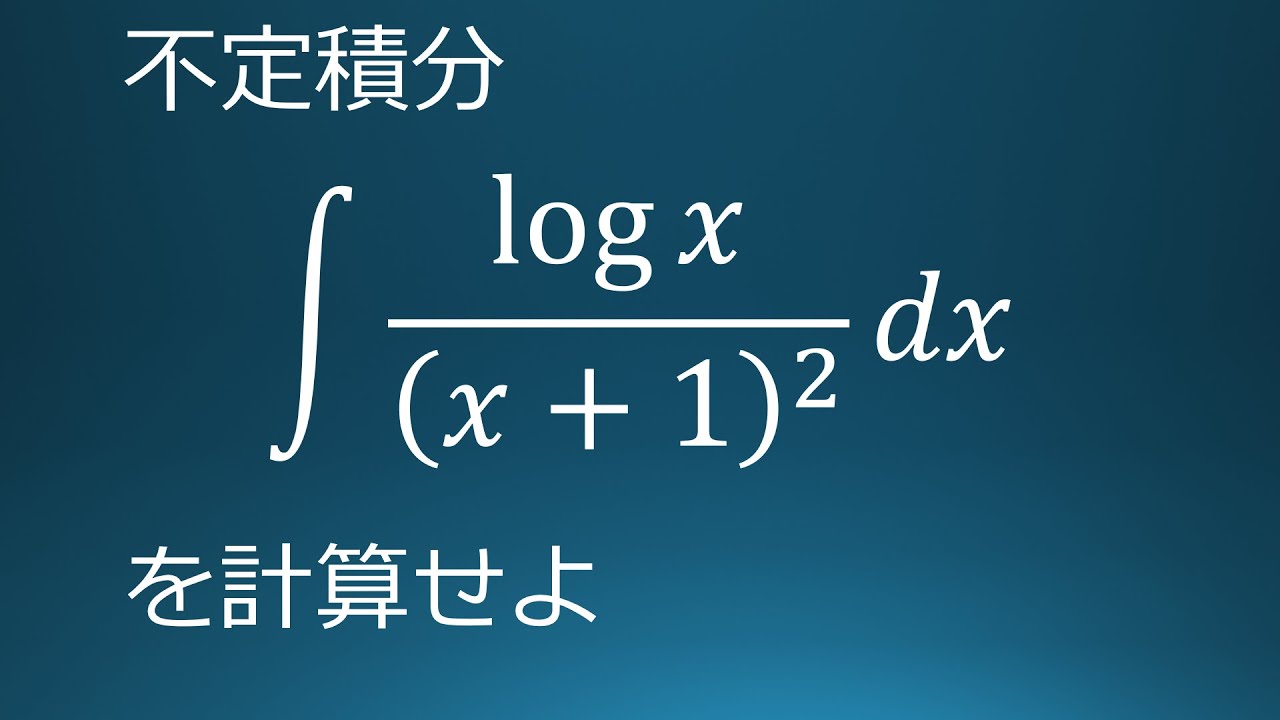
単元：
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#東京理科大学#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{log\ x}{(x+1)^2}\ dx$を計算せよ。
出典：東京理科大学
この動画を見る
$\displaystyle \int \displaystyle \frac{log\ x}{(x+1)^2}\ dx$を計算せよ。
出典：東京理科大学
練習問題46 岡山大学 対数の性質を利用した不等式の証明 数検準１級 教員採用試験
単元：
#数Ⅱ#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#指数関数と対数関数#対数関数#微分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#岡山大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
この動画を見る
実数$a,b,$は
$0 \lt a \lt b$をみたしているとき
$(b+1)^a \lt (a+1)^b$が成り立つことを表せ。
出典：岡山大学
練習問題45 北海道大学 微分と積分 教員採用試験 数検準1級
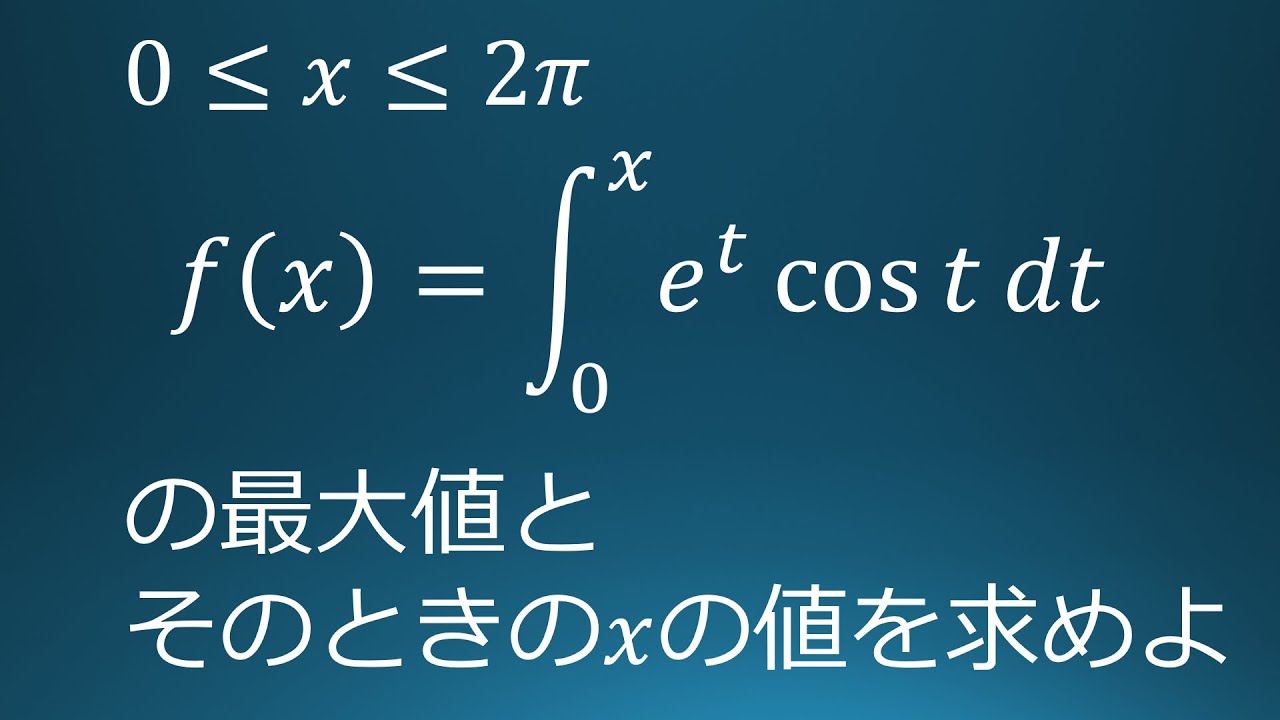
単元：
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#微分とその応用#積分とその応用#学校別大学入試過去問解説(数学)#その他#数学検定#数学検定準1級#数学(高校生)#北海道大学#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
この動画を見る
$0 \leqq x \leqq 2\pi$
関数
$f(x)=\displaystyle \int_{0}^{x}e^t\ cos\ t\ dt$の最大値とそのときの$x$の値を求めよ。
出典：北海道大学 教員採用試験
練習問題44 東京工業大学 極限値 数検1級 教員採用試験（数学）
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題
練習問題43 区分求積法 数検１級１次 教員採用試験
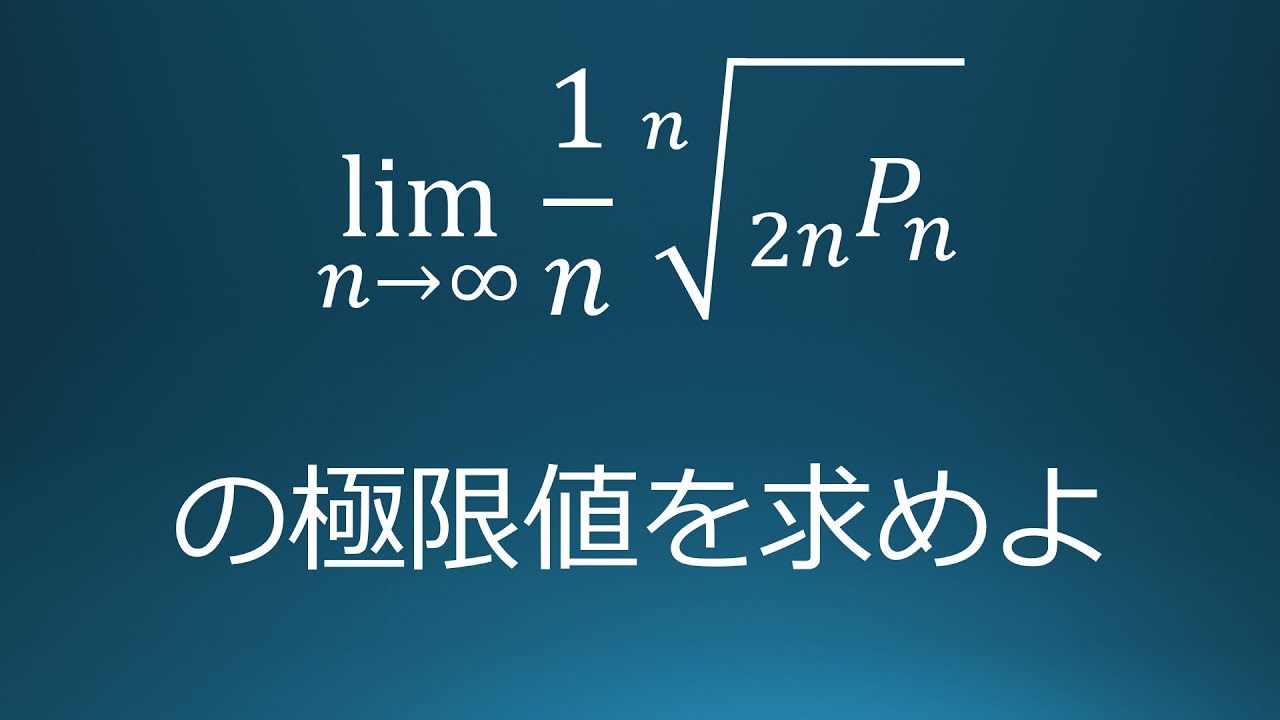
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
練習問題41 微分方程式（数研1級1次 高専数学 教員採用試験）
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.
練習問題40 数研1級1次 高専数学 教採対応 微分方程式
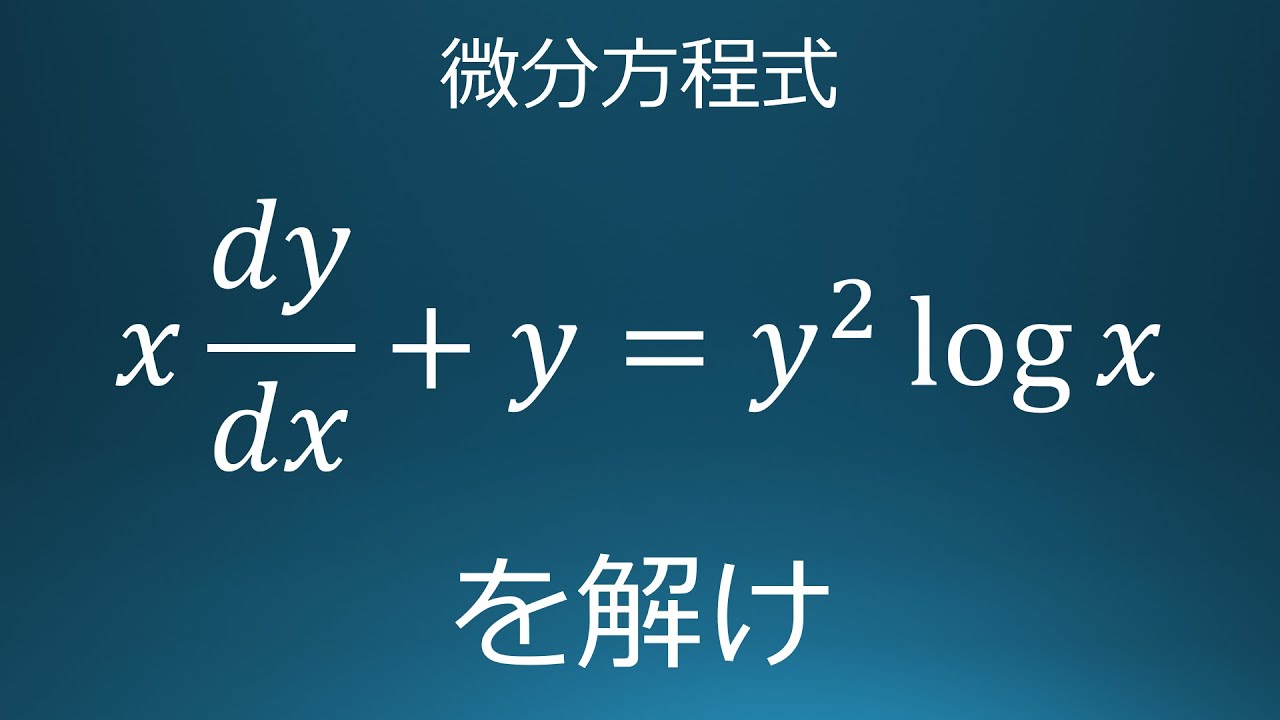
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$x\dfrac{dy}{dx}+y=y^2\log x$の
一般解を求めよ.
この動画を見る
$x\dfrac{dy}{dx}+y=y^2\log x$の
一般解を求めよ.
【数学】高校生でもわかる写像の考え方
単元：
#数学検定・数学甲子園・数学オリンピック等#その他#その他#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
高校生でもわかる写像の考え方に関して解説していきます.
この動画を見る
高校生でもわかる写像の考え方に関して解説していきます.
練習問題39 数研1級1次 教採対応 定積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\dfrac{x+3}{x^2-2x+2}dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{0}^{1}\dfrac{x+3}{x^2-2x+2}dx$
を計算せよ.
練習問題38 数検1級1次 高専数学 積分順序の変更
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
$\displaystyle \int_{0}^{a} dx \displaystyle \int_{0}^{x^2} f(x,y)dy$
の積分順序の変更をせよ.
この動画を見る
$a\gt 0$とする.
$\displaystyle \int_{0}^{a} dx \displaystyle \int_{0}^{x^2} f(x,y)dy$
の積分順序の変更をせよ.
練習問題37 数検1級1次 高専数学 教採 重積分の積分順序の変更
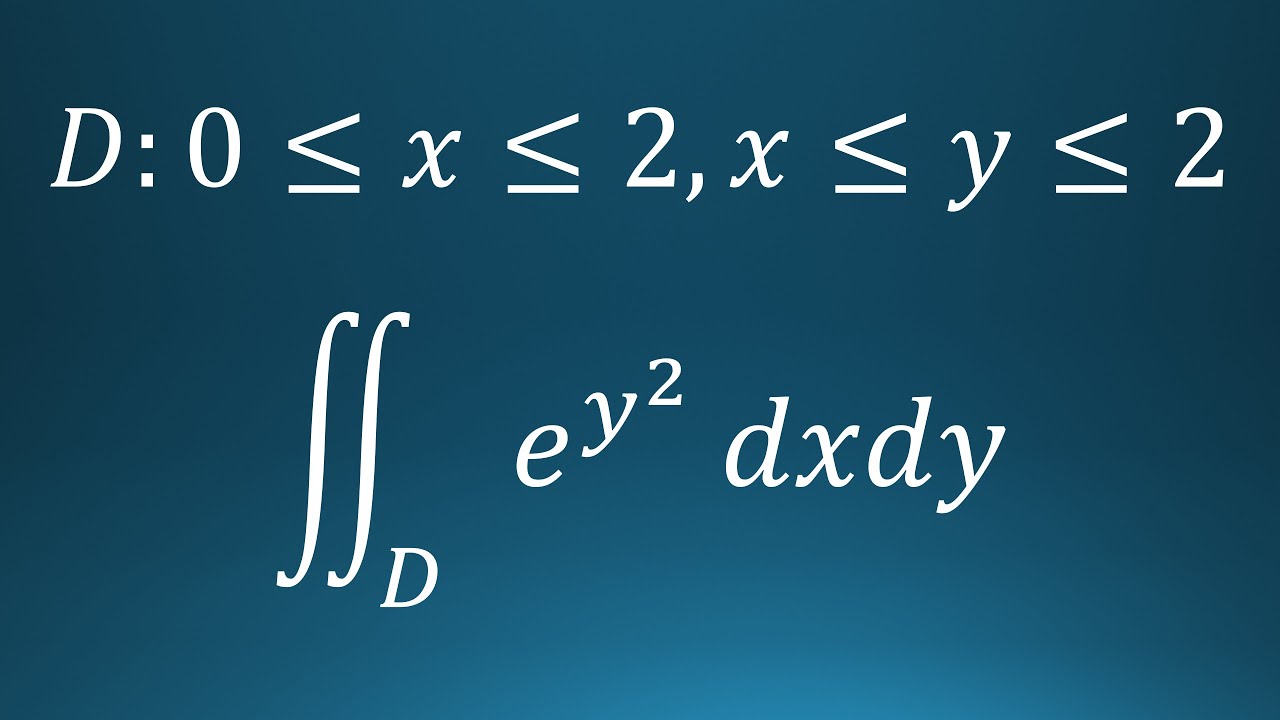
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$D:0\leqq x \leqq 2,x \leqq y \leqq 2$
$ \displaystyle \iint_D e^{y^2} dx \ dy$を計算せよ.
この動画を見る
$D:0\leqq x \leqq 2,x \leqq y \leqq 2$
$ \displaystyle \iint_D e^{y^2} dx \ dy$を計算せよ.
【裏技】なんの2乗か一瞬で出せる方法～学校では教えてくれない～
単元：
#算数(中学受験)#数学検定・数学甲子園・数学オリンピック等#その他#その他#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1849は43²
2乗の数をすぐに出せる裏技紹介！
この動画を見る
1849は43²
2乗の数をすぐに出せる裏技紹介！
練習問題36 （数検1級1次 教採 極限値）
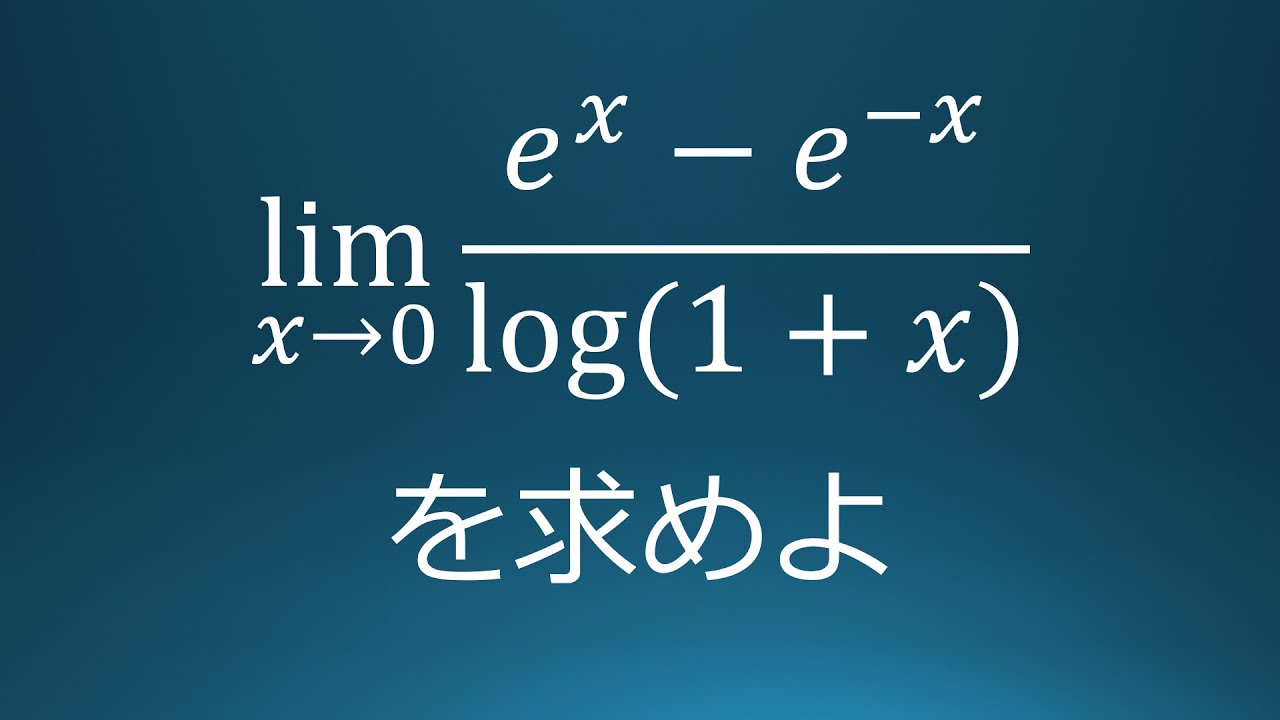
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{e^x-e^{-x}}{\log (1+x)}$
を求めよ.
計算が速くなるテクニック～5を使いこなせ～
単元：
#算数(中学受験)#数学検定・数学甲子園・数学オリンピック等#その他#その他#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
73×5
184×25
120×125
3秒で解ける計算テクニックを紹介！
この動画を見る
73×5
184×25
120×125
3秒で解ける計算テクニックを紹介！
練習問題35 数学オリンピックの問題 複素数を利用して証明してみた。
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学オリンピック#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
【計算が速くなる方法】2桁の掛け算のテクニック～日本初！？～
単元：
#算数(中学受験)#数学検定・数学甲子園・数学オリンピック等#その他#その他#その他#その他#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
71×62=
23×41=
2桁のかけ算が一瞬で解ける方法を教えます！
この動画を見る
71×62=
23×41=
2桁のかけ算が一瞬で解ける方法を教えます！
練習問題34 数検1級1次 微分方程式
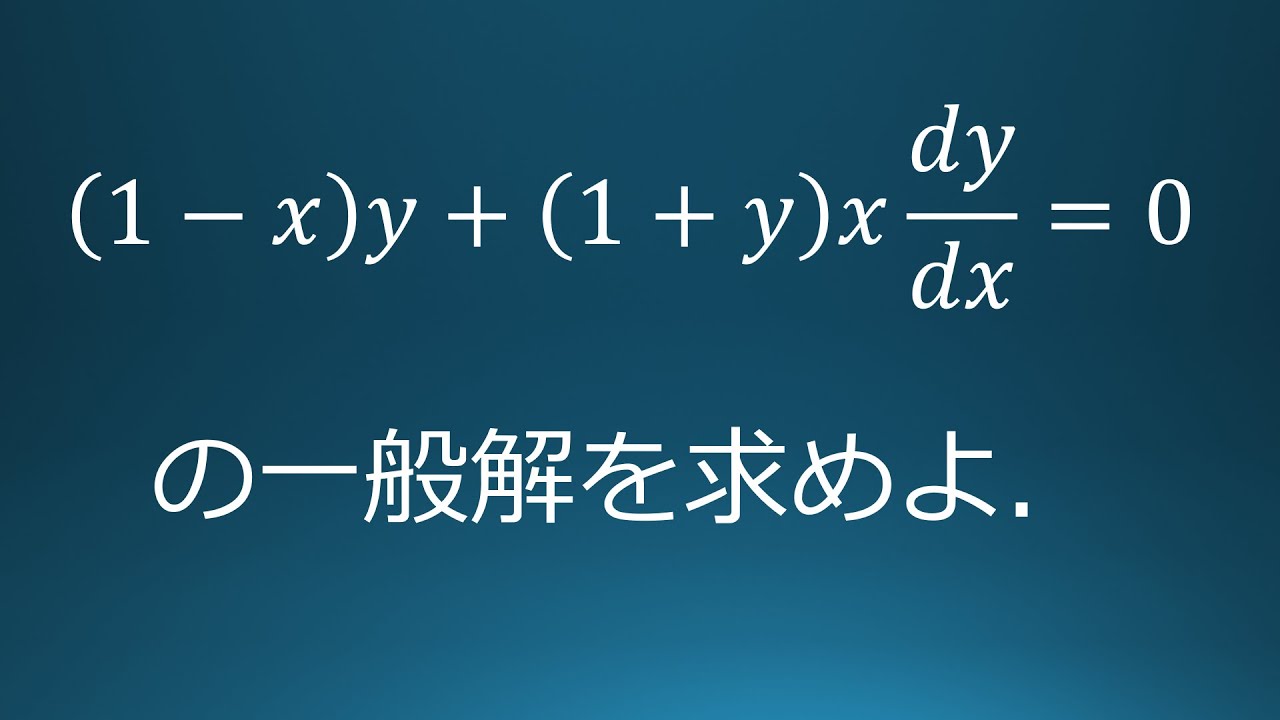
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
練習問題33 数検1級1次 微分方程式
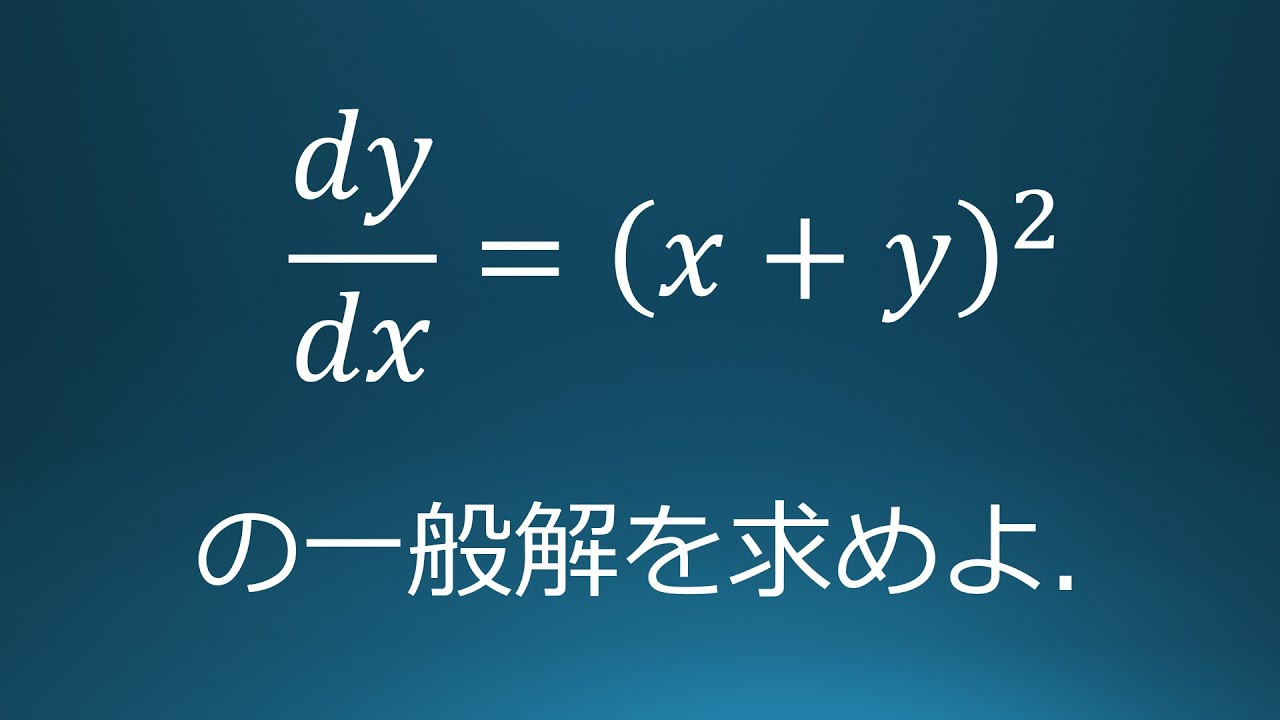
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
この動画を見る
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.
2通りの解説 ジュニア数学オリンピック B
#20 数検1級1次過去問 3重積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$
$\iiint_D x^3y^2z \ dx \ dy \ dz$
$D:0\leq x\leq y\leq z\leq 1$
を求めよ.
この動画を見る
$\boxed{7}$
$\iiint_D x^3y^2z \ dx \ dy \ dz$
$D:0\leq x\leq y\leq z\leq 1$
を求めよ.
練習問題31 積分 数検準1級 教採対応
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#その他#数学検定#数学検定準1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \dfrac{\tan^{-1}x+1}{x^2+1}dx$
を計算せよ.
この動画を見る
$\displaystyle \int_{0}^{1} \dfrac{\tan^{-1}x+1}{x^2+1}dx$
を計算せよ.
練習問題30 積分（ｙ軸回転体） 数検 教採
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#その他#不定積分・定積分#数学検定#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$y=\log(x+1),y=3$
$y$軸で囲まれた部分を$y$軸を中心として
回転したときの体積$V$を求めよ.
この動画を見る
$y=\log(x+1),y=3$
$y$軸で囲まれた部分を$y$軸を中心として
回転したときの体積$V$を求めよ.
#19数検準1級 極限値（はさみうちの原理）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \displaystyle \int_{0}^{1} \dfrac{x^n}{1+x^2} dx$
を求めよ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \int_{0}^{1} \dfrac{x^n}{1+x^2} dx$
を求めよ.
#18数検1級1次過去問 3重積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
この動画を見る
$\boxed{7}$
$D:x^2+y^2 \leqq z \leqq 2x$
$ \displaystyle \iiint_D \ dx\ dy\ dz$
の値を求めよ.
微分方程式（同次型） p 163, q3(1) 高専数学 数検1級
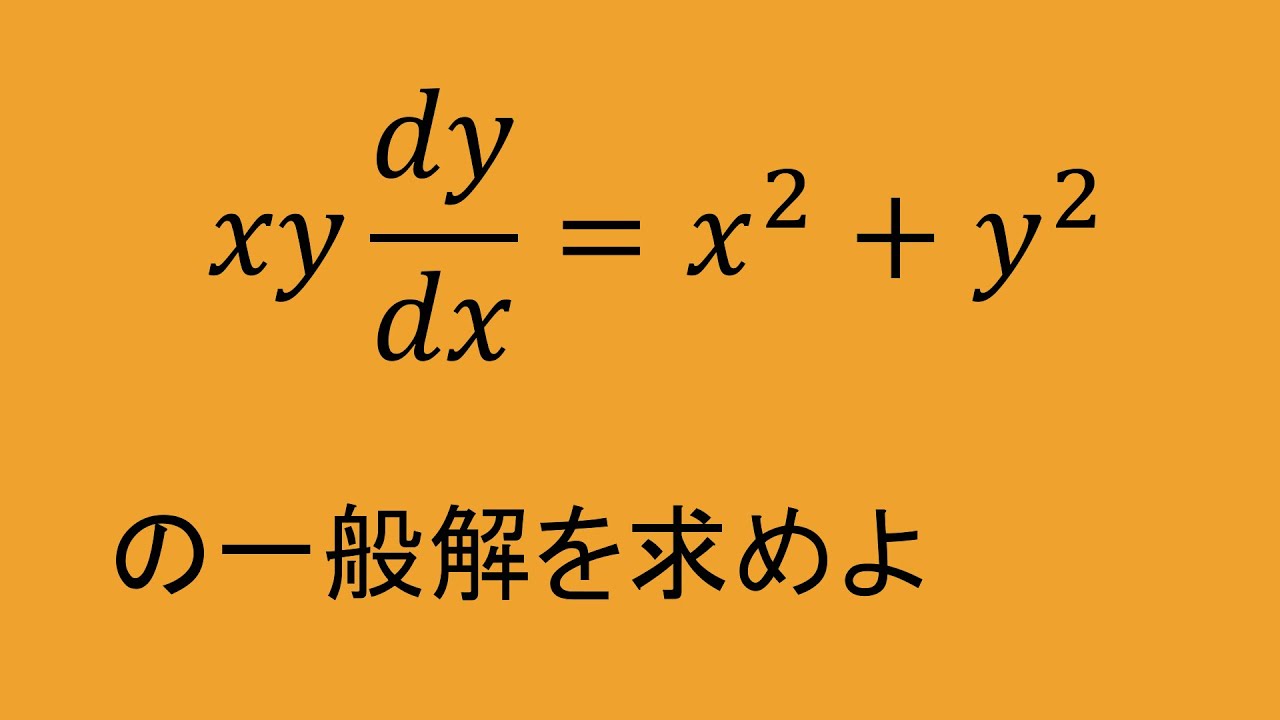
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$xy\dfrac{dy}{dx}=x^2+y^2$の一般項を求めよ.
この動画を見る
$xy\dfrac{dy}{dx}=x^2+y^2$の一般項を求めよ.
#17数検1級1次 過去問 微分
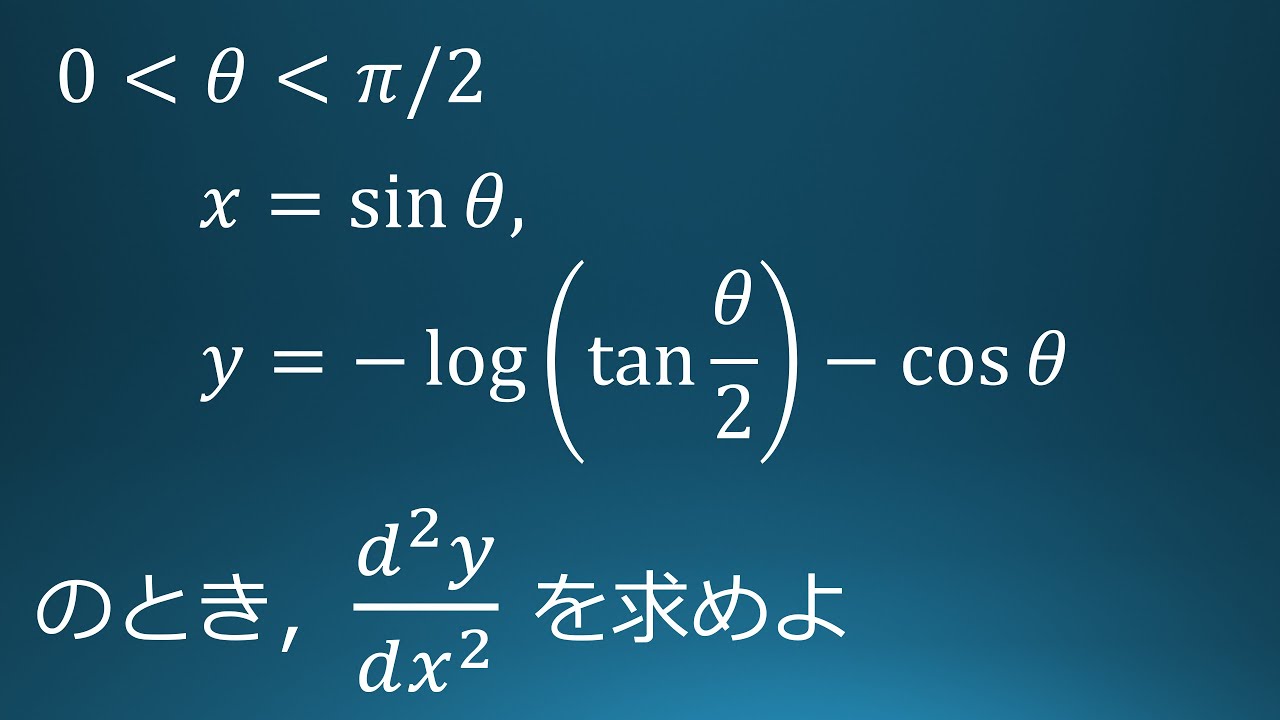
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#微分法#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$0\lt \theta\lt \dfrac{\pi}{2}$,
$x=\sin\theta$
$y=-\log\left(\tan\dfrac{\theta}{2}\right)-\cos\theta$とする.
$\dfrac{d^2y}{dx^2}$を$\theta$で表せ.
この動画を見る
$\boxed{6}$
$0\lt \theta\lt \dfrac{\pi}{2}$,
$x=\sin\theta$
$y=-\log\left(\tan\dfrac{\theta}{2}\right)-\cos\theta$とする.
$\dfrac{d^2y}{dx^2}$を$\theta$で表せ.
#16 数検1級1次過去問 複素関数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$i^2=-1$とする.
$\cos(6i)-i\sin(6i)$を求めよ.
この動画を見る
$\boxed{2}$
$i^2=-1$とする.
$\cos(6i)-i\sin(6i)$を求めよ.
練習問題28 極限値 数検 教採対応（防衛大学）
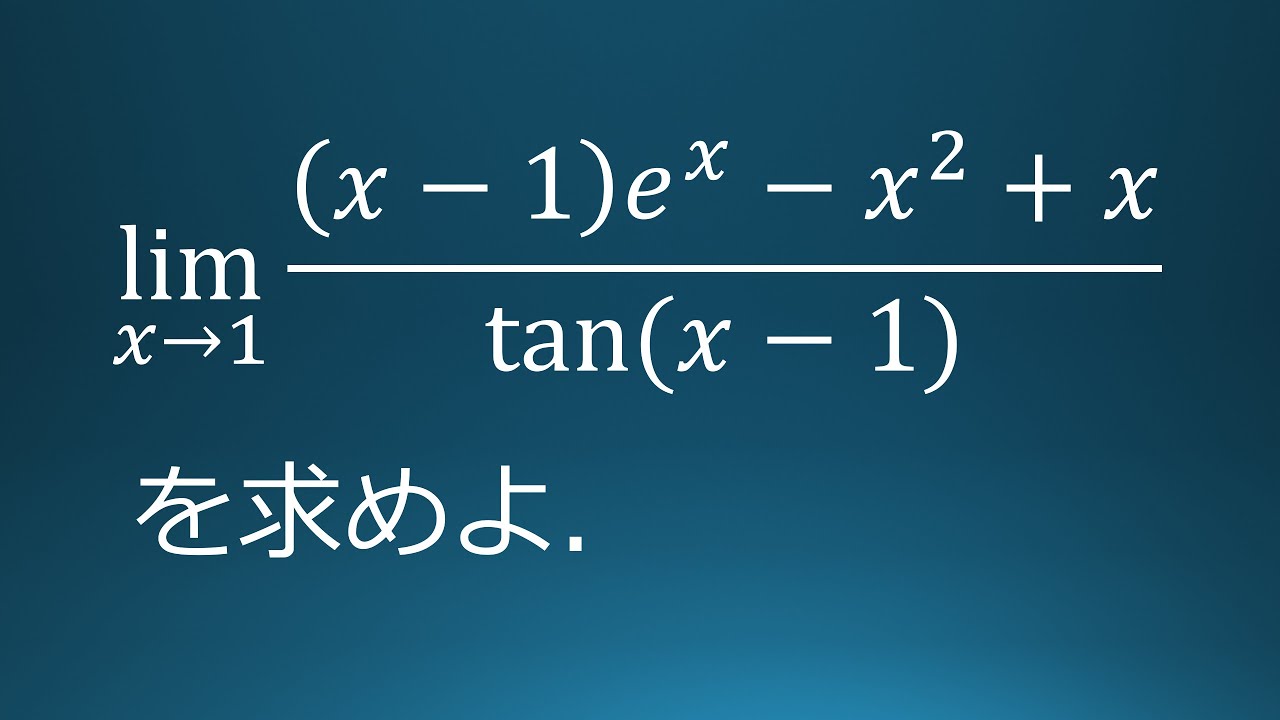
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to 1}\dfrac{(x-1)e^x-x^2+x}{\tan(x-1)}$を求めよ.
この動画を見る
$\displaystyle \lim_{x\to 1}\dfrac{(x-1)e^x-x^2+x}{\tan(x-1)}$を求めよ.
#1微分方程式練習問題 （高専数学 数検1級）
単元：
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$ x\dfrac{dy}{dx}=y(\log y-\log x+1)$
の一般解を求めよ.
この動画を見る
$ x\dfrac{dy}{dx}=y(\log y-\log x+1)$
の一般解を求めよ.
#15 数検1級1次 過去問 3重積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.
$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.
この動画を見る
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.
$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.