福田のおもしろ数学054〜不等式の再利用のコツ〜2つの不等式の証明

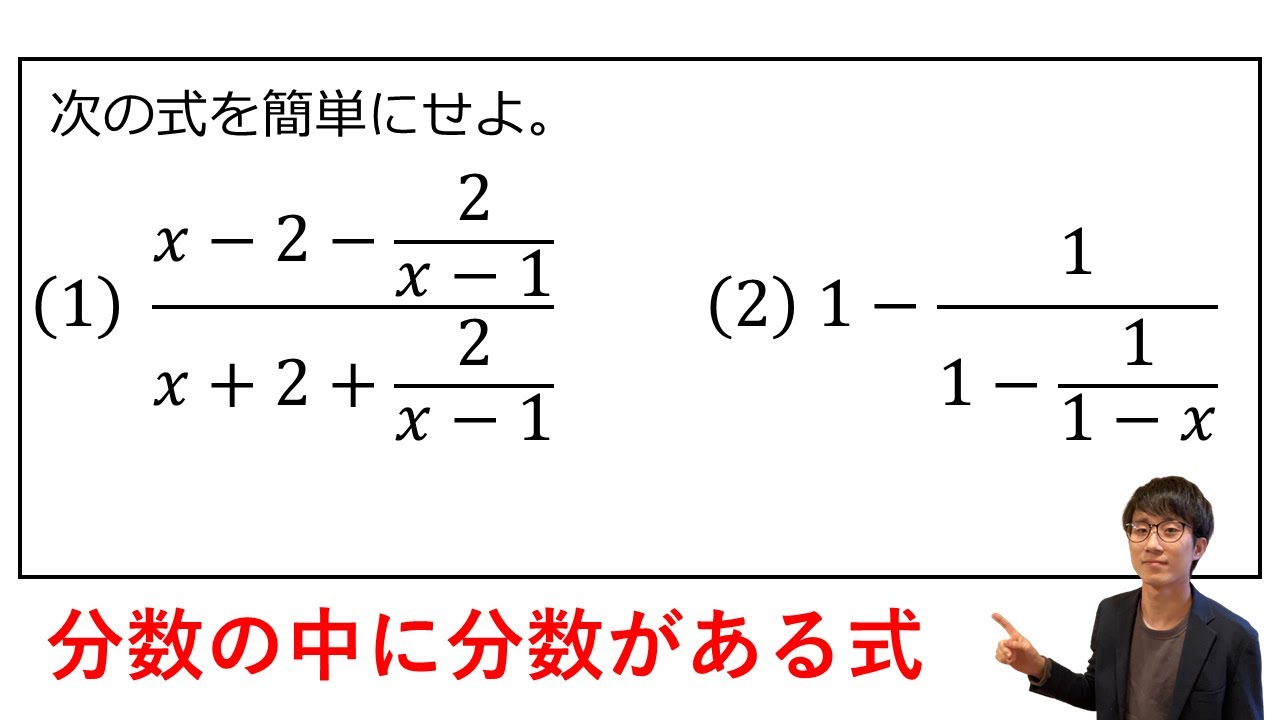
問題文全文(内容文)：
前段の不等式をいかに利用するか？
$a^2+b^2+c^2 \geqq ab+bc+ca$
$a^4+b^4+c^4 \geqq abc(a+b+c)$
を証明せよ！

単元： #数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
前段の不等式をいかに利用するか？
$a^2+b^2+c^2 \geqq ab+bc+ca$
$a^4+b^4+c^4 \geqq abc(a+b+c)$
を証明せよ！

投稿日：2024.02.17

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#恒等式・等式・不等式の証明#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学#数C

指導講師：鈴木貫太郎

問題文全文(内容文)：
島根大学過去問題
a,b,c実数
$a+b+c=3$
$ab+bc+ca \leqq 3$を示せ。

愛知工業大学過去問題
$Z=1-i$
$Z^7+Z^6+Z^5+Z^4+Z^3+Z^2+Z+1$の値

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#三角関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
2014京都大学過去問題
$0 \leqq θ < 90^\circ \quad$xについての4次方程式
$\{ x^2-2(cosθ)x-cosθ+1 \} x$
$\{ x^2-2(tanθ)x+3 \} = 0$は虚数解を少なくとも1つ持つことを示せ。

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$P_k(x)=1+x+x^2+\cdots +x^{k-1}$のとき、
$\displaystyle \sum^n_{k=1}{} _nC_kP_k(x)=2^{n-1}P_n(\dfrac{1+x}2)$
が成り立つことを証明せよ。

この動画を見る　

単元： #数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+･･･････+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#対数関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
実数の組$(x,y,z)$で、どのような整数$l,m,n$に対しても$l・10^{x-y}-nx+l・10^{y-z}+m・10^{x-z}=$
13l+36m+ny$が成り立つものを求めよ

出典：2011年大阪大学　過去問

この動画を見る　