問題文全文(内容文):
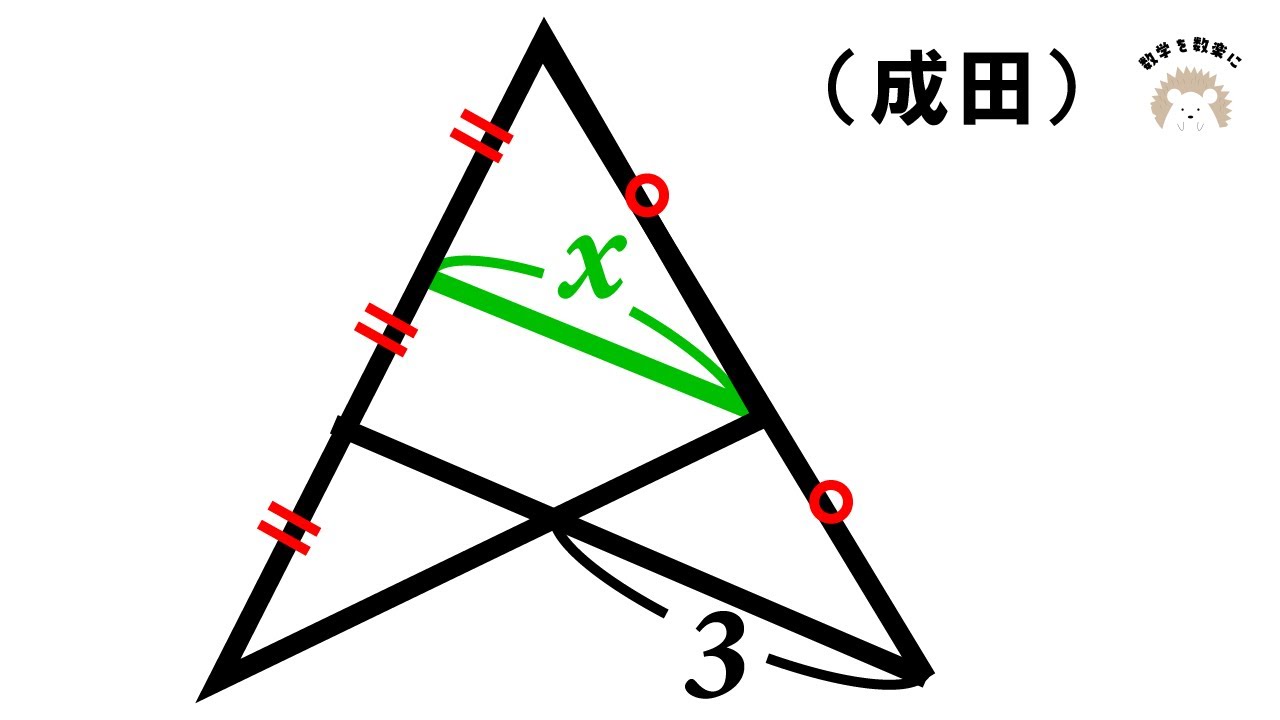
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
チャプター:
00:00 はじまり
00:18 問題だよ
00:32 問題解説(1)
05:40 問題解説(2)
10:47 まとめと感想
11:13 問題と答え
単元:
#数学(中学生)#中3数学#相似な図形#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
投稿日:2021.01.06