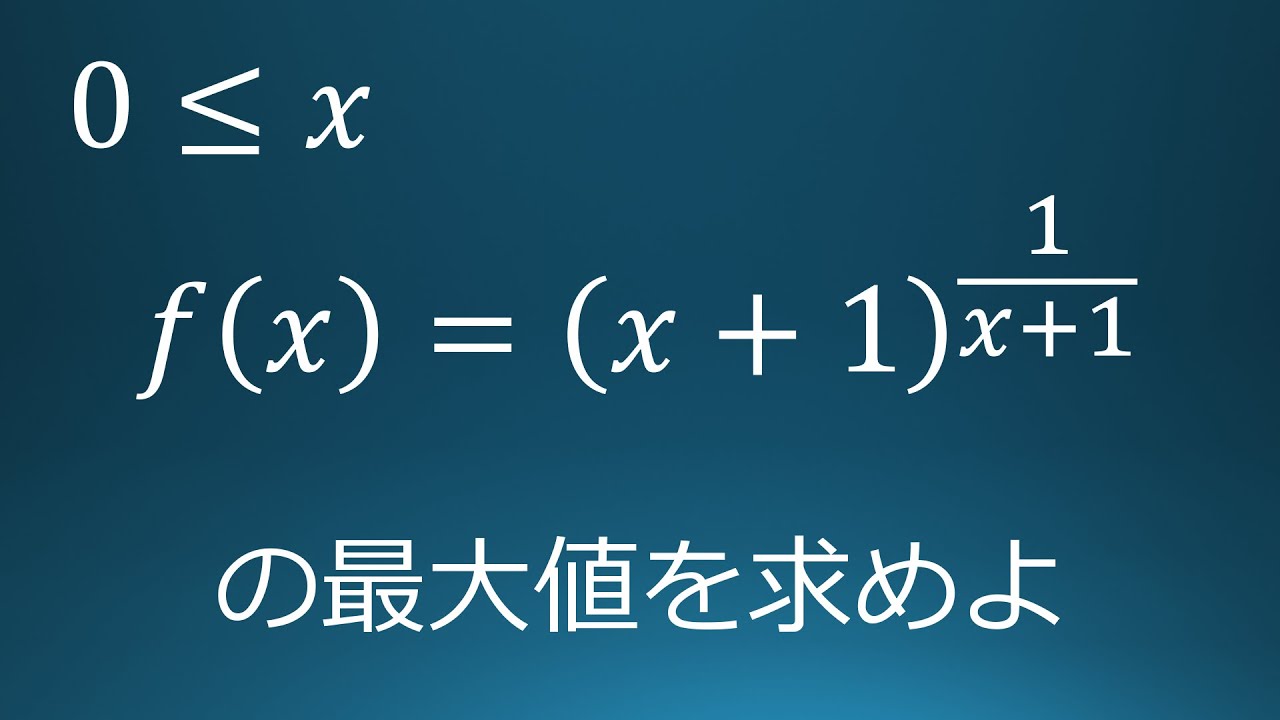問題文全文(内容文):
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
投稿日:2024.08.04