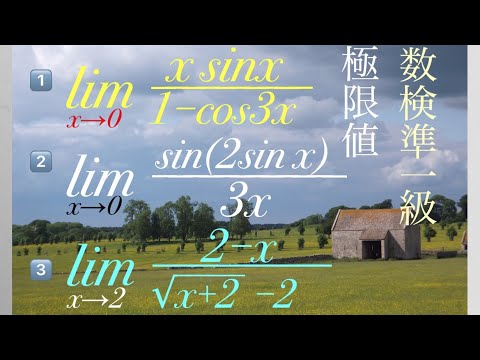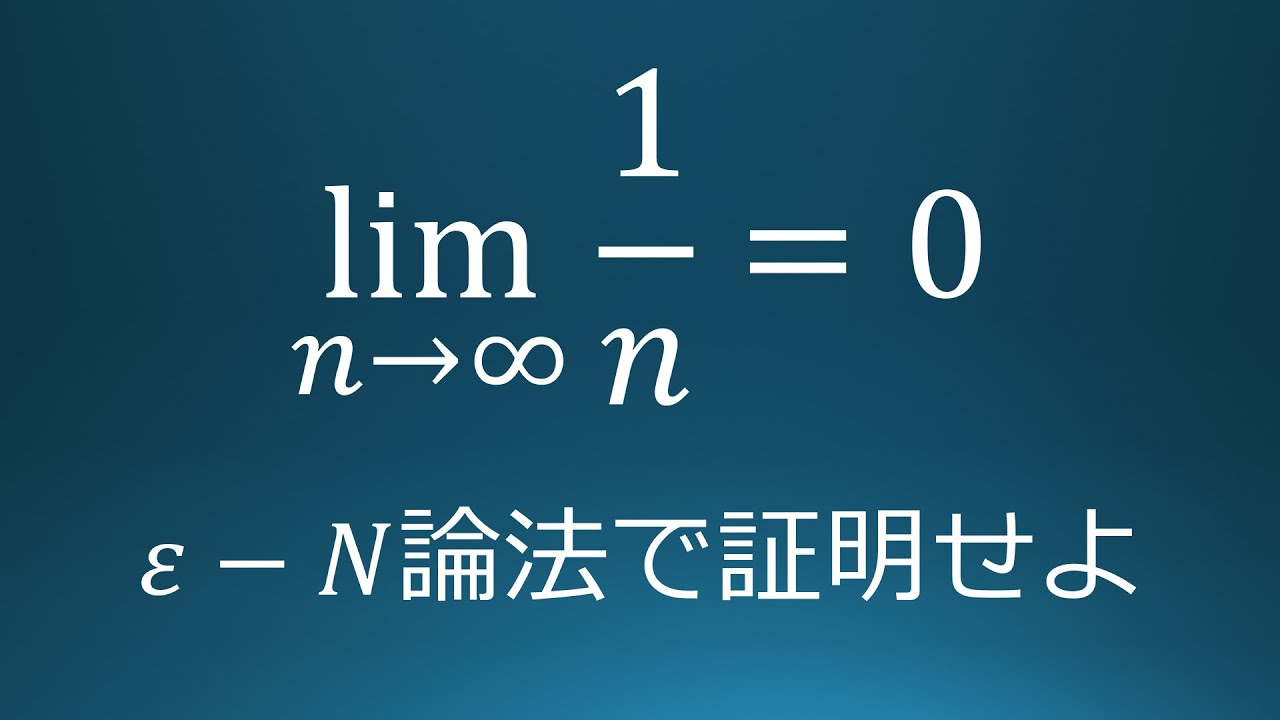極限 - 質問解決D.B.（データベース）

単元： #微分法と積分法#平均変化率・極限・導関数

指導講師：数学を数楽に

投稿日：2024.07.31

単元： #数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎次の条件を満たす3次関数$f(x)$を求めよう。

①$x^3$の係数が$1,f(1)=2, f(-1)=-2, f'(-1)=0$

② $f(x) +x f(x) = 4x^3-9x^2+6x+1$

この動画を見る　

単元： #数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
限値からの区分求積法を解説していきます.

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.

2022産業医科大学過去問題

この動画を見る　

単元： #数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：

$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
　　　　　

この動画を見る　

単元： #数Ⅱ#微分法と積分法#平均変化率・極限・導関数#微分とその応用#接線と法線・平均値の定理#その他#数学(高校生)#数Ⅲ#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$\boxed{6}-(2)$
$\displaystyle \lim_{x\to 0}\dfrac{\sin (sin x)-\sin x}{\sin x-x}$の
極限値を求めよ.

この動画を見る　