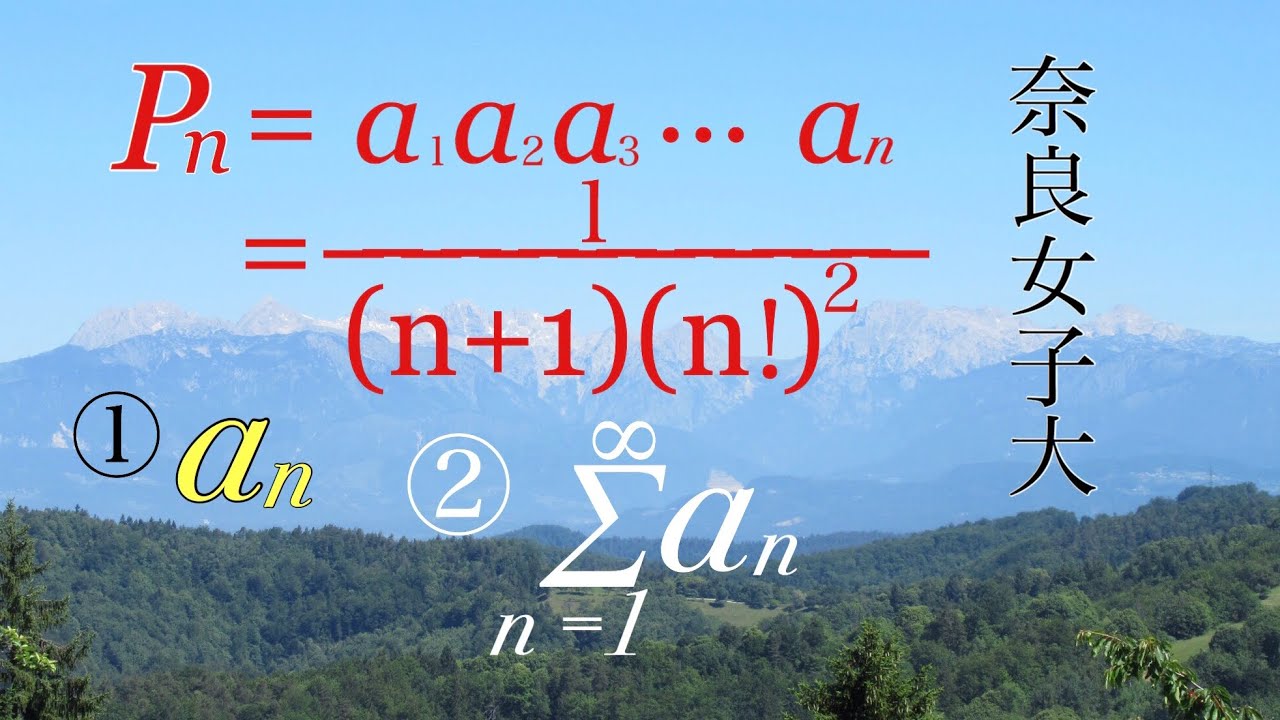問題文全文(内容文):
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
チャプター:
00:00 イントロ(問題紹介)
00:22 本編スタート
09:39 作成した解答①
09:50 作成した解答②
10:00 エンディング
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
$a_1=S$:実数
$(n+2)a_{n+1}=n\ a_n+2$
(1)
$a_n$を求めよ
(2)
$\displaystyle \sum_{n=1}^m a_n=0$のとき$S$を$m$で表せ
出典:2023年東北大学 入試問題
投稿日:2023.04.29