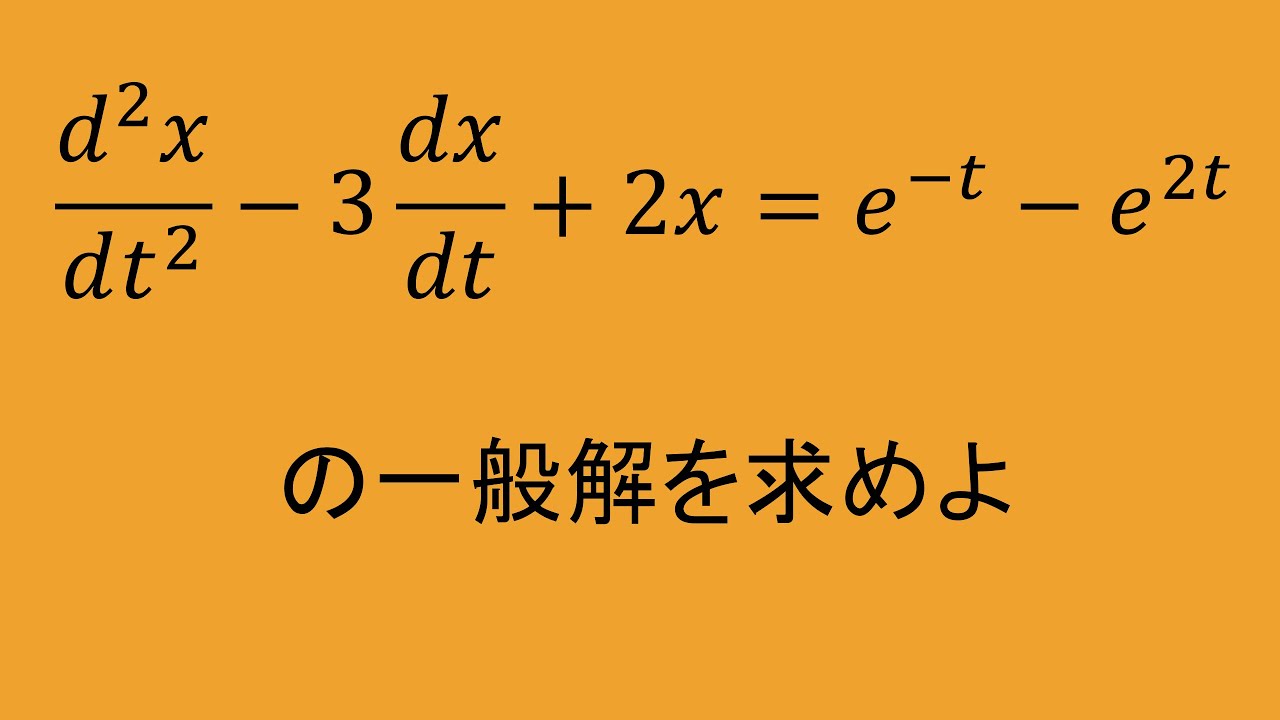問題文全文(内容文):
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
(1)
$\displaystyle \frac{dy}{dx}=\displaystyle \frac{4y}{3x},\ x \gt 0$の一般項を求めよ
(2)
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dy}{dx}=\displaystyle \frac{2y}{3x}+\displaystyle \frac{2x}{y},\ x \gt 0 \\
y(1)=3
\end{array}
\right.
\end{eqnarray}$を満たす解を求めよ
出典:岡山大学大学院 入試問題
投稿日:2023.05.26