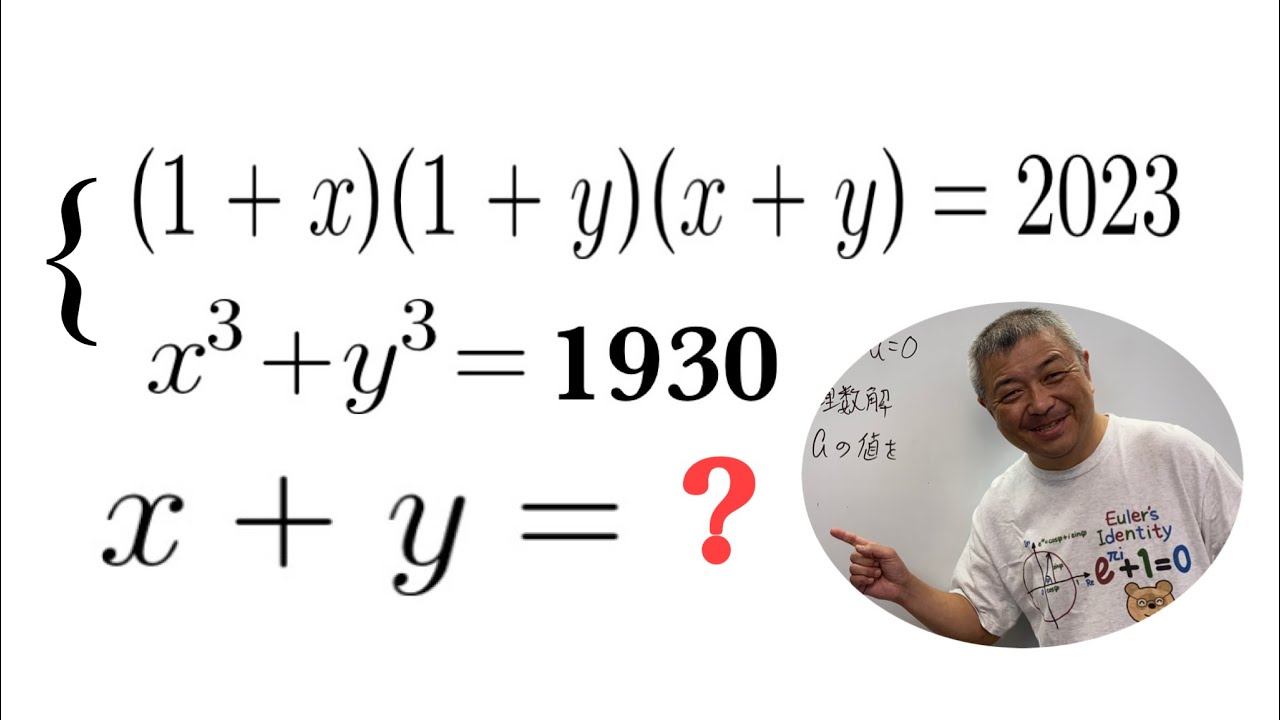奈良県立医大長方形の面積の最大値

問題文全文(内容文)：
動画内の図のような三角形に内接する長方形の面積の最大値を求めよ

出典：奈良県立医科大学　問題

単元： #数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
動画内の図のような三角形に内接する長方形の面積の最大値を求めよ

出典：奈良県立医科大学　問題

投稿日：2019.08.07

単元： #数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
【高校数学　数学Ⅰ　二次関数】
$y=x^2+mx+2$が次の条件を満たすように、定数$m$の値の範囲を定めよ。
(1)このグラフとx軸の正の部分が異なる2点で交わる。
(2)グラフとx軸のx＜-1の部分が異なる2点で交わる。

この動画を見る　

単元： #図形と計量#平面図形#数学(高校生)

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ

この動画を見る　

単元： #数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
整数x,yについて、$97x+83y=23$を満たす整数解x,yの一般解を求めよ.

この動画を見る　

単元： #数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$AE \times CH = OH \times BE$を示せ
＊図は動画内参照

2023西高等学校

この動画を見る　

単元： #算数(中学受験)#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#過去問解説(学校別)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
2つの三角形の面積の和=?
＊図は動画内参照

筑波大学附属駒場中学校

この動画を見る　