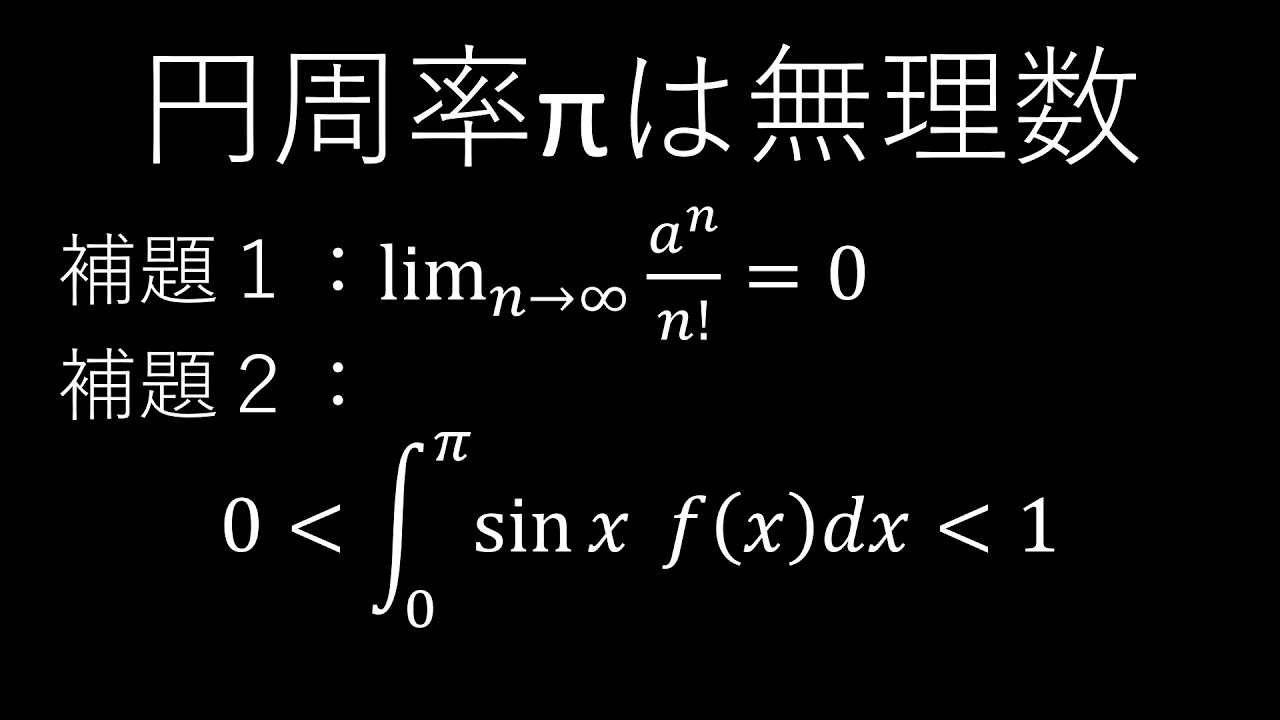#15 数検1級1次過去問 3重積分 - 質問解決D.B.（データベース）

問題文全文(内容文)：
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.

$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.

単元： #数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$V:x^2+y^2+z^2\leqq 4$
$x^2+y^2\leqq 1,z\geqq 0$とする.

$\displaystyle \iiint_V\ z\ dx\ dy \ dz$を求めよ.

投稿日：2021.05.10

単元： #数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
（1）$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7 x$ $dx$

（2）$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^8 x$ $dx$

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int\sqrt{ 2 }$ $logx$ $dx$

出典：2024年　名古屋工業大学

この動画を見る　

単元： #積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ

指導講師：理数個別チャンネル

問題文全文(内容文)：
積分による面積計算の公式③に関して解説していきます.

この動画を見る　

単元： #大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$a \gt 0$
$\displaystyle \int x^2\cos(a\ log\ x)dx$

出典：2012年横浜国立大学　入試問題

この動画を見る　

単元： #大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$

出典：立教大学　入試問題

この動画を見る　