微分でも解けるけど・・・【数学 入試問題】【慶應義塾大学 改題】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅱ > 微分法と積分法 > 微分でも解けるけど・・・【数学 入試問題】【慶應義塾大学 改題】

微分でも解けるけど・・・【数学 入試問題】【慶應義塾大学 改題】

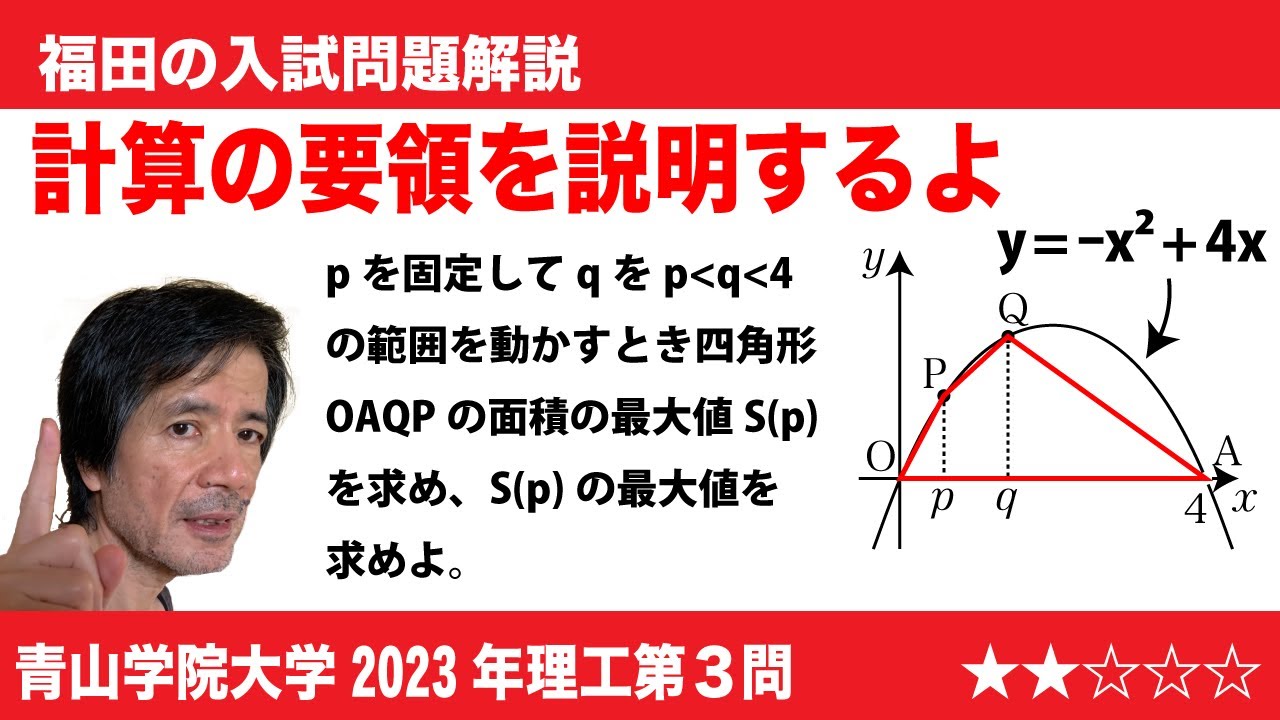
問題文全文(内容文)：
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。

慶應義塾大改題過去問
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師： 数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。

慶應義塾大改題過去問
投稿日：2022.05.20

＜関連動画＞

福田の数学〜九州大学2023年文系第１問〜放物線と直線で囲まれた面積

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師： 福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ aを0＜a＜9 を満たす実数とする。xy平面上の曲線Cと直線lを、次のように定める。
C：$y$=|($x$-3)($x$+3)|,　l：$y$=$a$
曲線Cと直線lで囲まれる図形のうち、$y$≧$a$の領域にある部分の面積を$S_1$、$y$≦$a$の領域にある部分の面積を$S_2$とする。$S_1$=$S_2$となる$a$の値を求めよ。

2023九州大学文系過去問
この動画を見る　

【数学】不等式証明（絶対値ver.）の解法のステップ【1.25倍速再生推奨】

アイキャッチ画像
単元： #数Ⅱ#恒等式・等式・不等式の証明#数学(高校生)
指導講師： カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
【数学】不等式証明（絶対値ver.）の解説動画です
-----------------
$|a-c|\leqq|a-b|+|b-c|$
証明せよ。
この動画を見る　

自治医大　関数の最小値

アイキャッチ画像
単元： #数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#２次関数#式と証明#2次関数とグラフ#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$f(x)=4^x+4^{-x}-2^{x+1}-2^{1-x}$
$f(x)$の最小値とその時の$x$の値を求めよ

出典：自治医科大学　過去問
この動画を見る　

福田の1.5倍速演習〜合格する重要問題045〜東北大学2017年度理系第1問〜絶対値の付いた２次関数のグラフと直線の共有点の個数

アイキャッチ画像
単元： #数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次関数とグラフ#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
$a,b$を実数とする。$y=|x^2-4|$で表される曲線をCとし、
$y=ax+b$で表される直線をlとする。

(1)lが点(-2,0)を通り、lとCがちょうど3つの共有点をもつような
a,bの条件を求めよ。
(2)lとCがちょうど3つの共有点をもつような点(a,b)の軌跡を
ab平面上に図示せよ。

2017東北大学理系過去問
この動画を見る　

東京水産大　三次関数　三角形面積最大 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$f(x)=-x^3+8x+3$
$f(x)$上の2つの定点$A(0,3),B(3,0)$と動点$P(a,f(a))(0 \lt a \lt 3)\triangle PAB$の面積の最大値は？

出典：2002年東京海洋大学　過去問
この動画を見る　
PAGE TOP