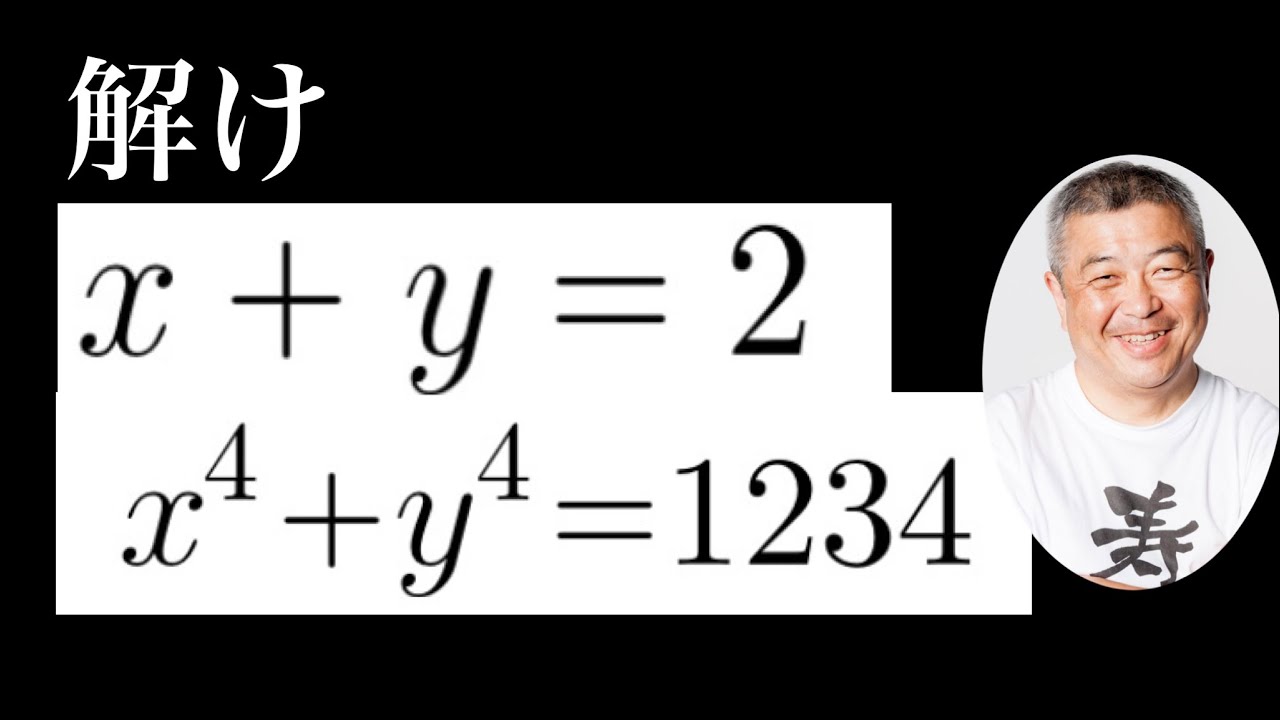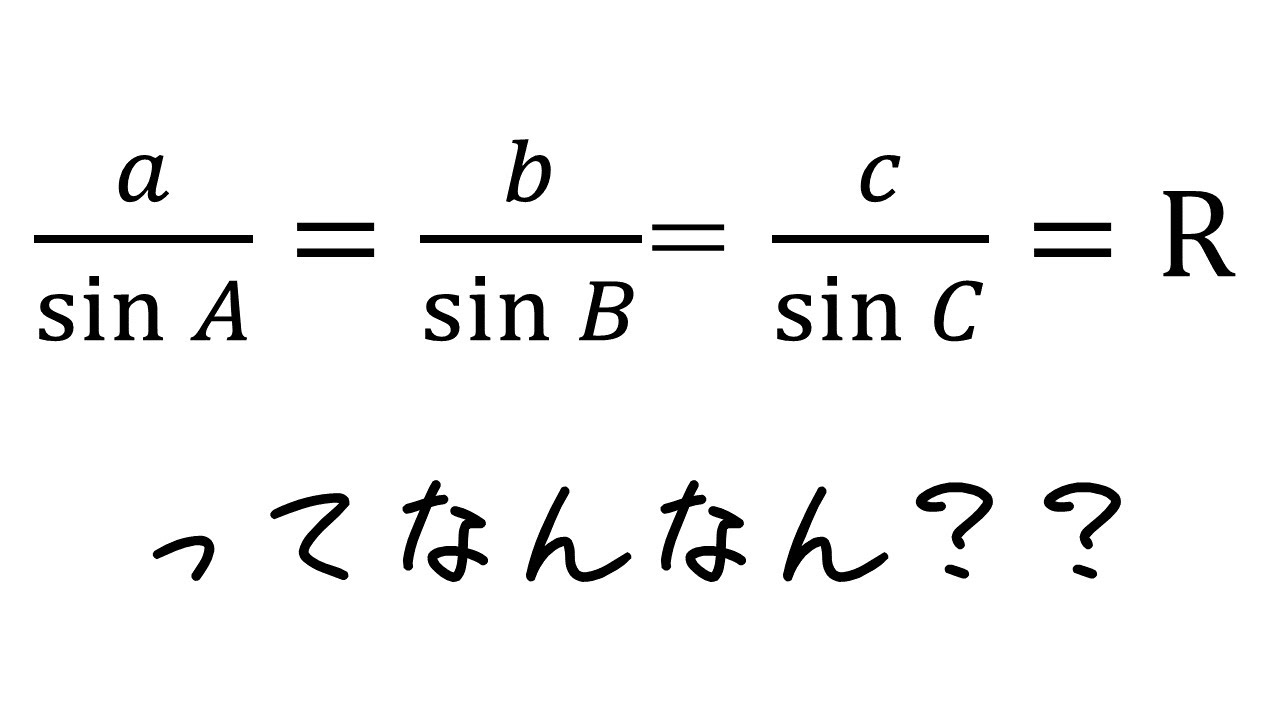問題文全文(内容文):
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
チャプター:
00:00~ 1問目
06:35~ 2問目
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
"$x,y,z$は実数とする。次の▢の中に、「必要十分条件であるが十分条件ではない」「十分条件であるが必要条件ではない」「必要十分条件である」「必要条件でも十分条件でもない」のうち、それぞれどれが適するか。
(1)$(x-y)(y-z)=0$は$x=y=z$であるための$\Box$
(2)$「x\gt 0 $かつ$y\gt 0」$は、$xy\gt 0$であるための$\Box$
(3)$x=y=0$は、$「xy=0$かつ$x+y=0」$であるための$\Box$
(4)$\angle A\lt 90$は$△ABC$が鋭角三角形であるための$\Box$
(5)$△ABC$の3辺$BC,CA,AB$の長さがそれぞれa$,b,c$とする。
$(a-b)(a^2+b^2=c^2)=0$は$△ABC$が直角二等辺三角形であるための$\Box$
$a,b$は実数とする。次の2つの条件$p,q$は同値であることを証明せよ。
$p:a\gt 1$かつ$b\gt 1$ $q:a+b\gt 2$かつ$(a-1)(b-1)\gt 0$
投稿日:2024.11.06