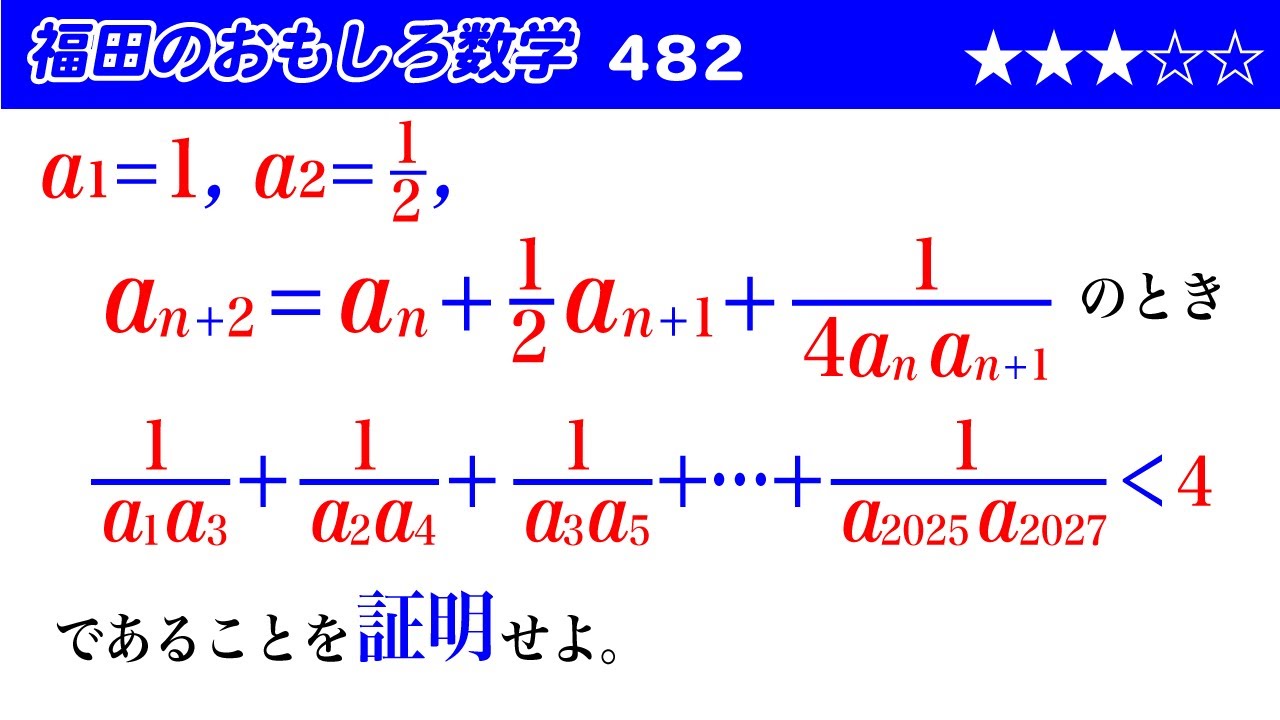
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
$\Large\boxed{5}$ a,bを$a^2$+$b^2$< 1を満たす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部になる2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)$f(\theta)$=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式$f(\theta)$=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも一つ存在することを示せ。
(2)Dの座標をa,θを用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも一つ存在することを示せ。また、このようなθはただ一つであることを示せ。
2023北海道大学理系過去問
投稿日:2023.04.10