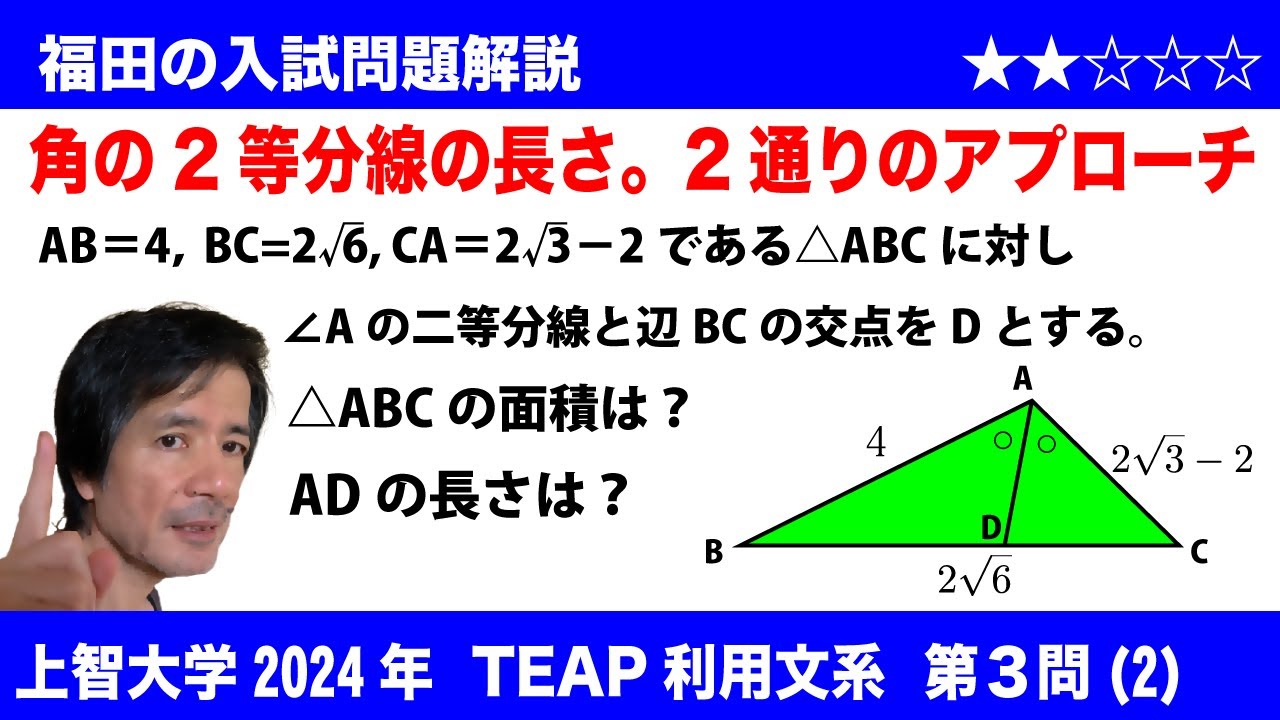
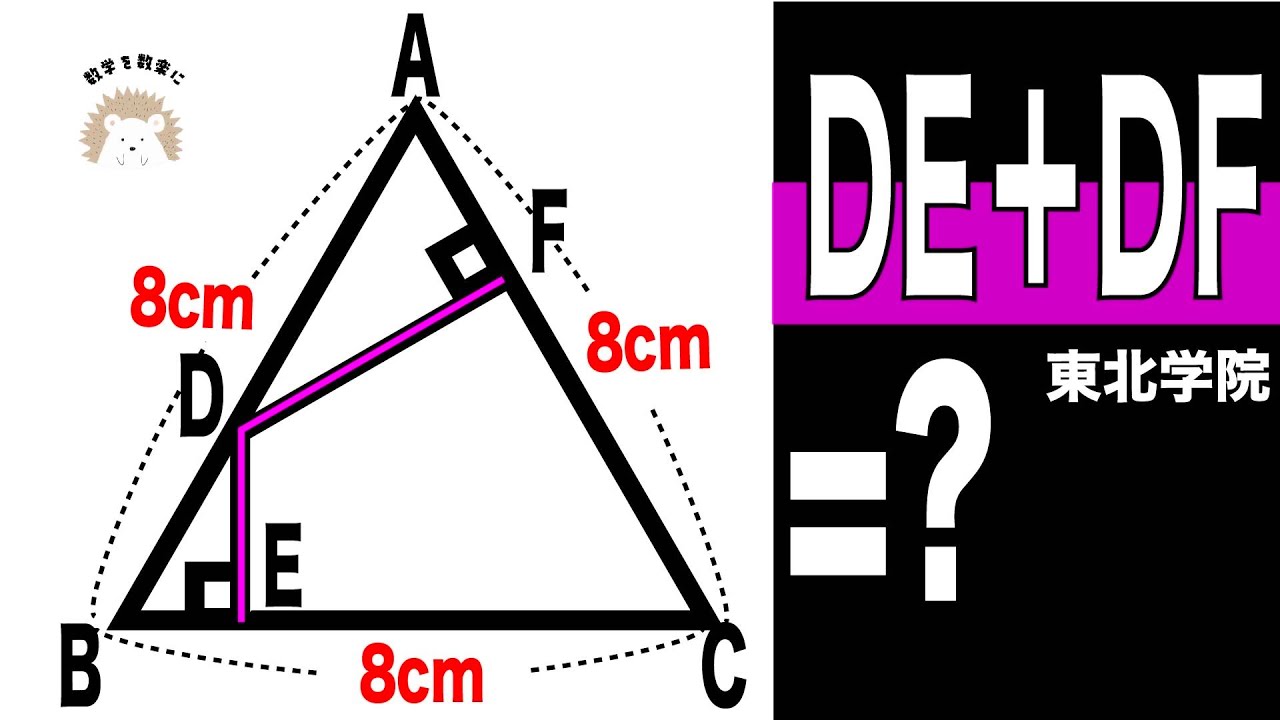
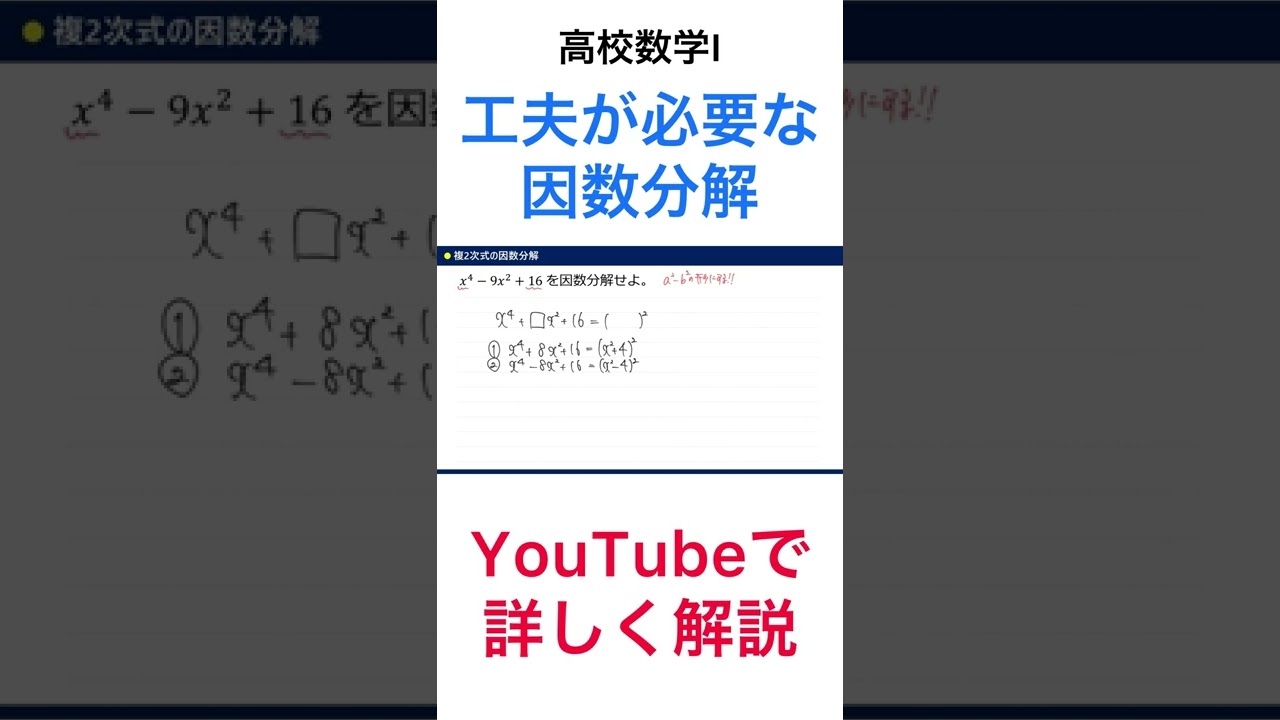
問題文全文(内容文):
1⃣
$x$は実数、$n$は自然数とする。次の命題の真偽を調べよ。
(a) $x \gt 1 \Rightarrow x \gt 0$
(b) $x \leqq -1 \Rightarrow |x| \gt 2$
(c) $|x| \leqq \Rightarrow |x-1| \lt 3$
(d) $n$は$18$の正の約数$\Rightarrow n$は$36$の正の約数
-----------------
2⃣
$x,y$は実数、$m$は整数とする。次の条件の否定を述べよ
(a) $x \neq 1$かつ$y = 4$
(b) $x \leqq 3$または$y \gt 7$
(c) $-1 \leqq x \lt -2$
(d) $m$は偶数または$3$の倍数である
(e) $x,y$はともに無理数である
1⃣
$x$は実数、$n$は自然数とする。次の命題の真偽を調べよ。
(a) $x \gt 1 \Rightarrow x \gt 0$
(b) $x \leqq -1 \Rightarrow |x| \gt 2$
(c) $|x| \leqq \Rightarrow |x-1| \lt 3$
(d) $n$は$18$の正の約数$\Rightarrow n$は$36$の正の約数
-----------------
2⃣
$x,y$は実数、$m$は整数とする。次の条件の否定を述べよ
(a) $x \neq 1$かつ$y = 4$
(b) $x \leqq 3$または$y \gt 7$
(c) $-1 \leqq x \lt -2$
(d) $m$は偶数または$3$の倍数である
(e) $x,y$はともに無理数である
チャプター:
00:00 はじまり
00:16 問題だよ
00:26 問題解説(1)
04:23 問題解説(2)
06:25 まとめ
06:42 まとめノート
単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$x$は実数、$n$は自然数とする。次の命題の真偽を調べよ。
(a) $x \gt 1 \Rightarrow x \gt 0$
(b) $x \leqq -1 \Rightarrow |x| \gt 2$
(c) $|x| \leqq \Rightarrow |x-1| \lt 3$
(d) $n$は$18$の正の約数$\Rightarrow n$は$36$の正の約数
-----------------
2⃣
$x,y$は実数、$m$は整数とする。次の条件の否定を述べよ
(a) $x \neq 1$かつ$y = 4$
(b) $x \leqq 3$または$y \gt 7$
(c) $-1 \leqq x \lt -2$
(d) $m$は偶数または$3$の倍数である
(e) $x,y$はともに無理数である
1⃣
$x$は実数、$n$は自然数とする。次の命題の真偽を調べよ。
(a) $x \gt 1 \Rightarrow x \gt 0$
(b) $x \leqq -1 \Rightarrow |x| \gt 2$
(c) $|x| \leqq \Rightarrow |x-1| \lt 3$
(d) $n$は$18$の正の約数$\Rightarrow n$は$36$の正の約数
-----------------
2⃣
$x,y$は実数、$m$は整数とする。次の条件の否定を述べよ
(a) $x \neq 1$かつ$y = 4$
(b) $x \leqq 3$または$y \gt 7$
(c) $-1 \leqq x \lt -2$
(d) $m$は偶数または$3$の倍数である
(e) $x,y$はともに無理数である
投稿日:2020.07.30