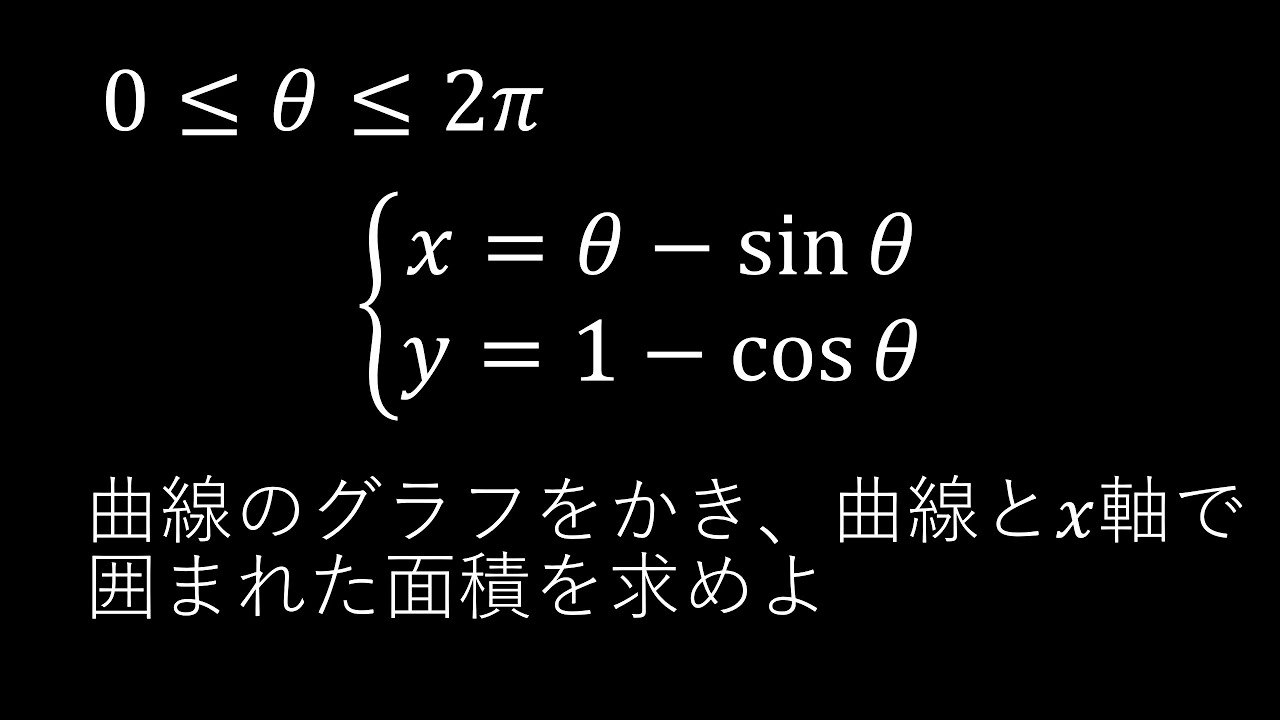問題文全文(内容文):
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
投稿日:2022.10.07