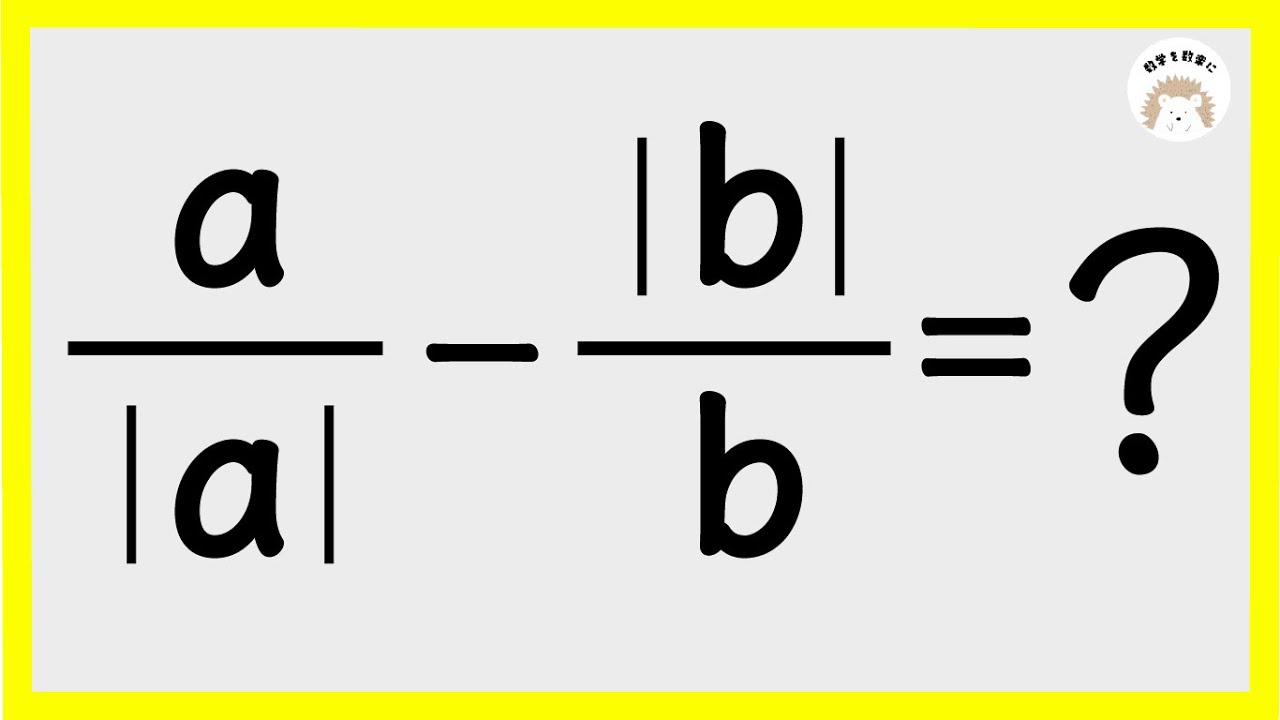問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
単元:
#数Ⅰ#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次方程式と2次不等式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
数学$\textrm{I}$ 絶対不等式(2)
ある実数$x$に対して
$ax^2 + 4x + a \gt 0$
が成り立つような$a$の値の範囲は?
投稿日:2021.05.03