【数Ⅲ】微分法：sinを微分するとどうなる？？グラフのイメージでサクッとわかる♪ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅲ > 微分とその応用 > 微分法 > 【数Ⅲ】微分法：sinを微分するとどうなる？？グラフのイメージでサクッとわかる♪

【数Ⅲ】微分法：sinを微分するとどうなる？？グラフのイメージでサクッとわかる♪

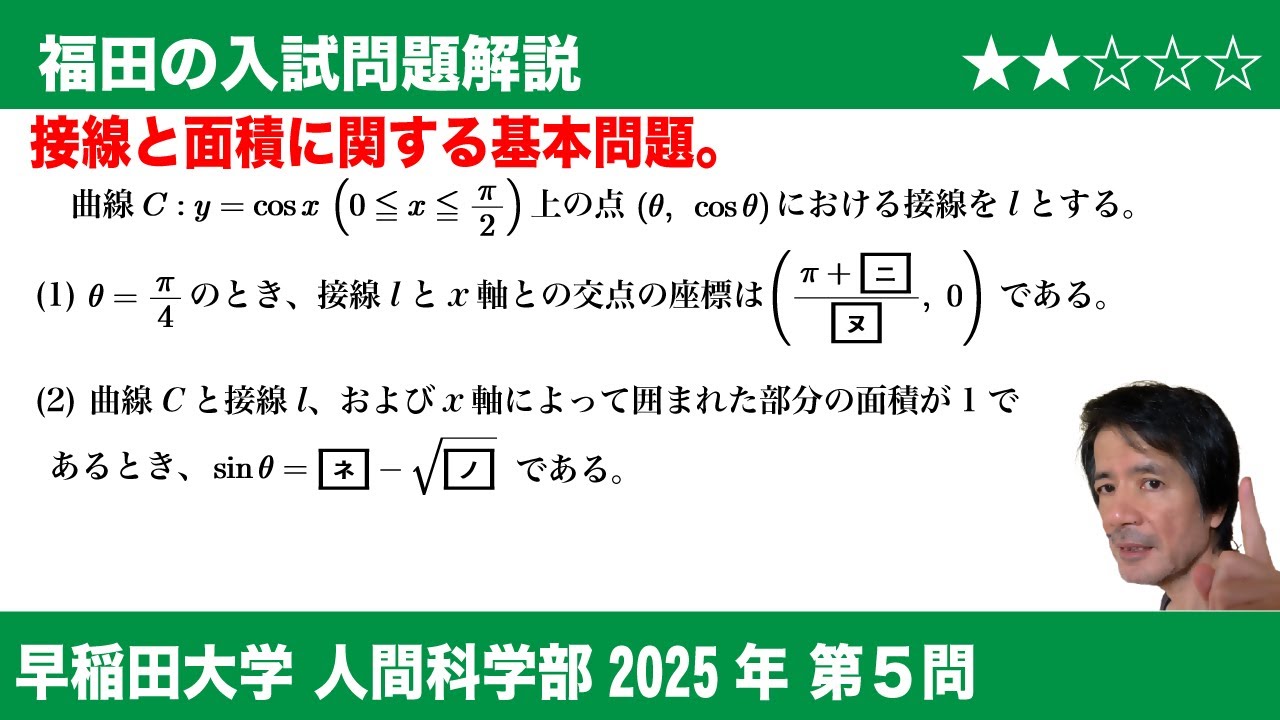
問題文全文(内容文)：
sinを微分するとどうなる？？
チャプター：

0:00 オープニング
0:12 sinの微分
2:16 cosの微分

単元： #微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師： 理数個別チャンネル
問題文全文(内容文)：
sinを微分するとどうなる？？
投稿日：2021.06.08

＜関連動画＞

福田のわかった数学〜高校３年生理系050〜極限(50)連続と微分可能(1)

アイキャッチ画像
単元： #関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#数Ⅲ
指導講師： 福田次郎
問題文全文(内容文)：
\begin{eqnarray}
数学\textrm{III}　連続と微分可能(1)\\
f(x)がx=aで微分可能 \Rightarrow f(x)はx=aで連続\\
を示せ。また、逆が成り立たないことを示せ。
\end{eqnarray}
この動画を見る　

中学生の知識でオイラーの公式を理解しよう　VOL ６　e ネイピア数の正体

アイキャッチ画像
単元： #数Ⅱ#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師： 鈴木貫太郎
この動画を見る　

答えが出ればいいか！？

アイキャッチ画像
単元： #微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$ x\gt 0とする.x^x=2^{2048}のxを求めよ.$
この動画を見る　

中学生の知識でオイラーの公式を理解しよう　VOL 5 対数　logの微分

アイキャッチ画像
単元： #微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師： 鈴木貫太郎
この動画を見る　

【理数個別の過去問解説】2021年度東京大学 数学 理科第3問(2)解説

アイキャッチ画像
単元： #大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師： 理数個別チャンネル
問題文全文(内容文)：
東京大学 2021年理科第３問（２）それぞれの項で分けて丁寧に積分せよ
関数
$f(x)=\dfrac{x}{x²+3}$
に対して、$y=f(x)$のグラフをCとする。点A($1,f(1)$)におけるCの接線を
$l:y=g(x)$
とする。
(1)Cとlの共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
(2)(1)で求めた共有点のx座標をαとする。定積分
$\displaystyle \int_{\alpha}^1{f(x)-g(x)}^2 dx$
を計算せよ。
この動画を見る　
PAGE TOP