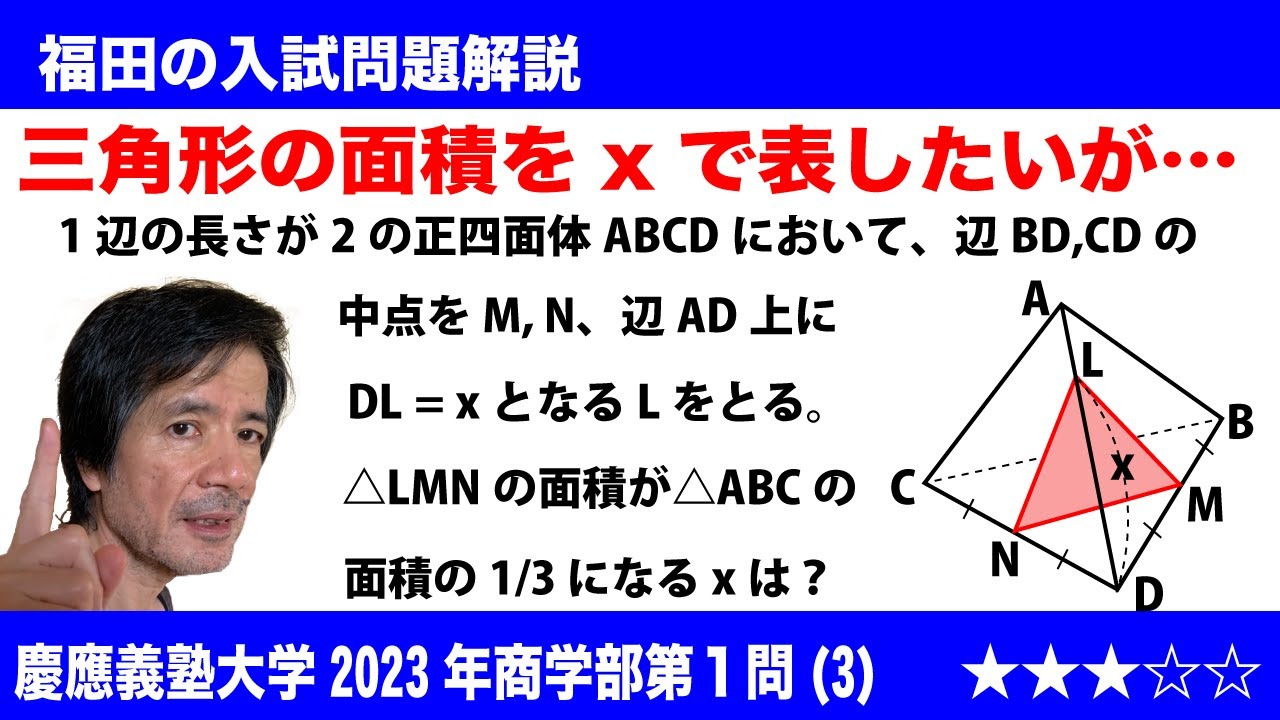
問題文全文(内容文):
(1) |$x$| + |$x-2$| $\lt x + 1$
(2)次の連立不等式を満たす整数$x$がちょうど3個存在するような定数$a$の値の
範囲を求めよ。
$\begin{eqnarray}
\begin{cases}
5x - 2 \gt 3x …①\\
x-a \lt 0 …②
\end{cases}
\end{eqnarray}$
(3) $ax + a \lt a^2 + x$ 解け。ただし、$a$は定数とする。
(1) |$x$| + |$x-2$| $\lt x + 1$
(2)次の連立不等式を満たす整数$x$がちょうど3個存在するような定数$a$の値の
範囲を求めよ。
$\begin{eqnarray}
\begin{cases}
5x - 2 \gt 3x …①\\
x-a \lt 0 …②
\end{cases}
\end{eqnarray}$
(3) $ax + a \lt a^2 + x$ 解け。ただし、$a$は定数とする。
チャプター:
00:00 はじまり
00:25 問題だよん
00:42 問題解説(1)
09:54 問題解説(2)
13:09 問題解説(3)
16:52 まとめ
17:21 問題と答え
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) |$x$| + |$x-2$| $\lt x + 1$
(2)次の連立不等式を満たす整数$x$がちょうど3個存在するような定数$a$の値の
範囲を求めよ。
$\begin{eqnarray}
\begin{cases}
5x - 2 \gt 3x …①\\
x-a \lt 0 …②
\end{cases}
\end{eqnarray}$
(3) $ax + a \lt a^2 + x$ 解け。ただし、$a$は定数とする。
(1) |$x$| + |$x-2$| $\lt x + 1$
(2)次の連立不等式を満たす整数$x$がちょうど3個存在するような定数$a$の値の
範囲を求めよ。
$\begin{eqnarray}
\begin{cases}
5x - 2 \gt 3x …①\\
x-a \lt 0 …②
\end{cases}
\end{eqnarray}$
(3) $ax + a \lt a^2 + x$ 解け。ただし、$a$は定数とする。
投稿日:2020.07.02