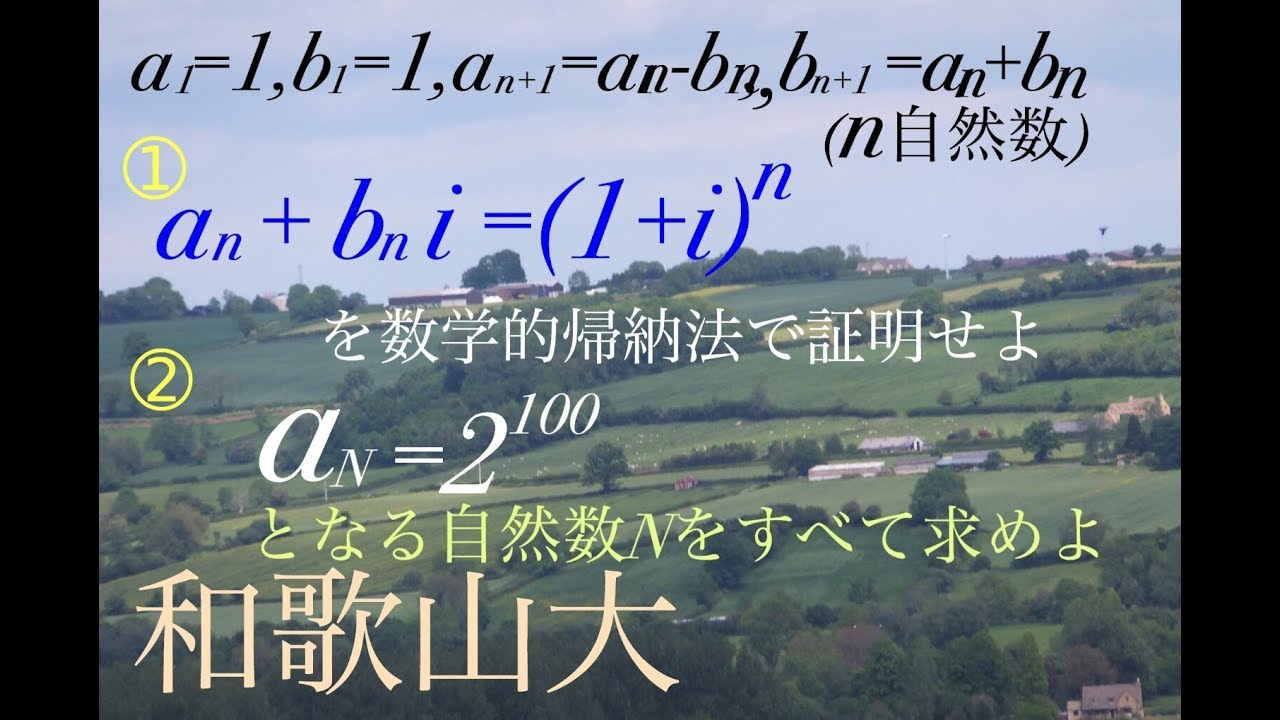2021北海道大連立漸化式 - 質問解決D.B.（データベース）

2021北海道大　連立漸化式

問題文全文(内容文)：

a_{1} = 2, b_{1} = 1

c_{n} = a_{n} b_{n}

a_{n + 1} = 2 a_{n} + 3 b_{n}

b_{n + 1} = a_{n} + 2 b_{n}

①

c_{2}

②

c_{n}

は偶数
③

n

が偶数なら

c_{n}

は28の倍数であることを示せ.

2021北海道大過去問

単元： #数列#漸化式#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：

a_{1} = 2, b_{1} = 1

c_{n} = a_{n} b_{n}

a_{n + 1} = 2 a_{n} + 3 b_{n}

b_{n + 1} = a_{n} + 2 b_{n}

①

c_{2}

②

c_{n}

は偶数
③

n

が偶数なら

c_{n}

は28の倍数であることを示せ.

2021北海道大過去問

投稿日：2021.02.28

＜関連動画＞

熊本大（理）漸化式

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
一般項を求めよ

a_{1} = \frac{1}{8}

(4 n^{2} - 1) (a_{n} - a_{n + 1}) ＝ 8 (n^{2} - 1) a_{n} a_{n + 1}

熊本大学理学部過去問

この動画を見る　

【高校数学】群数列を分かりやすく～どこよりも易しく丁寧に～ 3-13【数学Ｂ】

単元： #数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
1|3,5,7|9,11,13,15,17|19…
第n群の最初の数と最後の数を求めよ

この動画を見る　

高知大　漸化式高校数学 Mathematics Japanese university entrance exam

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
高知大学　過去問

初項

a_{1} = 4

、

(2 n + 2) a_{n} - n a_{(n + 1)} - 3 n - 6

(

n = 1, 2, 3, ・ ・ ・

)であるとき次の問いに答えよ。

(1)一般項

a_{n}

を求めよ

(2)

\sum_{k = 1}^{n} a_{k}

を求めよ

この動画を見る　

三重大　逆　漸化式 Mathematics Japanese university entrance exam

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：

a_{n} = \frac{1}{\sqrt{5}}

{

(\frac{5 + \sqrt{5}}{2})^{n} - (\frac{5 - \sqrt{5}}{2})^{n}

}

（1）

a_{n + 2}

を

a_{n + 1}, a_{n}

を用いて表せ

（2）

S_{n + 1}

を

a_{n}

の1次式で表せ

出典：1996年三重大学　過去問

この動画を見る　

数学「大学入試良問集」【13−5② 漸化式（デザイン型】を宇宙一わかりやすく

単元： #大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#滋賀大学

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：

a_{1} = 2, a_{n + 1 = 2 a_{n} - 2 a_{n} - 2 n + 1 (n = 1, 2, ・ ・ ・)}

によって定められる数列

{a_{n}}

について、次の問いに答えよ。

（1）

b_{n} = a_{n} - (α + β)

とおいて、数列

{b_{n}}

が等比数列になるように定数

α, β

の値を定めよ。

（2）
一般項

a_{n}

を求めよ。

（3）
初項から第

n

項までの和

S_{n} = \sum_{k = 1}^{n} a_{k}

を求めよ。

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 2021北海道大 連立漸化式

＜関連動画＞

熊本大（理）漸化式

【高校数学】群数列を分かりやすく～どこよりも易しく丁寧に～ 3-13【数学Ｂ】

高知大 漸化式 高校数学 Mathematics Japanese university entrance exam

三重大 逆 漸化式 Mathematics Japanese university entrance exam

数学「大学入試良問集」【13−5② 漸化式（デザイン型】を宇宙一わかりやすく