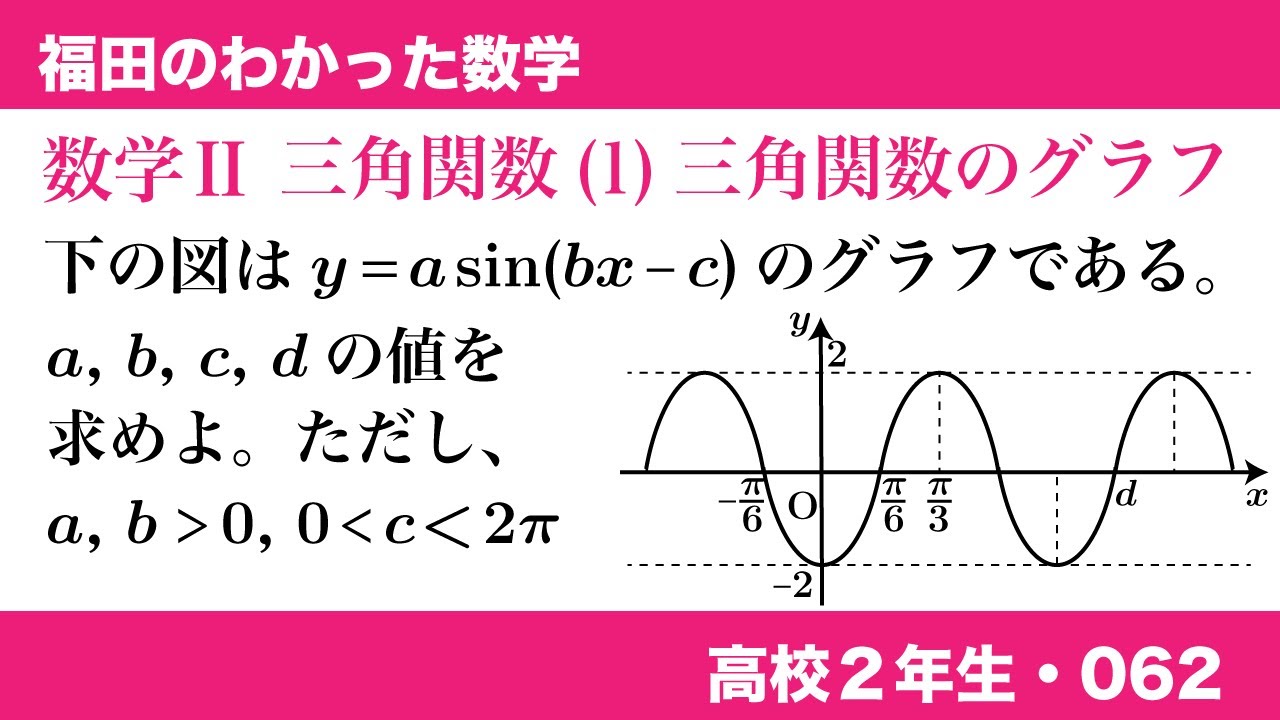
問題文全文(内容文):
$y=sinθ、y=cosθ、y=tanθ$のグラフを解説しました。
$y=sinθ、y=cosθ、y=tanθ$のグラフを解説しました。
チャプター:
0:00 オープニング
0:16 sinのグラフ
2:40 cosのグラフ
4:12 tanのグラフ
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$y=sinθ、y=cosθ、y=tanθ$のグラフを解説しました。
$y=sinθ、y=cosθ、y=tanθ$のグラフを解説しました。
投稿日:2021.01.20