x二乗をかけろ

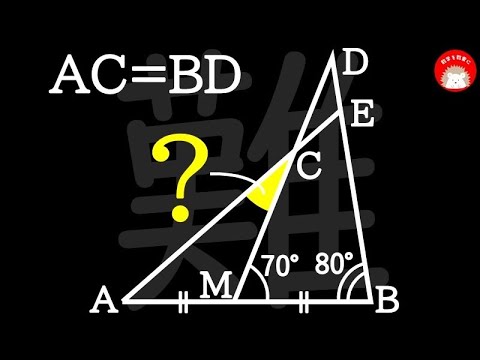
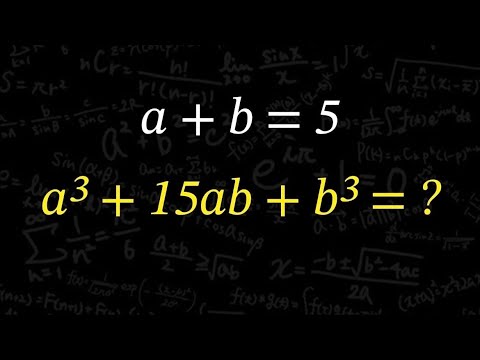問題文全文(内容文)：
$\frac{2x-4}{x} < 1$

単元： #数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$\frac{2x-4}{x} < 1$

投稿日：2023.04.04

単元： #数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
AB=6
斜線部の面積=?
＊図は動画内参照

この動画を見る　

単元： #数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
2つの長方形は合同
a：b=?
＊図は動画内参照

この動画を見る　

単元： #数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
2021学習院大学過去問題
$a,b$実数
$ax^2-3x+gt 0$
をみたすxの範囲が$a\lt x\lt a+1$
a,bの値

この動画を見る　

単元： #数Ⅰ#大学入試過去問(数学)#数と式#２次関数#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
実数$a,b,c$が
$a+b+c=8,a^2+b^2+c^2=32$
を満たす時、実数$c$の最大値を求めよ。

2014早稲田大過去問

この動画を見る　

単元： #数学(中学生)#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$(\sqrt {33} + \sqrt {21})(\sqrt {77} - 7)=$

久留米大附設高等学校

この動画を見る　