問題文全文(内容文)：
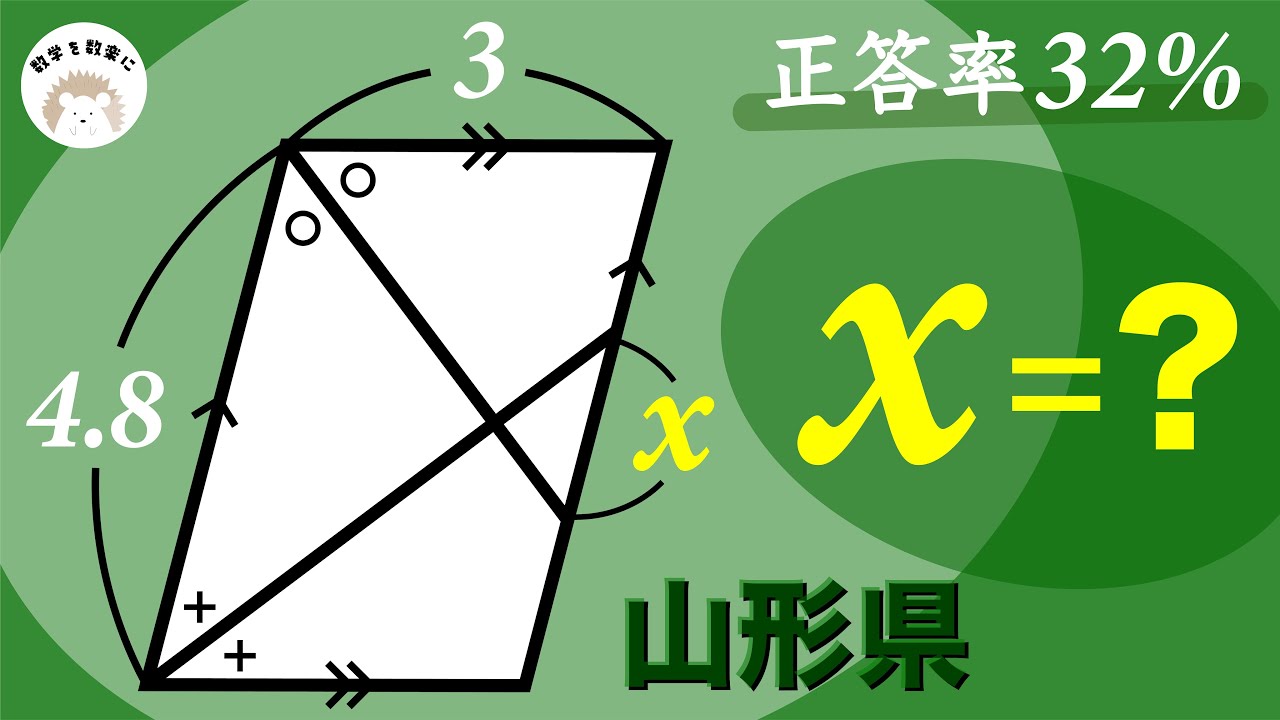
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#方べきの定理と２つの円の関係#数学オリンピック#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
投稿日：2024.02.16
