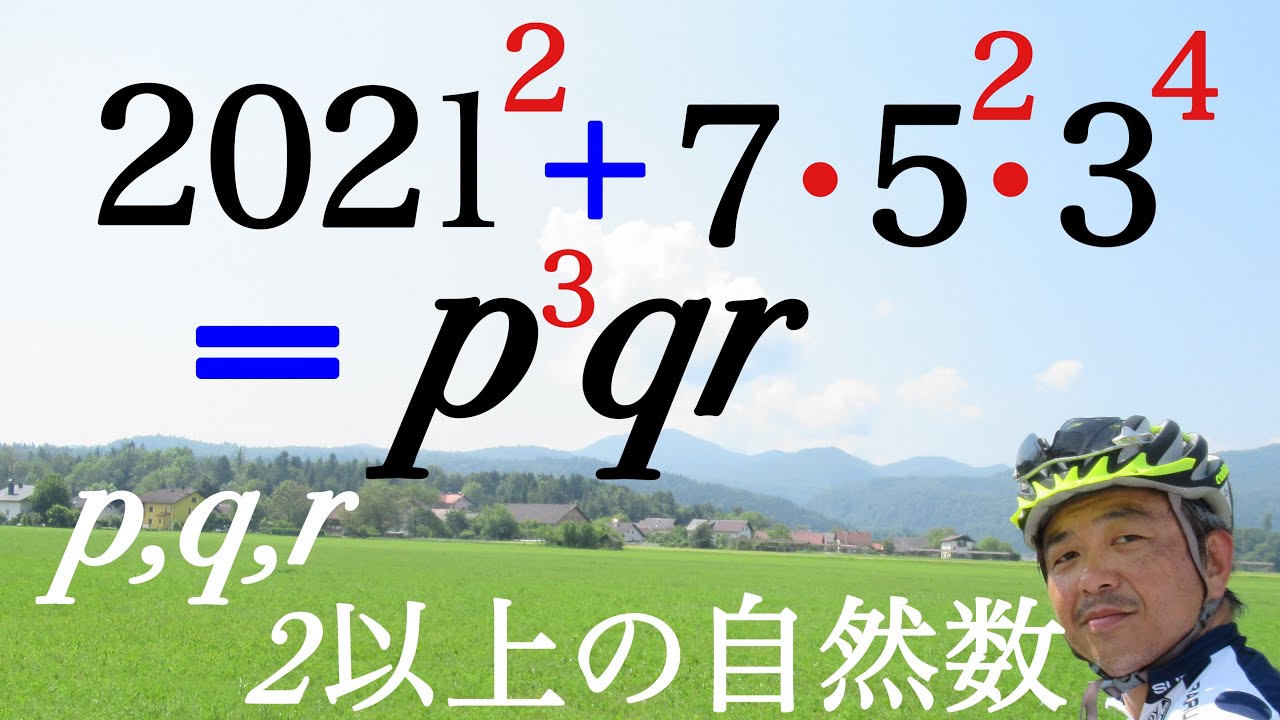問題文全文(内容文):
第4問
(1)$5^4=625$を$2^4$で割った時の余りは1に等しい。このことを用いると、不定方程式
$5^4x-2^4y=1 \ldots①$
の整数解のうち、xが正の整数で最小になるのは$x=\boxed{\ \ ア\ \ },y=\boxed{\ \ イウ\ \ }$であることがわかる。
また、①の整数解のうち、xが2桁の正の整数で最小になるのは
$x=\boxed{\ \ エオ\ \ }, y=\boxed{\ \ カキク\ \ }$である。
(2)次に、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りについて考えてみよう。
まず、
$625^2=5^{\boxed{ケ}}$
であり、また$m=\boxed{\ \ イウ\ \ }$とすると、$625^2=2^{\boxed{ケ}}\ m^2+2^{\boxed{コ}}\ m+1$である。
これらにより、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りがわかる。
(3)(2)の考察は、不定方程式
$5^5x-2^5y=1 \ldots②$
の整数解を調べるために利用できる。x,yを②の整数解とする。
$5^5x$は$5^5$の倍数であり、$2^5$で割った時の余りは1となる。よって(2)により、
$5^5x-625^2$は$5^5$でも$2^5$でも割り切れる。$5^5$と$2^5$は互いに素なので
$5^5x-625^2$は$5^5・2^5$の倍数である。このことから、②の整数解のうち、
xが3桁の正の整数で最小になるのは
$x=\boxed{\ \ サシス\ \ }, y=\boxed{\ \ セソタチツ\ \ }$
であることが分かる。
(4)$11^4$を$2^4$で割った時の余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、xが正の整数で最小になるのは
$x=\boxed{\ \ テト\ \ }, y=\boxed{\ \ ナニヌネノ\ \ }$ である。
2022共通テスト数学過去問
第4問
(1)$5^4=625$を$2^4$で割った時の余りは1に等しい。このことを用いると、不定方程式
$5^4x-2^4y=1 \ldots①$
の整数解のうち、xが正の整数で最小になるのは$x=\boxed{\ \ ア\ \ },y=\boxed{\ \ イウ\ \ }$であることがわかる。
また、①の整数解のうち、xが2桁の正の整数で最小になるのは
$x=\boxed{\ \ エオ\ \ }, y=\boxed{\ \ カキク\ \ }$である。
(2)次に、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りについて考えてみよう。
まず、
$625^2=5^{\boxed{ケ}}$
であり、また$m=\boxed{\ \ イウ\ \ }$とすると、$625^2=2^{\boxed{ケ}}\ m^2+2^{\boxed{コ}}\ m+1$である。
これらにより、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りがわかる。
(3)(2)の考察は、不定方程式
$5^5x-2^5y=1 \ldots②$
の整数解を調べるために利用できる。x,yを②の整数解とする。
$5^5x$は$5^5$の倍数であり、$2^5$で割った時の余りは1となる。よって(2)により、
$5^5x-625^2$は$5^5$でも$2^5$でも割り切れる。$5^5$と$2^5$は互いに素なので
$5^5x-625^2$は$5^5・2^5$の倍数である。このことから、②の整数解のうち、
xが3桁の正の整数で最小になるのは
$x=\boxed{\ \ サシス\ \ }, y=\boxed{\ \ セソタチツ\ \ }$
であることが分かる。
(4)$11^4$を$2^4$で割った時の余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、xが正の整数で最小になるのは
$x=\boxed{\ \ テト\ \ }, y=\boxed{\ \ ナニヌネノ\ \ }$ である。
2022共通テスト数学過去問
単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第4問
(1)$5^4=625$を$2^4$で割った時の余りは1に等しい。このことを用いると、不定方程式
$5^4x-2^4y=1 \ldots①$
の整数解のうち、xが正の整数で最小になるのは$x=\boxed{\ \ ア\ \ },y=\boxed{\ \ イウ\ \ }$であることがわかる。
また、①の整数解のうち、xが2桁の正の整数で最小になるのは
$x=\boxed{\ \ エオ\ \ }, y=\boxed{\ \ カキク\ \ }$である。
(2)次に、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りについて考えてみよう。
まず、
$625^2=5^{\boxed{ケ}}$
であり、また$m=\boxed{\ \ イウ\ \ }$とすると、$625^2=2^{\boxed{ケ}}\ m^2+2^{\boxed{コ}}\ m+1$である。
これらにより、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りがわかる。
(3)(2)の考察は、不定方程式
$5^5x-2^5y=1 \ldots②$
の整数解を調べるために利用できる。x,yを②の整数解とする。
$5^5x$は$5^5$の倍数であり、$2^5$で割った時の余りは1となる。よって(2)により、
$5^5x-625^2$は$5^5$でも$2^5$でも割り切れる。$5^5$と$2^5$は互いに素なので
$5^5x-625^2$は$5^5・2^5$の倍数である。このことから、②の整数解のうち、
xが3桁の正の整数で最小になるのは
$x=\boxed{\ \ サシス\ \ }, y=\boxed{\ \ セソタチツ\ \ }$
であることが分かる。
(4)$11^4$を$2^4$で割った時の余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、xが正の整数で最小になるのは
$x=\boxed{\ \ テト\ \ }, y=\boxed{\ \ ナニヌネノ\ \ }$ である。
2022共通テスト数学過去問
第4問
(1)$5^4=625$を$2^4$で割った時の余りは1に等しい。このことを用いると、不定方程式
$5^4x-2^4y=1 \ldots①$
の整数解のうち、xが正の整数で最小になるのは$x=\boxed{\ \ ア\ \ },y=\boxed{\ \ イウ\ \ }$であることがわかる。
また、①の整数解のうち、xが2桁の正の整数で最小になるのは
$x=\boxed{\ \ エオ\ \ }, y=\boxed{\ \ カキク\ \ }$である。
(2)次に、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りについて考えてみよう。
まず、
$625^2=5^{\boxed{ケ}}$
であり、また$m=\boxed{\ \ イウ\ \ }$とすると、$625^2=2^{\boxed{ケ}}\ m^2+2^{\boxed{コ}}\ m+1$である。
これらにより、$625^2$を$5^5$で割った時の余りと、$2^5$で割った時の余りがわかる。
(3)(2)の考察は、不定方程式
$5^5x-2^5y=1 \ldots②$
の整数解を調べるために利用できる。x,yを②の整数解とする。
$5^5x$は$5^5$の倍数であり、$2^5$で割った時の余りは1となる。よって(2)により、
$5^5x-625^2$は$5^5$でも$2^5$でも割り切れる。$5^5$と$2^5$は互いに素なので
$5^5x-625^2$は$5^5・2^5$の倍数である。このことから、②の整数解のうち、
xが3桁の正の整数で最小になるのは
$x=\boxed{\ \ サシス\ \ }, y=\boxed{\ \ セソタチツ\ \ }$
であることが分かる。
(4)$11^4$を$2^4$で割った時の余りは1に等しい。不定方程式
$11^5x-2^5y=1$
の整数解のうち、xが正の整数で最小になるのは
$x=\boxed{\ \ テト\ \ }, y=\boxed{\ \ ナニヌネノ\ \ }$ である。
2022共通テスト数学過去問
投稿日:2022.01.18