6年算数D-支援
6年算数D-支援
【受験算数】自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「100」までの番号の中で、発行されるものは何枚か。
(2)100人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「2888」と書かれたナンバープレートを受け取る人は何人目の人か。
この動画を見る
自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「100」までの番号の中で、発行されるものは何枚か。
(2)100人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「2888」と書かれたナンバープレートを受け取る人は何人目の人か。
【受験算数】自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「99」までの番号の中で、発行されるものは何枚になるか。
(2)99人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「777」と書かれたナンバープレートを受け取る人は何人目の人か。
この動画を見る
自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「99」までの番号の中で、発行されるものは何枚になるか。
(2)99人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「777」と書かれたナンバープレートを受け取る人は何人目の人か。
【受験算数】どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。
(2)0,3,6,7をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,3,6,7,30,33,…となる。このとき、3776ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べます。1,2,3,5,6,7,8,10,11,…このとき、100番目の数を求めよ。
この動画を見る
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。
(2)0,3,6,7をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,3,6,7,30,33,…となる。このとき、3776ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べます。1,2,3,5,6,7,8,10,11,…このとき、100番目の数を求めよ。
【受験算数】どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。
(2)0,2,8をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,2,8,20,22,…となる。このとき、2008ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べる。1,2,3,5,6,7,8,10,11,…このとき、40番目の数を求めよ。
この動画を見る
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。
(2)0,2,8をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,2,8,20,22,…となる。このとき、2008ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べる。1,2,3,5,6,7,8,10,11,…このとき、40番目の数を求めよ。
【受験算数】菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちる…【Part2】
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈412〉と表す。ただし、このケースには卵は215個までしか入りません。
(1)針が〈412〉となっているとき、何個の卵がケースに落ちたか。
(2)133個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
この動画を見る
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈412〉と表す。ただし、このケースには卵は215個までしか入りません。
(1)針が〈412〉となっているとき、何個の卵がケースに落ちたか。
(2)133個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
【受験算数】菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈243〉と表す。ただし、このケースには卵は124個までしか入らない。
(1)針が〈243〉となっているとき、何個の卵がケースに落ちたか。
(2)79個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
この動画を見る
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈243〉と表す。ただし、このケースには卵は124個までしか入らない。
(1)針が〈243〉となっているとき、何個の卵がケースに落ちたか。
(2)79個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
【受験算数】赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚…【Part2】
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は350cm²
(2)操作前の記号が(オ,9,5,4)のとき、操作後の記号は(3,2,カ,5)
この動画を見る
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は350cm²
(2)操作前の記号が(オ,9,5,4)のとき、操作後の記号は(3,2,カ,5)
【受験算数】赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚の…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は225cm²
(2)操作前の記号が(6,オ,3,7)のとき、操作後の記号は(カ,2,1,8)
この動画を見る
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は225cm²
(2)操作前の記号が(6,オ,3,7)のとき、操作後の記号は(カ,2,1,8)
【受験算数】右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が12個であるよう5列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
【受験算数】右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。(1)この外側のご石は何個か。(2)ご石の総数は何個か。
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
この動画を見る
右の図のように、内側の一辺が6個であるよう3列の中空方陣をご石で作り、くさり状につないだ。
(1)この外側のご石は何個か。
(2)ご石の総数は何個か。
【受験算数】ご石を図のようにならべて次々に正六角形を作る。(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
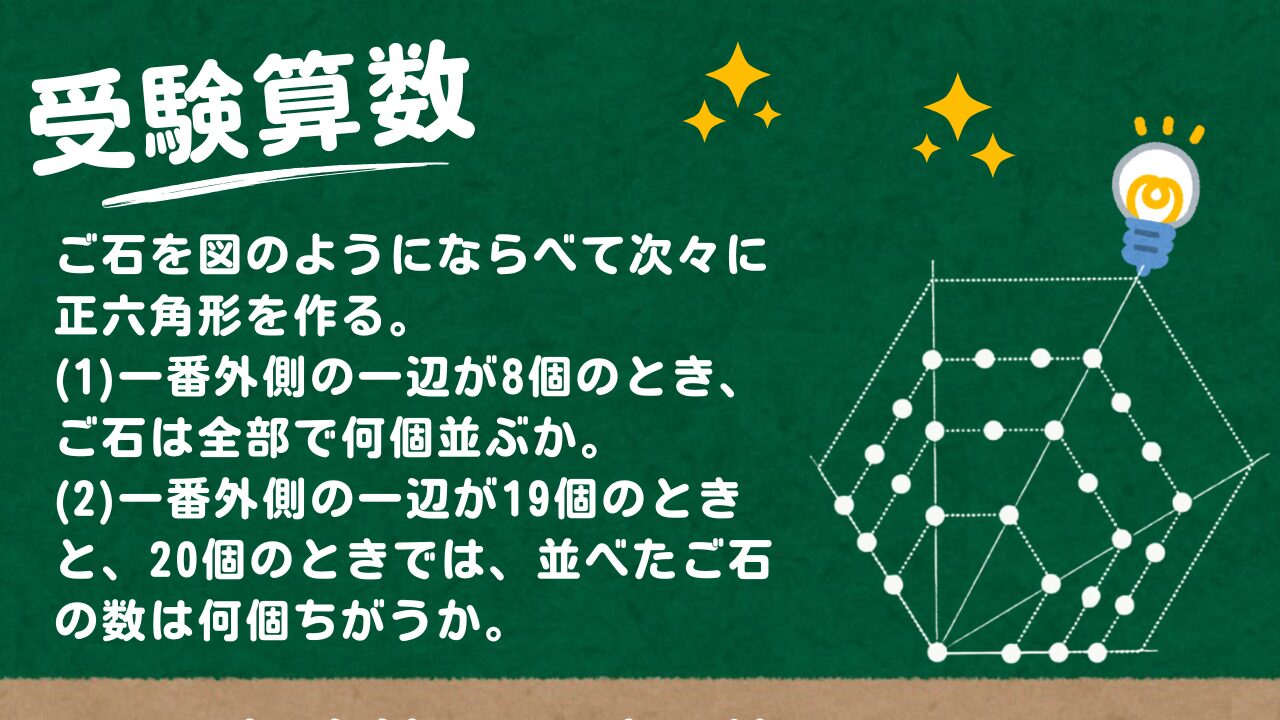
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正六角形を作る。
(1)一番外側の一辺が8個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が19個のときと、20個のときでは、並べたご石の数は何個ちがうか。
【受験算数】ご石を図のようにならべて次々に正五角形を作る。(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
この動画を見る
ご石を図のようにならべて次々に正五角形を作る。
(1)一番外側の一辺が9個のとき、ご石は全部で何個並ぶか。
(2)一番外側の一辺が16個のときと、17個のときでは、並べたご石の数は何個ちがうか。
【受験算数】長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には6mごとに、西側には8mごとに木を植える計画を立て、その分にあたるなえ木を61本買った。実際は、どちらの側にも7.5mごとに植えたので、なえ木が8本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えました。この土地の面積は何aか。
【受験算数】長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
この動画を見る
長方形の土地がある。この土地の北側には2mごとに、西側には4mごとに木を植える計画を立て、その分にあたるなえ木を81本買った。実際は、どちらの側にも5mごとに植えたので、なえ木が38本残った。土地のかどには必ずなえ木を植えるように計画し、実際に植えた。この土地の面積は何aか。
【受験算数】チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。このチョコレートを123個買った人が…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を6枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがあるとします。次の問いに答えよ。
(1)このチョコレートを123個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)300個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
【受験算数】チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。このチョコレートを35個買った人が、つつみ紙で引きかえ…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
この動画を見る
チョコレートのいちばん外側のつつみ紙を4枚集めると、新しいチョコレート1個といつでも引きかえられるようなチョコレートがある。
(1)このチョコレートを35個買った人が、つつみ紙で引きかえられるものはすべて引きかえるとすると、買ったものも合わせて全部で何個のチョコレートを手に入れることができるか。
(2)135個のチョコレートを手に入れるためには、少なくとも何個のチョコレートを買えばよいか。
【受験算数】一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたる…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
この動画を見る
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
【受験算数】一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたる…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
この動画を見る
一辺の長さが整数であるような正方形のたてと横を1cmはばに等分して、いくつかの小さな正方形にわける。左上のすみに1を書き、その下へ順に2,3,4,5,…という数を書き入れる。突きあたるごとに直角にまがり、うずまき状に進む。例えば(A)図は、一辺5cmの正方形について、この方法で書き入れたもの。(B)図は一辺がxcmの正方形について同じ方法で書き入れたものの一部だけを見せたもの。図(B)について、次の問いに答えよ。
(1)この正方形の一辺xcmを求めよ
(2)この正方形に書き入れてある数のうちで、いちばん大きい数は何か
(3)アのところに書いてある数は何か
【受験算数】 1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を3回くり返したとき、残っているカードは何枚か。このとき上から4枚目のカードに書かれた数はいくつか。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
この動画を見る
1から240までの数を書いたカード240枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、240枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を3回くり返したとき、残っているカードは何枚か。このとき上から4枚目のカードに書かれた数はいくつか。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
【受験算数】1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚の…
単元：
#算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を2回くり返したとき、残っているカードは何枚か。このとき上から5枚目のカードに書かれた数を答えよ。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
この動画を見る
1から127までの数を書いたカード127枚を上から数の小さい順に並べる。これをそのまま手にもって、上から順に左、右、左、右、...と交互に配り、配った順に上につみ重ねていって、127枚のカードを2つの山に分け、左側の山のカードは捨てて、右側の山のカードを再び数の小さい順に並べる。ここまでの操作を1回として、この操作をカードがなくなるまで続ける。
(1)この操作を2回くり返したとき、残っているカードは何枚か。このとき上から5枚目のカードに書かれた数を答えよ。
(2)この操作を何回くり返すと、残ったカードの数の和がはじめて400より小さくなるか。
(3)1枚のカードが残るまでに、何回この操作をくり返すか。そのカードに書かれた数を答えよ。
【受験算数】何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
この動画を見る
何人かの生徒が、いすに横一列に座っている。これから座り方を変えようと思う。全員が今までとは異なるいすに座る座り方は何通りあるか。以下のそれぞれの人数の場合について答えよ。ただし、いすは人数と同じ数だけある。
(1)3人のとき。
(2)4人のとき。
(3)5人のとき。
【受験算数】点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする…
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を10等分する点をA,B,C,D,E,F,G,H,I,Jとする。これらの点にさらに点Oを加えた11個の点から、3つの点をとりだし、これらを頂点とする三角形を作りたい。
(1)点Oを1つの頂点とする三角形は何個できるか。
(2)直角三角形は何個できるか。
(3)三角形は全部で何個作れるか。ただし、三角形ABFのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【受験算数】点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。正三角…
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
この動画を見る
点Oを中心とする円がある。この円の周囲を6等分する点をA,B,C,D,E,Fとする。これらの点にさらに点Oを加えた7個の点から、3つの点をとりだし、これらを頂点とする三角形を作る。
(1)正三角形は何個できるか。
(2)点Oを1つの頂点とする三角形は何個できるか。
(3)直角三角形は何個できるか。
(4)三角形は全部で何個作れるか。ただし、三角形ABDのように、三角形の一辺の上に点Oを含むものも、1つの三角形として数える。
【受験算数】たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,･･･,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば…
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
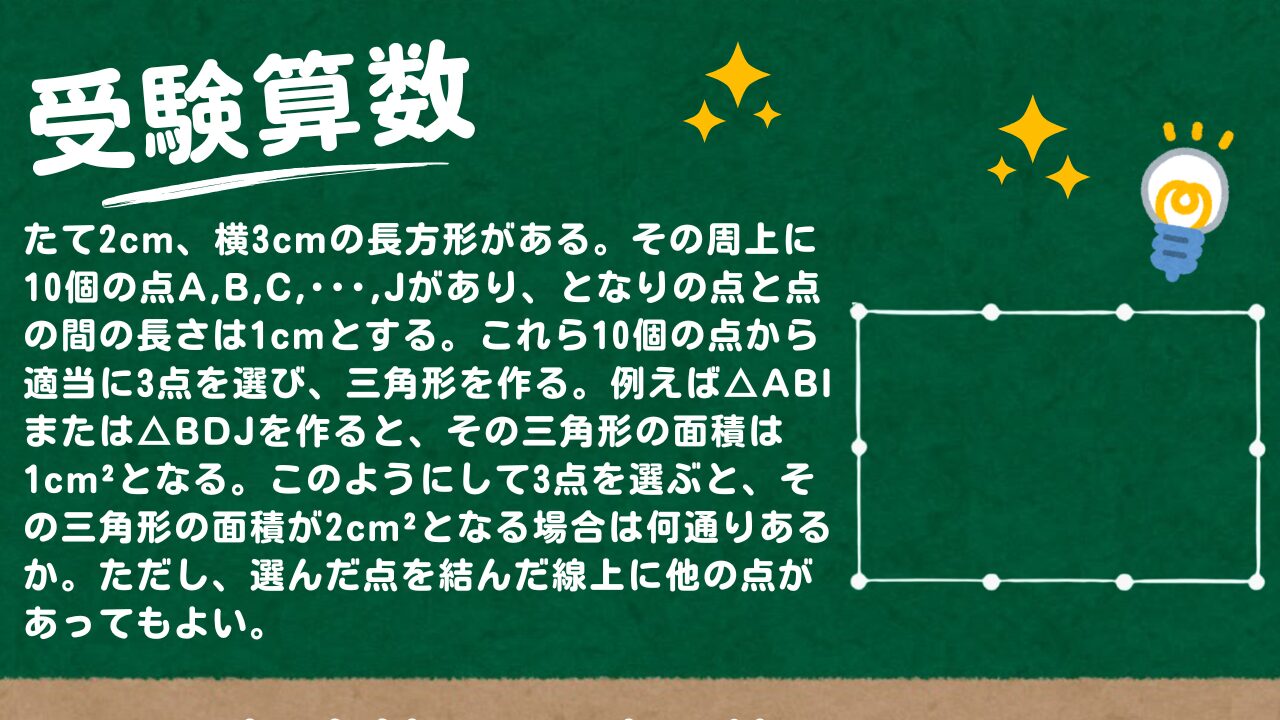
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,･･･,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横3cmの長方形がある。その周上に10個の点A,B,C,･･･,Jがあり、となりの点と点の間の長さは1cmとする。これら10個の点から適当に3点を選び、三角形を作る。例えば△ABIまたは△BDJを作ると、その三角形の面積は1cm²となる。このようにして3点を選ぶと、その三角形の面積が2cm²となる場合は何通りあるか。ただし、選んだ点を結んだ線上に他の点があってもよい。
【受験算数】たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,･･･,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACE…
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
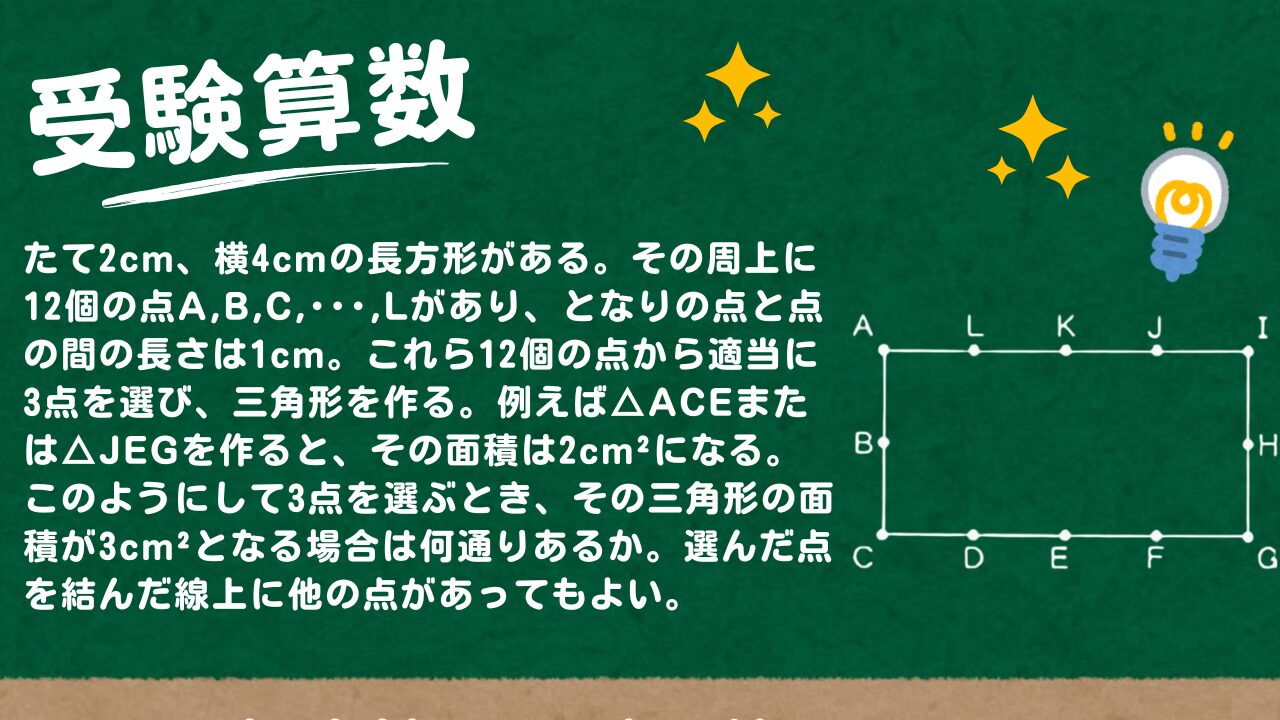
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,･･･,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
この動画を見る
たて2cm、横4cmの長方形がある。その周上に12個の点A,B,C,･･･,Lがあり、となりの点と点の間の長さは1cm。これら12個の点から適当に3点を選び、三角形を作る。例えば△ACEまたは△JEGを作ると、その面積は2cm²になる。このようにして3点を選ぶとき、その三角形の面積が3cm²となる場合は何通りあるか。選んだ点を結んだ線上に他の点があってもよい。
【受験算数】右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【受験算数】 右の図は一辺1cmの正方形を並べたもの。この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
単元：
#算数(中学受験)#場合の数#場合の数
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
この動画を見る
右の図は一辺1cmの正方形を並べたもの。
(1)この図のなかにはいろいろな大きさの正方形がある。正方形は全部で何個あるか。
(2)この図のなかにはいろいろな大きさの長方形がある。長方形(ただし、正方形は除く)は全部で何個あるか。
【受験算数】 東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから12.5秒後に線路の…
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから12.5秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ290m、225mで、速さの比が5:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの15秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
この動画を見る
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから12.5秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ290m、225mで、速さの比が5:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの15秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
【受験算数】 東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側…
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ240m、270mで、速さの比が4:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの18と3/4秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
この動画を見る
東西にのびる線路がある。ある時A君が線路の近くに立っていると、西から特急、東から急行が近づいてきて、A君のちょうど目の前ですれちがい始めた。すれちがい始めてから15秒後に線路の向こう側が見えた。特急と急行の列車の長さがそれぞれ240m、270mで、速さの比が4:3である。
(1)特急と急行の速さはそれぞれ秒速何mか。
(2)A君の真東にいたB君も同じ特急と急行を見ていた。B君の目の前を急行が通過し始めてから、特急が通過し終わるまでの18と3/4秒間はずっと線路の向こう側は見えないままだった。A君とB君の間の距離は何mか。
【受験算数】 川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたび…
単元：
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は4:5。モーターボートの静水時の速さと川の流れの速さを求めよ。
この動画を見る
川下のA地点から川上のB地点まで3km。Aを出た船が毎分20mの速さでBに向かって進むと、30分後に、川下から上ってきたモーターボートに追いこされた。それから20分後に、ふたたびモーターボートが下ってくるのに出会った。モーターボートは、Bで休まないで引き返し、川を上る速さと下る速さの比は4:5。モーターボートの静水時の速さと川の流れの速さを求めよ。