SPX
SPX
【受験算数】20mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは360m。しかし、A、Bの巻尺を正しいものさしで比較したら3mの差がありました。
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
20mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは360mとはかれました。しかし、A、Bの巻尺を正しいものさしで比較したら3mの差がありました。次の問いに答えなさい。
(1) Aの巻尺の20mは正しいものさしで何mですか。
(2) 2地点間の距離は実際は何mですか。
この動画を見る
20mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは360mとはかれました。しかし、A、Bの巻尺を正しいものさしで比較したら3mの差がありました。次の問いに答えなさい。
(1) Aの巻尺の20mは正しいものさしで何mですか。
(2) 2地点間の距離は実際は何mですか。
【受験算数】30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420m。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#SPX#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420mとはかれました。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。次の問いに答えなさい。
(1) Aの巻尺の30mは正しいものさしで何mですか。
(2) 2地点間の距離は実際は何mですか。
この動画を見る
30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420mとはかれました。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。次の問いに答えなさい。
(1) Aの巻尺の30mは正しいものさしで何mですか。
(2) 2地点間の距離は実際は何mですか。
【受験算数】長さ100mのA, B2個の巻尺で、2地点間の距離をはかる。Aではかった結果は4410mで、Bではかった結果は4680m。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら・・・
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
長さ100mのA, B2個の巻尺で、2地点間の距離をはかりました。Aではかった結果は4410mで、Bではかった結果は4680mでした。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら、正しいものさしで6.3mの差がありました。 次の問いに答えなさい。
(1) A、Bの巻尺を、それぞれ正しいものさしではかると、何mのくるいがありますか。
(2) Aの巻尺ではかって、1000mの距離は、正しいものさしではかれば何mですか。
この動画を見る
長さ100mのA, B2個の巻尺で、2地点間の距離をはかりました。Aではかった結果は4410mで、Bではかった結果は4680mでした。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら、正しいものさしで6.3mの差がありました。 次の問いに答えなさい。
(1) A、Bの巻尺を、それぞれ正しいものさしではかると、何mのくるいがありますか。
(2) Aの巻尺ではかって、1000mの距離は、正しいものさしではかれば何mですか。
【受験算数】長さ100mのA、B2個の巻尺で、2地点間の距離をはかる。Aではかった結果は4920m、Bではかった結果は5040m。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら・・・
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
長さ100mのA、B2個の巻尺で、2地点間の距離をはかった。Aではかった結果は4920m、Bではかった結果は5040mでした。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら、正しいものさしで2.4mの差がありました。
(1) A, Bの巻尺を、それぞれ正しいものさしではかると、何mのくるいがありますか。
(2) Aの巻尺ではかって、1000mの距離は、正しいものさしではかれば何mですか。
この動画を見る
長さ100mのA、B2個の巻尺で、2地点間の距離をはかった。Aではかった結果は4920m、Bではかった結果は5040mでした。この2つの巻尺には、少しくるいがあり、A、Bの長さを比べたら、正しいものさしで2.4mの差がありました。
(1) A, Bの巻尺を、それぞれ正しいものさしではかると、何mのくるいがありますか。
(2) Aの巻尺ではかって、1000mの距離は、正しいものさしではかれば何mですか。
【受験算数】ニュートン算：上下のパイプ
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
上、下にパイプのついた水そうに、ある量の水が入っています。それぞれ一定の割合で、上のバイブから水をつぎ込むと同時に、下のバイブから水を流して使用して行くと、ある時間で使い切ります。今、かりに、つぎこむ水の量を30%増し、使う水の量を10%増したとしても使い切る時間に変わりなく、またつぎ込む水の量を50%増し、使う水の量を20%増したとすると使い切る時間は3時間少なくなるそうです。
(1) 同じ時間に、つぎ込む水の量と、使う水の量の比を求めなさい。
(2) つぎ込む水の量を20%増し、使う水の量を変えないとしたら、使い切るまでの時間は、何時間ですか。
大問2
上、下にパイプのついた水そうに、ある量の水が入っています。それぞれ一定の割合で、上のバイブから水をつぎ込むと同時に、下のバイブから水を流して使用して行くと、ある時間で使い切ります。今、かりに、つぎこむ水の量を20%増し、使う水の量を10%増したとしても使い切る時間に変わりなく、またつぎ込む水の量を50%増し、使う水の量を20%増したとすると使い切る時間は2時間多くなるそうです。
(1) 同じ時間に、つぎ込む水の量と、使う水の量の比を求めなさい。
(2) つぎ込む水の量を20%増し、使う水の量を変えないとしたら、使い切るまで の時間は、何時間何分ですか。
この動画を見る
大問1
上、下にパイプのついた水そうに、ある量の水が入っています。それぞれ一定の割合で、上のバイブから水をつぎ込むと同時に、下のバイブから水を流して使用して行くと、ある時間で使い切ります。今、かりに、つぎこむ水の量を30%増し、使う水の量を10%増したとしても使い切る時間に変わりなく、またつぎ込む水の量を50%増し、使う水の量を20%増したとすると使い切る時間は3時間少なくなるそうです。
(1) 同じ時間に、つぎ込む水の量と、使う水の量の比を求めなさい。
(2) つぎ込む水の量を20%増し、使う水の量を変えないとしたら、使い切るまでの時間は、何時間ですか。
大問2
上、下にパイプのついた水そうに、ある量の水が入っています。それぞれ一定の割合で、上のバイブから水をつぎ込むと同時に、下のバイブから水を流して使用して行くと、ある時間で使い切ります。今、かりに、つぎこむ水の量を20%増し、使う水の量を10%増したとしても使い切る時間に変わりなく、またつぎ込む水の量を50%増し、使う水の量を20%増したとすると使い切る時間は2時間多くなるそうです。
(1) 同じ時間に、つぎ込む水の量と、使う水の量の比を求めなさい。
(2) つぎ込む水の量を20%増し、使う水の量を変えないとしたら、使い切るまで の時間は、何時間何分ですか。
【受験算数】水を満たした水そうに穴があります。今、水そうの水を10人では5時間でくみつくし、20人ならば3時間でくみつくします。この水そうを満水にして、そのままにしたら、何時間で水そうは空になりますか
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
水を満たした水そうに穴があります。今、水そうの水を10人では5時間でくみつくし、20人ならば3時間でくみつくします。それでは、この水そうを満水にして、そのままにしておいたら、何時間で水そうは空になりますか。
大問2
水を満たした水そうに穴があります。今、水そうの水を20人では4時間でくみつくし、30人ならば3時間でくみつくします。それでは、この水そうを満水にして、そのままにしておいたら、何時間で水そうは空になりますか。
この動画を見る
大問1
水を満たした水そうに穴があります。今、水そうの水を10人では5時間でくみつくし、20人ならば3時間でくみつくします。それでは、この水そうを満水にして、そのままにしておいたら、何時間で水そうは空になりますか。
大問2
水を満たした水そうに穴があります。今、水そうの水を20人では4時間でくみつくし、30人ならば3時間でくみつくします。それでは、この水そうを満水にして、そのままにしておいたら、何時間で水そうは空になりますか。
【受験算数】ニュートン算：途中で牛の数を変えると草はどうなる？
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
現在一定の草が生えている牧場では、100頭の牛を放すと48週間で食べつくしてしまい、125頭の牛を放すと36週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場には草がはえますか。
(2) この牧場で牛200頭を8週間放した後、ちょうど22週間食べさせるためには、 牛を何頭にすればよいですか。
大問2
現在一定の草が生えている牧場では、100頭の牛を放すと18週間で食べつくしてしまい、91頭の牛を放すと20週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場 には草がはえますか。
(2) この牧場で牛70頭を5週間放した後、ちょうど33週間食べさせるためには、牛を何頭にすればよいですか。
この動画を見る
大問1
現在一定の草が生えている牧場では、100頭の牛を放すと48週間で食べつくしてしまい、125頭の牛を放すと36週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場には草がはえますか。
(2) この牧場で牛200頭を8週間放した後、ちょうど22週間食べさせるためには、 牛を何頭にすればよいですか。
大問2
現在一定の草が生えている牧場では、100頭の牛を放すと18週間で食べつくしてしまい、91頭の牛を放すと20週間で食べつくしてしまいます。草は毎日一定の割合ではえ、牛はどの牛も1日に同じ量だけ草を食べるものとして、次の問いに答えなさい。
(1) 牛1頭が1週間に食べる草の量を1山とすると、1週間につき何山この牧場 には草がはえますか。
(2) この牧場で牛70頭を5週間放した後、ちょうど33週間食べさせるためには、牛を何頭にすればよいですか。
【受験算数】ニュートン算：駐車場の車の台数
単元：
#算数(中学受験)#文章題#仕事算とニュートン算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時48分に駐車場の車はなくなり、4分間に3台の割合で車が出ていくと、午後5時12分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)6分間に5台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
大問2
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時30分に駐車場の車はなくなり、8分間に5台の割合で車が出ていくと、午後7時20分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)7分間に4台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
この動画を見る
大問1
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時48分に駐車場の車はなくなり、4分間に3台の割合で車が出ていくと、午後5時12分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)6分間に5台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
大問2
ある駐車場に、午後2時に何台かの車が入っていて、しかも、毎分一定の割合で車が入ってきます。いま、3分間に2台の割合で車が出ていくと、午後6時30分に駐車場の車はなくなり、8分間に5台の割合で車が出ていくと、午後7時20分に駐車場の車はすっかりなくなります。
(1)午後2時に駐車していた車の台数を求めなさい。
(2)7分間に4台の割合で車が出ていくとき、午後何時何分に駐車場に車がいなくなりますか。
【受験算数】くるった時計（発展）A君の時計は何時をさしている？
単元：
#算数(中学受験)#速さ#点の移動・時計算#速さその他
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
A君とB君の2人は新幹線に乗りました。東京駅をちょうど14時に出発した列車が博多駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は19 時0分を、B君の時計は18時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① B君の時計はその日の12時の時報に合っていました。
② A君の時計はその日の16時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に10時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が12時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
大問2
A君とB君の2人は東北新幹線に乗りました。東京駅をちょうど14時に出発した列車が八戸駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は18 時0分を、B君の時計は16時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① A君の時計は前の日の22時の時報に合わせました。
② B君の時計はその日の10時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に8時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が1０時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
この動画を見る
大問1
A君とB君の2人は新幹線に乗りました。東京駅をちょうど14時に出発した列車が博多駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は19 時0分を、B君の時計は18時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① B君の時計はその日の12時の時報に合っていました。
② A君の時計はその日の16時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に10時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が12時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
大問2
A君とB君の2人は東北新幹線に乗りました。東京駅をちょうど14時に出発した列車が八戸駅に到着しました。列車がプラットホームに止まった瞬間、A君の時計は18 時0分を、B君の時計は16時0分をさしていました。A、B両君の時計でわかっていることは、次の①、②、③の3つです。
① A君の時計は前の日の22時の時報に合わせました。
② B君の時計はその日の10時の時報に合っていました。
③ A, B両君は、その日、2人の時計が同時に8時0分をさしているのを互いに確かめました。
このとき、次の問いに答えなさい。
(1) 正しい時計が1０時をさしているとき、A君の時計は何時何分をさしていますか。
(2) この列車が出発してから到着するまでにかかった時間は何時間何分ですか。
【受験算数】花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。その日の午後7時30分に和子の時計は何時何分？
単元：
#算数(中学受験)#速さ#点の移動・時計算#速さその他
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後7時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が10時をさしているとき、正しい時刻は何時何分ですか。
大問2
花子の時計は1日に正しい時計より10分おくれ、和子の時計は1日に15分進みます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後9時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が5時をさしているとき、正しい時刻は何時何分ですか。
この動画を見る
大問1
花子の時計は1日に正しい時計より40分進み、和子の時計は1日に30分おくれます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後7時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が10時をさしているとき、正しい時刻は何時何分ですか。
大問2
花子の時計は1日に正しい時計より10分おくれ、和子の時計は1日に15分進みます。ある日の正午に、2人の時計を正しい時刻に合わせました。次の問いに答えなさい。ただし、答えが整数にならないときは分数で答えなさい。
(1) その日の午後9時30分に和子の時計は何時何分をさしていますか。
(2) その日の午後、花子の時計が5時をさしているとき、正しい時刻は何時何分ですか。
【受験算数】速さ：到着しながら休む点の問題 点Pと点Qが出会うのは、出発してから何秒後？
単元：
#算数(中学受験)#速さ#ダイヤグラム#点の移動・時計算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは5秒間、点Qは3秒間休みます。ABの長さが90cm、点P、点Qの速さがそれぞれ毎秒６cm、毎秒４cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Aにはじめてもどったとき、点Qは点Aから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Aから何cmのところですか。
大問2
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは10秒間、点Qは4秒間休みます。ABの長さが360cm、点P、点Qの速さがそれぞれ毎秒8cm、毎秒3cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Bに2度目に到着したとき、点Qは点Bから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Bから何cmのところですか。
この動画を見る
大問1
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは5秒間、点Qは3秒間休みます。ABの長さが90cm、点P、点Qの速さがそれぞれ毎秒６cm、毎秒４cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Aにはじめてもどったとき、点Qは点Aから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Aから何cmのところですか。
大問2
右の図のように直線上に2つの点A,Bがあり、点Pと点Qが同時に点Aを出発してAB間を往復します。ただし、点A、点Bに到着するごとに、点Pは10秒間、点Qは4秒間休みます。ABの長さが360cm、点P、点Qの速さがそれぞれ毎秒8cm、毎秒3cmのとき、次の問いに答えなさい。
(1)点P、点Qが出発してからはじめて出会うのは何秒後ですか。
(2)点Pが点Bに2度目に到着したとき、点Qは点Bから何cmのところにいますか。
(3)点P、点Qが2度目に出会うのは、出発してから何秒後ですか。また、それは、点Bから何cmのところですか。
【受験算数】速さ：周期の利用 点Pと点Qが出会うのは、出発してから何秒後？
単元：
#算数(中学受験)#速さ#点の移動・時計算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
120cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて3秒間休み、これをくり返しながら進み、動いているときの速さは毎秒6cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
大問2
270cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて1秒間休み、これをくり返しながら進み、動いているときの速さは毎秒8cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
この動画を見る
大問1
120cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて3秒間休み、これをくり返しながら進み、動いているときの速さは毎秒6cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
大問2
270cmはなれた2点A、Bがあります。点PはAから、点QはBから同時に出発して、 PはBに、QはAに向かうものとします。このとき、点Pは3秒間動いて1秒間休み、 また3秒間動いて1秒間休むというように、これをくり返しながら進み、動いているときの速さは毎秒4cmです。点Qは5秒間動いて1秒間休み、これをくり返しながら進み、動いているときの速さは毎秒8cmです。このとき、次の問いに答えなさい。
(1) 点Pと点Qが出会うのは、出発してから何秒後ですか。
(2) 出会った点はAから何cmのところですか。
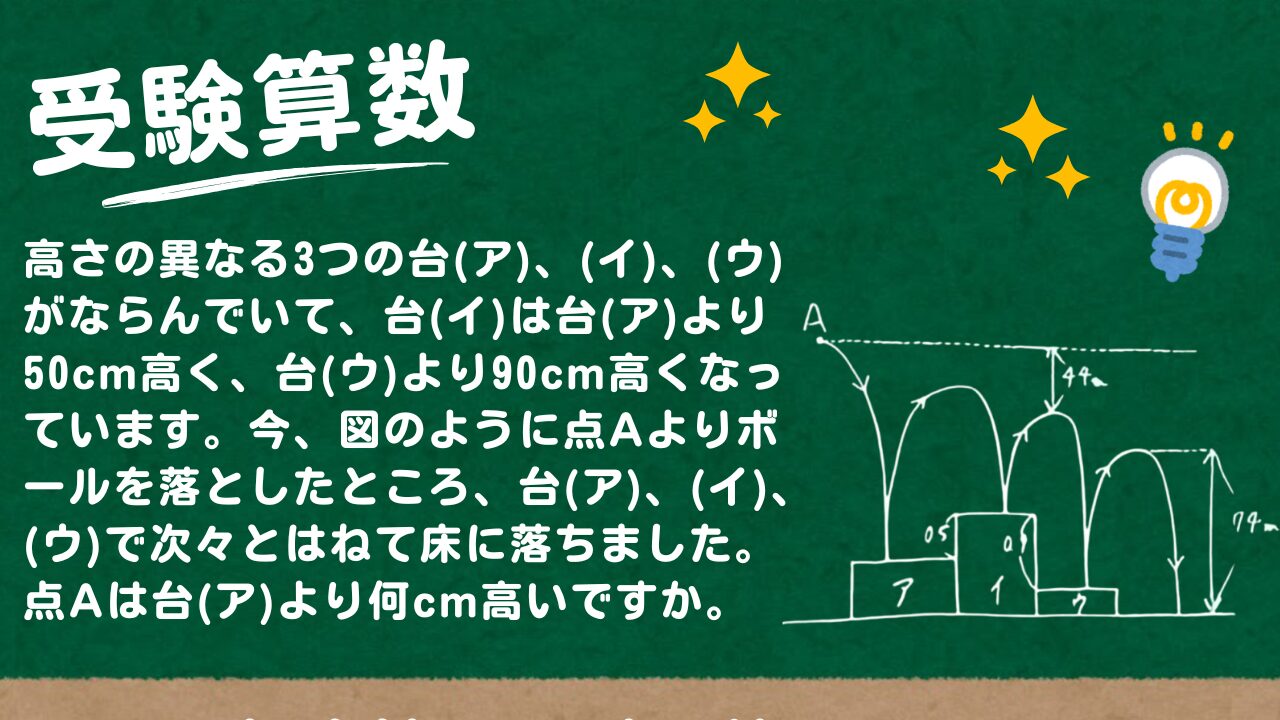
【受験算数】割合：ボールのはね上がりの処理
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
大問1
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より50cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより4.4m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら7.4mでした。ただし、このボールは落ちた高さの80%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
大問2
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より40cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより1.3m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら2.3mでした。ただし、このボールは落ちた高さの75%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
この動画を見る
大問1
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より50cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより4.4m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら7.4mでした。ただし、このボールは落ちた高さの80%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
大問2
高さの異なる3つの台(ア)、(イ)、(ウ)がならんでいて、台(イ)は台(ア)より40cm高く、台(ウ)より90cm高くなっています。今、図のように点Aよりボールを落としたところ、台(ア)、(イ)、(ウ)で次々とはねて床に落ちました。台(イ)ではねたあと、もっとも高くなった時の高さは、Aの高さより1.3m低く、台(ウ) ではねたあと、もっとも高くなった時の高さは、床か ら2.3mでした。ただし、このボールは落ちた高さの75%だけはねあがることとします。
(1)点Aは台(ア)より何cm高いですか。
(2)台(ア)の高さは何cmですか。
【受験算数】割合：等量交換2
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
容器Aには9%の食塩水が400g、容器Bには5%の食塩水が600g入っています。いま、2つの容器からそれぞれ同じ量の食塩水を同時に取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAにそれぞれ移しかえ、よくかき混ぜます。
(1) それぞれの容器から100gずつ取り出して交換すると、容器Aの食塩水の中に含まれる食塩の量は、最初に含まれていた食塩の量と比べて何g増えますか。 もしくは減りますか。
(2) 交換した後の容器AとBの食塩水の中に含まれる食塩の量を等しくするには、 AとBから何gずつの食塩水を取り出して交換すればよいですか。
(3) 交換して2つの容器の食塩水の濃さを等しくすると、濃さは何%になりますか。
この動画を見る
容器Aには9%の食塩水が400g、容器Bには5%の食塩水が600g入っています。いま、2つの容器からそれぞれ同じ量の食塩水を同時に取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAにそれぞれ移しかえ、よくかき混ぜます。
(1) それぞれの容器から100gずつ取り出して交換すると、容器Aの食塩水の中に含まれる食塩の量は、最初に含まれていた食塩の量と比べて何g増えますか。 もしくは減りますか。
(2) 交換した後の容器AとBの食塩水の中に含まれる食塩の量を等しくするには、 AとBから何gずつの食塩水を取り出して交換すればよいですか。
(3) 交換して2つの容器の食塩水の濃さを等しくすると、濃さは何%になりますか。
【受験算数】割合：等量交換1
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
容器Aには3%の食塩水が600g、容器Bには8%の食塩水が400g入っています。いま、2つの容器からそれぞれ同じ量の食塩水を同時に取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAにそれぞれ移しかえ、よくかき混ぜます。
(1) それぞれの容器から100gずつ取り出して交換すると、容器Aの食塩水の中に含まれる食塩の量は、最初に含まれていた食塩の量と比べて何g増えますか。 もしくは減りますか。
(2) 交換した後の容器AとBの食塩水の中に含まれる食塩の量を等しくするには、 AとBから何gずつの食塩水を取り出して交換すればよいですか。
(3) 交換して2つの容器の食塩水の濃さを等しくすると、濃さは何%になりますか。
この動画を見る
容器Aには3%の食塩水が600g、容器Bには8%の食塩水が400g入っています。いま、2つの容器からそれぞれ同じ量の食塩水を同時に取り出し、Aから取り出した食塩水はBに、Bから取り出した食塩水はAにそれぞれ移しかえ、よくかき混ぜます。
(1) それぞれの容器から100gずつ取り出して交換すると、容器Aの食塩水の中に含まれる食塩の量は、最初に含まれていた食塩の量と比べて何g増えますか。 もしくは減りますか。
(2) 交換した後の容器AとBの食塩水の中に含まれる食塩の量を等しくするには、 AとBから何gずつの食塩水を取り出して交換すればよいですか。
(3) 交換して2つの容器の食塩水の濃さを等しくすると、濃さは何%になりますか。
【受験算数】割合：やりとり2
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
容器Aには12%の食塩水が400g、容器Bには10%の食塩水が300g入っています。
まず、容器Aの中の食塩水を100g取り出して、容器Bに移し、よくかき混ぜました。 その後、容器Bから200gの食塩水を取り出して、容器Aに移したところ、容器Aの食塩水の濃さは① %、容器Bの食塩水の濃さは②%になりました。
この動画を見る
容器Aには12%の食塩水が400g、容器Bには10%の食塩水が300g入っています。
まず、容器Aの中の食塩水を100g取り出して、容器Bに移し、よくかき混ぜました。 その後、容器Bから200gの食塩水を取り出して、容器Aに移したところ、容器Aの食塩水の濃さは① %、容器Bの食塩水の濃さは②%になりました。
【受験算数】割合：やりとり1
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
容器Aには5%の食塩水が360g、容器Bには14%の食塩水が600g入っています。
まず、容器Aの中の食塩水を120g取り出して、容器Bに移し、よくかき混ぜました。 その後、容器Bから360gの食塩水を取り出して、容器Aに移したところ、容器Aの食塩水の濃さは① %、容器Bの食塩水の濃さは②%になりました。
この動画を見る
容器Aには5%の食塩水が360g、容器Bには14%の食塩水が600g入っています。
まず、容器Aの中の食塩水を120g取り出して、容器Bに移し、よくかき混ぜました。 その後、容器Bから360gの食塩水を取り出して、容器Aに移したところ、容器Aの食塩水の濃さは① %、容器Bの食塩水の濃さは②%になりました。
【受験算数】割合：出し入れ(2)2
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
8%の食塩水が225gあります。これから50gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は45gを取り出し、水を44g 入れると、何%の食塩水になりますか。
この動画を見る
8%の食塩水が225gあります。これから50gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は45gを取り出し、水を44g 入れると、何%の食塩水になりますか。
【受験算数】割合：出し入れ(2)1
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
15%の食塩水が100gあります。これから40gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は55gを取り出し、水を20g 入れると、何%の食塩水になりますか。
この動画を見る
15%の食塩水が100gあります。これから40gの食塩水を取り出して、そのかわりに水を50g入れ、こうしてできた食塩水から、今度は55gを取り出し、水を20g 入れると、何%の食塩水になりますか。
【受験算数】割合：出し入れ(1)2
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
水120gに食塩30gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を25ｇくみ出して捨て、そのあと、水15ｇを加えてよく混ぜ合わせました。
そして、その食塩水を56ｇ取り出しました。取り出した食塩水56ｇの中には、食塩が何ｇ溶けていますか？
この動画を見る
水120gに食塩30gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を25ｇくみ出して捨て、そのあと、水15ｇを加えてよく混ぜ合わせました。
そして、その食塩水を56ｇ取り出しました。取り出した食塩水56ｇの中には、食塩が何ｇ溶けていますか？
【受験算数】水90gに食塩10gを溶かし、混ぜ合わせた食塩水100gがあります。この食塩水を40ｇ捨て、水30ｇを加えて混ぜ合わせました。そこから取り出した食塩水30ｇには、食塩が何ｇ溶けていますか？
単元：
#算数(中学受験)#文章題#売買損益と食塩水
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
水90gに食塩10gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を40ｇくみ出して捨て、そのあと、水30ｇを加えてよく混ぜ合わせました。
そして、その食塩水を30ｇ取り出しました。取り出した食塩水30ｇの中には、食塩が何ｇ溶けていますか？
この動画を見る
水90gに食塩10gを溶かし、よく混ぜ合わせた食塩水100gがあります。この食塩水を40ｇくみ出して捨て、そのあと、水30ｇを加えてよく混ぜ合わせました。
そして、その食塩水を30ｇ取り出しました。取り出した食塩水30ｇの中には、食塩が何ｇ溶けていますか？
【受験算数】平面図形総合：相似をつくる
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
下の三角形ABCの面積は100cm²で、辺上の各点は、各辺を4等分する点です。 三角形BCDの面積を求めなさい。
この動画を見る
下の三角形ABCの面積は100cm²で、辺上の各点は、各辺を4等分する点です。 三角形BCDの面積を求めなさい。
【受験算数】平面図形総合：折り返す
単元：
#算数(中学受験)#平面図形#平面図形その他
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
たて10cm、横26cmの長方形の形をした紙ABCDを、頂点B が辺AD上に点FにくるようにCEで折り返したところ、 AFの長さが2cmになりました。BEの長さを求めなさい。
この動画を見る
たて10cm、横26cmの長方形の形をした紙ABCDを、頂点B が辺AD上に点FにくるようにCEで折り返したところ、 AFの長さが2cmになりました。BEの長さを求めなさい。
【受験算数】平面図形総合：直角三角形の相似 線分比は？
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のように、直角三角形ABCに正方形DEFGがぴったり収まっています。 BE:EF: FCを最も簡単な整数の比で求めなさい。
この動画を見る
図のように、直角三角形ABCに正方形DEFGがぴったり収まっています。 BE:EF: FCを最も簡単な整数の比で求めなさい。
【受験算数】平面図形総合：相似をつくる
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
四角形ABCDは辺の長さが12cmの正方形で、辺上の各点は、各辺を4等分する点です。斜線部分の面積を求めなさい。
この動画を見る
四角形ABCDは辺の長さが12cmの正方形で、辺上の各点は、各辺を4等分する点です。斜線部分の面積を求めなさい。
【受験算数】平面図形総合：相似を見つける2
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
高さ7cmの平行四辺形ABCDがあり、ADの長さは10cmです。点Eは辺BC上 の点で、BEの長さは4㎝です。以下の各問いに答えなさい。
(1) AF: FEを最も簡単な整数の比で答えなさい。
(2) AG:GCを最も簡単な整数の比で答えなさい。
(3) 三角形AFGの面積を答えなさい。
この動画を見る
高さ7cmの平行四辺形ABCDがあり、ADの長さは10cmです。点Eは辺BC上 の点で、BEの長さは4㎝です。以下の各問いに答えなさい。
(1) AF: FEを最も簡単な整数の比で答えなさい。
(2) AG:GCを最も簡単な整数の比で答えなさい。
(3) 三角形AFGの面積を答えなさい。
【受験算数】平面図形総合：台形の面積比
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
図のような台形ABCDの辺AB上に点Eを、辺DC上に点Fを取ったところ。 EFはADと平行になりました。次の各問いに答えなさい。
(1) EFの長さは何cmですか。
(2) 四角形AEFDと四角形EBCFの面積の・ 比を最も簡単な整数の比で求めなさい。
この動画を見る
図のような台形ABCDの辺AB上に点Eを、辺DC上に点Fを取ったところ。 EFはADと平行になりました。次の各問いに答えなさい。
(1) EFの長さは何cmですか。
(2) 四角形AEFDと四角形EBCFの面積の・ 比を最も簡単な整数の比で求めなさい。
【受験算数】平面図形総合：平行四辺形の面積比2
単元：
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
四角形ABCDは平行四辺形で、辺上の各点は、辺ADを4等分する点、辺BC を5等分する点です。平行四辺形ABCDの面積と斜線部分の面積の池を最も簡単 な整数の比で求めなさい。
この動画を見る
四角形ABCDは平行四辺形で、辺上の各点は、辺ADを4等分する点、辺BC を5等分する点です。平行四辺形ABCDの面積と斜線部分の面積の池を最も簡単 な整数の比で求めなさい。
【受験算数】文章題：割合、等量を加減する1
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材：
#SPX#5年算数D-支援#中学受験教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
花子さんは400円、春子さんは150円持っています。今日、2人はお母さんから同じ金額をもらったので、花子さんの持っているお金は春子さんの12/7倍になりました。 花子さんがお母さんからもらったお金はいくらですか。
この動画を見る
花子さんは400円、春子さんは150円持っています。今日、2人はお母さんから同じ金額をもらったので、花子さんの持っているお金は春子さんの12/7倍になりました。 花子さんがお母さんからもらったお金はいくらですか。
【受験算数】文章題：割合、等量からの変化2
単元：
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
教材：
#SPX#中学受験教材#6年算数D-支援
指導講師：
理数個別チャンネル
問題文全文(内容文)：
AとBは同じ金額を持っていましたが、Aは650円もらい、Bは350円使ったので、 Aの所持金はBの所持金の7倍より200円少なくなりました。 現在、Bはいくら持っていますか。
この動画を見る
AとBは同じ金額を持っていましたが、Aは650円もらい、Bは350円使ったので、 Aの所持金はBの所持金の7倍より200円少なくなりました。 現在、Bはいくら持っていますか。