 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
あきとんとん本の予約が開始だってよ~15万人記念~

【中学数学】方程式の基礎をどこよりも丁寧に 3-1【中1数学】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)次の方程式のうち3が解であるものをすべて選べ
①$3x+2=11$ ②$\frac{1}{3}x+4=7$ ③$-2x+1=10$ ④$\frac{1}{6}x+\frac{1}{2}=1$
(2)次の方程式を解け
①$x-5=-7$ ②$2x=4$ ③$3x+4=-8$
この動画を見る
(1)次の方程式のうち3が解であるものをすべて選べ
①$3x+2=11$ ②$\frac{1}{3}x+4=7$ ③$-2x+1=10$ ④$\frac{1}{6}x+\frac{1}{2}=1$
(2)次の方程式を解け
①$x-5=-7$ ②$2x=4$ ③$3x+4=-8$
【中学数学】方程式の基礎をどこよりも丁寧に 3-1【中1数学】

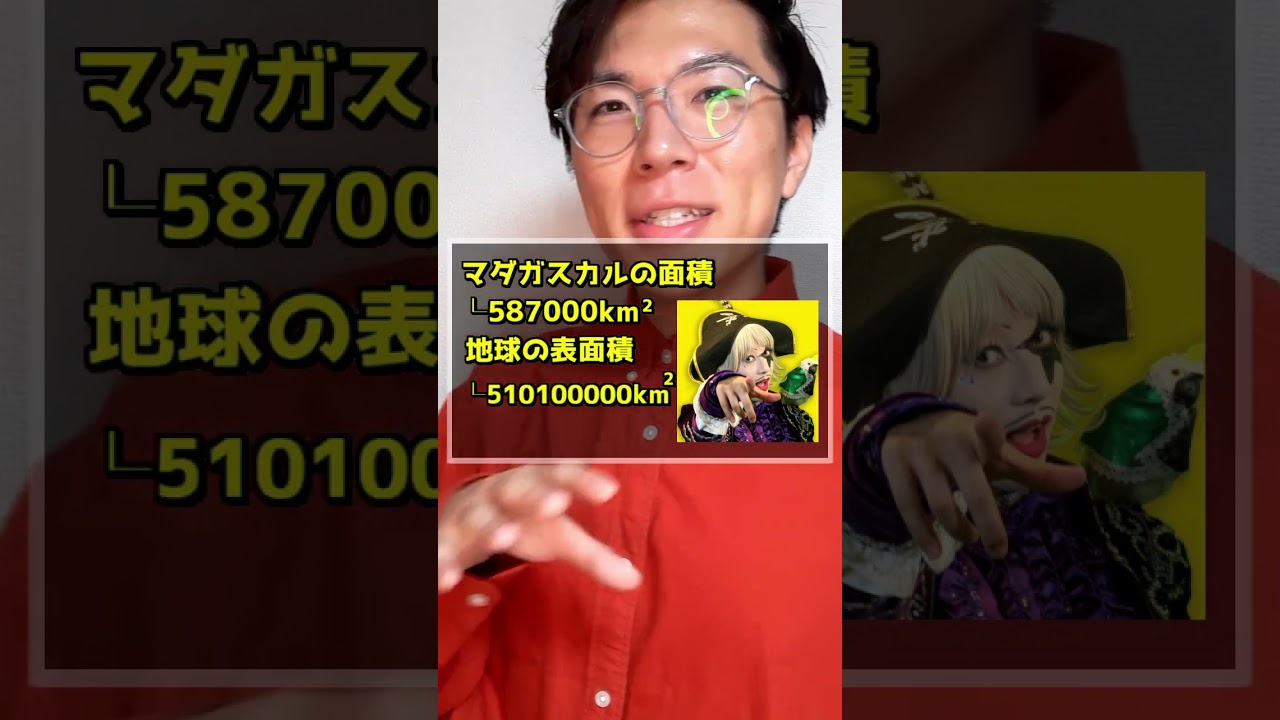
ここマダガスカルになる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
この動画を見る
下記質問の解説動画です
ここ!マダガスカルってやって当たる確率は?
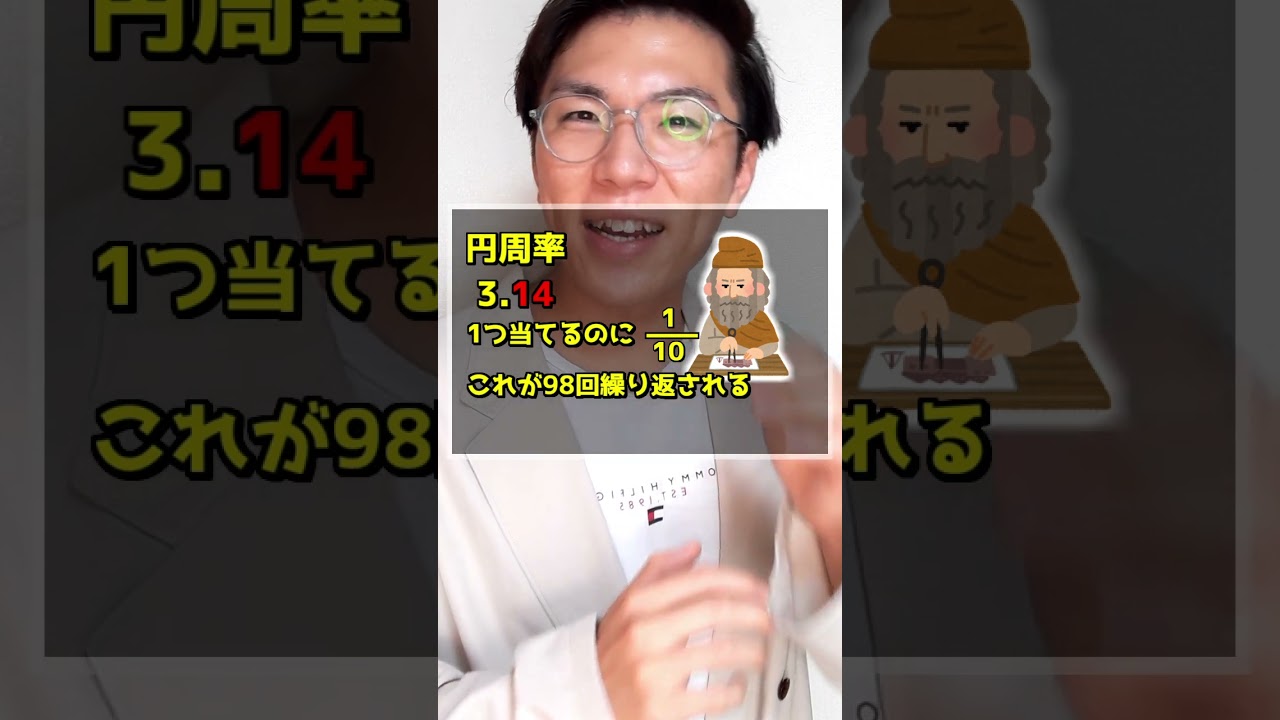
円周率100桁適当に当たる確率は?
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
この動画を見る
下記質問の解説動画です
適当に数字言って円周率100桁当たる確率は?
大人の階段が実際にあったら何段?

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
大人の階段が実際にあったら何段ですか?
この動画を見る
下記質問の解説動画です
大人の階段が実際にあったら何段ですか?
女優に数学教えてみた

ピカチュウ何匹で日本の電気まかなえる?

5億年ボタンの体感は?

空島の気温ってどれくらい?

関数って結局なんなん?

関数って結局なんなん?

単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数についての動画です。
例にとっているのは比例ですが,一次関数,二次関数,三次関数になっても考え方は同じです。
この動画を見る
関数についての動画です。
例にとっているのは比例ですが,一次関数,二次関数,三次関数になっても考え方は同じです。
ひろゆきが1年間にまばたきする回数は?

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ひろゆきは1年でどれくらいまばたきをしていますか?
この動画を見る
下記質問の解説動画です
ひろゆきは1年でどれくらいまばたきをしていますか?
サンジの鼻血の量がえぐかった

【高校物理】自由落下~公式覚えるな!!~ 1-5【物理基礎】

【高校物理】自由落下~公式覚えるな!!~ 1-5【物理基礎】

単元:
#物理#力学#理科(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
自由落下の基本的な授業動画です。
自由落下とは何か?を理解すれば公式は簡単に導けます。
大切なのはやはり,等加速度運動です。
パパっと覚えましょう
この動画を見る
自由落下の基本的な授業動画です。
自由落下とは何か?を理解すれば公式は簡単に導けます。
大切なのはやはり,等加速度運動です。
パパっと覚えましょう
3単現のsの覚え方~先生ととんとんの違い~

青キジが自転車で地球1周するのにかかる時間は?

何してるか分かる??
【保存版】学年底辺が1位になった勉強法

【保存版】学年底辺が1位になった勉強法

以上未満の覚え方~とんとんと先生の教え方の違い~

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
以上未満の覚え方
この動画を見る
以上未満の覚え方
【保存版】2次関数上の直線の式を一瞬で出す方法

デスノートで人類滅亡するには?

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
デスノートで人類滅亡させるのにどれくらいかかりますか?
この動画を見る
下記質問の解説動画です
デスノートで人類滅亡させるのにどれくらいかかりますか?
肩ぶつかって骨折れるときの速度は?
【高校物理】鉛直投げ下げの公式【物理基礎】

【高校物理】鉛直投げ下げの公式【物理基礎】

単元:
#物理#力学#理科(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
鉛直投げ下げ、鉛直投げ下ろしの動画です。
公式が新しく与えられているようで新しくはないので、簡単です。
ぜひ、使いこなせるようになってね。
この動画を見る
鉛直投げ下げ、鉛直投げ下ろしの動画です。
公式が新しく与えられているようで新しくはないので、簡単です。
ぜひ、使いこなせるようになってね。
2次関数のの裏技

橋本環奈と電話がつながるのにかかる時間は?

電卓のeの意味は!?





