 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
 【楽しい授業動画】あきとんとん
【楽しい授業動画】あきとんとん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【中学数学】点Pの1次関数の問題演習~解き方を身に付けろ~ 3-7【中2数学】

単元:
#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図のような長方形$ABCD$がある。点$P$は点$A$を出発し、毎秒$1\,\rm{cm}$の速さで長方形の周上を$A$から$D$まで移動する。
このとき、点$P$が点$A$を出発して$x$秒後の$\triangle APD$の面積を$y\,\rm{cm}^2$とする。
(1)点$P$が次の辺にあるとき$x$の変域を答えよ
①辺$AB$ ②辺$BC$ ③辺$CD$
(2)$x$が点$A$を出発してから点$D$に着くまでの$x$と$y$の関係をグラフに表せ
この動画を見る
図のような長方形$ABCD$がある。点$P$は点$A$を出発し、毎秒$1\,\rm{cm}$の速さで長方形の周上を$A$から$D$まで移動する。
このとき、点$P$が点$A$を出発して$x$秒後の$\triangle APD$の面積を$y\,\rm{cm}^2$とする。
(1)点$P$が次の辺にあるとき$x$の変域を答えよ
①辺$AB$ ②辺$BC$ ③辺$CD$
(2)$x$が点$A$を出発してから点$D$に着くまでの$x$と$y$の関係をグラフに表せ
周の長さ求めよ!小学生でもできるで
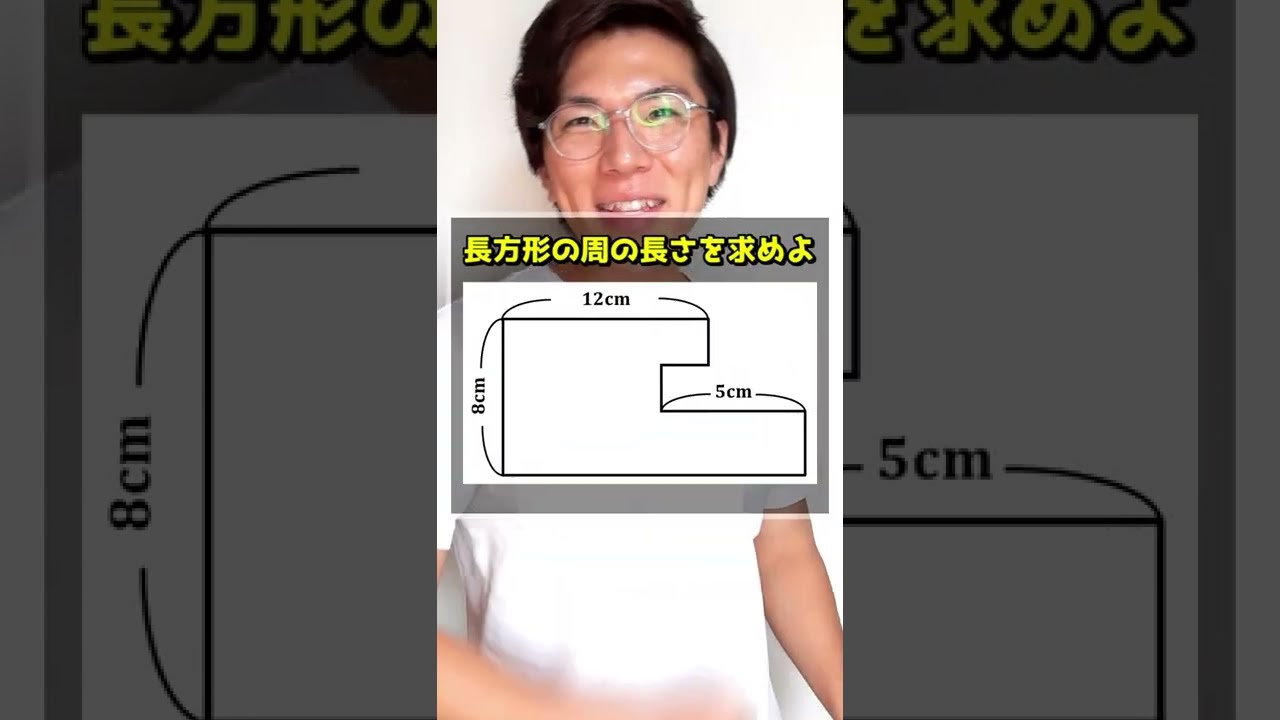
周の長さを求めよ!~小学生でも解けるで~
1円作るだけでどれだけ損してきたのか?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
お金作るのにそれ以上のお金使うって言いますが、日本はどれくらい損していますか?
この動画を見る
下記質問の解説動画です
お金作るのにそれ以上のお金使うって言いますが、日本はどれくらい損していますか?
キューピーは合計何分クッキング?

マークシート適当で満点の確率は?

【高校物理】等加速度運動の公式を理解させます~3つ目の公式~ 1-3【物理基礎】

これ分かる?

深読みしすぎた計算シリーズまとめ2

コロナ禍でマスクに何円使いましたか?

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
コロナ禍でマスクに何円使いましたか?
この動画を見る
下記質問の解説動画です
コロナ禍でマスクに何円使いましたか?
【正答率5%!?】平方根の計算できる?

単元:
#数学(中学生)#中3数学#平方根
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $\sqrt{{(1-\sqrt{2})}^2}$
(2) $\sqrt{{(3-\pi)}^2}$
この動画を見る
(1) $\sqrt{{(1-\sqrt{2})}^2}$
(2) $\sqrt{{(3-\pi)}^2}$
この解説できる?

単元:
#算数(中学受験)#平面図形#図形の移動
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2枚の100円。1枚の100円玉にピッタリもう一枚の100円玉をくっつけて回転させると何回転する?
この動画を見る
2枚の100円。1枚の100円玉にピッタリもう一枚の100円玉をくっつけて回転させると何回転する?
マジシャンって数学者よね?
100円の円周上を100円は何回転するのか?~どこよりも分かりやすい解説~

黄猿が50m走走ったらどうなる?

【高校物理】等加速度運動の公式を理解させます~位置の公式~ 1-2【物理基礎】

【高校物理】等加速度運動の公式を理解させます~位置の公式~ 1-2【物理基礎】

カルピスウォーターと原液どっちが得?

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
カルピスウォーターとカルピス原液のどっちがお得ですか?
この動画を見る
下記質問の解説動画です
カルピスウォーターとカルピス原液のどっちがお得ですか?
広告に何時間無駄にしているのか?

溶質と溶媒の教え方の違い~先生ととんとん~

【中学数学】2次関数の基礎を丁寧に~これは知らないとヤバい~ 4-1【中3数学】

これ分かる?平方根禁止

白ひげの息の温度計算したらヤバかった...

単元:
#物理#熱・波・音#理科(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
頂上戦争のときに白ひげが一吹きでマグマ冷ましてるんですが、実際どれくらいすごいんですか?
この動画を見る
下記質問の解説動画です
頂上戦争のときに白ひげが一吹きでマグマ冷ましてるんですが、実際どれくらいすごいんですか?
扇形の面積を求めよ!平方根は使用禁止です
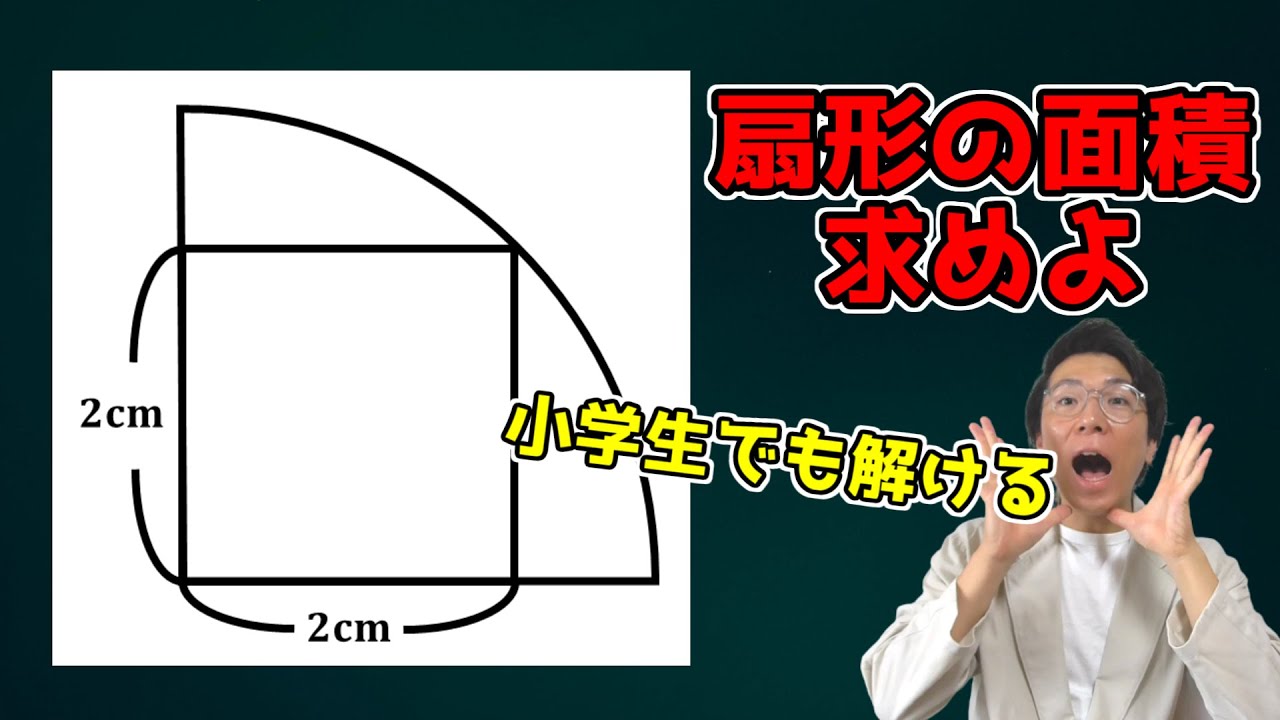
平方完成の裏技

3単現のs~あきとんとんと先生教え方の違い~

サウナで全身の水分なくなる回数は?

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
サウナ何回連続で入ったら身体中の水分なくなりますか?
この動画を見る
下記質問の解説動画です
サウナ何回連続で入ったら身体中の水分なくなりますか?
濱家さん食生活大丈夫そ??

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
かまいたちの濱家がYouTubeで、アメリカンドックを7万回食べたって言ってるんですけど、どうですか?
この動画を見る
下記質問の解説動画です
かまいたちの濱家がYouTubeで、アメリカンドックを7万回食べたって言ってるんですけど、どうですか?
『log』の解説を30秒でします

『√』平方根ルートの記号を誰でも理解させます





