福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の一夜漬け数学〜多変数関数１文字固定(3)〜受験編
単元：
#数Ⅱ#図形と方程式#指数関数と対数関数#微分法と積分法#軌跡と領域#指数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
三辺の長さがa,b,cである直方体を長さがbの一辺を回転軸として$90^{ \circ }$
回転させる。直方体が通過する点全体が作る体積をVとする。
(1)$V$を$a,b,c$で表せ。
(2)$a+b+c=1$のとき、$V$の取り得る値の範囲を求めよ。
この動画を見る
三辺の長さがa,b,cである直方体を長さがbの一辺を回転軸として$90^{ \circ }$
回転させる。直方体が通過する点全体が作る体積をVとする。
(1)$V$を$a,b,c$で表せ。
(2)$a+b+c=1$のとき、$V$の取り得る値の範囲を求めよ。
福田の一夜漬け数学〜多変数関数、１文字固定その２（受験編）
単元：
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
この動画を見る
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
福田の一夜漬け数学〜多変数関数、１文字固定（受験編）
単元：
#数Ⅱ#式と証明#図形と方程式#微分法と積分法#恒等式・等式・不等式の証明#軌跡と領域#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a+b+c=1$のとき、$a^2+b^2+c^2$の最小値を求めよ。
$xy$平面内の領域$-1 \leqq x \leqq 1,-1 \leqq y \leqq 1$ において、$1-ax-by+axy$
の最小値が正であるような$(a,b)$の存在範囲を図示せよ。
この動画を見る
$a+b+c=1$のとき、$a^2+b^2+c^2$の最小値を求めよ。
$xy$平面内の領域$-1 \leqq x \leqq 1,-1 \leqq y \leqq 1$ において、$1-ax-by+axy$
の最小値が正であるような$(a,b)$の存在範囲を図示せよ。
福田の一夜漬け数学〜複素数平面(1)〜極形式と回転
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
(練習)以下の式を極形式表示に直せ。ただし$0 \leqq \theta\leqq 2\pi$とする。
(1)$2-2i$
(2)$(2-2\sqrt3i)(i-1)$
$\alpha=1+i,\beta=3+2i$のとき、この2点を一辺とする正三角形の
残りの頂点を表す複素数を求めよ。
この動画を見る
(練習)以下の式を極形式表示に直せ。ただし$0 \leqq \theta\leqq 2\pi$とする。
(1)$2-2i$
(2)$(2-2\sqrt3i)(i-1)$
$\alpha=1+i,\beta=3+2i$のとき、この2点を一辺とする正三角形の
残りの頂点を表す複素数を求めよ。
福田の一夜漬け数学〜ルート計算のコツ(2)値の計算
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x=\frac{\sqrt5+2}{\sqrt5-2}$
$y=\frac{\sqrt5-2}{\sqrt5+2}$ のとき、次の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3$
(5)$x^4+y^4$
(6)$x^5+y^5$
$x=\sqrt5+2$のとき、次の値を求めよ。
(1)$x+\frac{1}{x}$
(2)$x^2+\frac{1}{x^2}$
(3)$x^3+\frac{1}{x^3}$
(4)$x^4+\frac{1}{x^4}$
(5)$x^5+\frac{1}{x^5}$
$\frac{1}{2-\sqrt3}$の整数部分を$a$,少数部分を$b$とする。次の値を求めよ。
(1)$a$
(2)$b$
(3)$a+b+b^2$
この動画を見る
$x=\frac{\sqrt5+2}{\sqrt5-2}$
$y=\frac{\sqrt5-2}{\sqrt5+2}$ のとき、次の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3$
(5)$x^4+y^4$
(6)$x^5+y^5$
$x=\sqrt5+2$のとき、次の値を求めよ。
(1)$x+\frac{1}{x}$
(2)$x^2+\frac{1}{x^2}$
(3)$x^3+\frac{1}{x^3}$
(4)$x^4+\frac{1}{x^4}$
(5)$x^5+\frac{1}{x^5}$
$\frac{1}{2-\sqrt3}$の整数部分を$a$,少数部分を$b$とする。次の値を求めよ。
(1)$a$
(2)$b$
(3)$a+b+b^2$
福田の一夜漬け数学〜ルート計算のコツ(1)〜有理化と二重根号
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
次の分数を有理化せよ。
$\frac{\sqrt2+\sqrt3-\sqrt5}{\sqrt2-\sqrt3+\sqrt5}$
$\frac{\sqrt2+\sqrt5+\sqrt7}{\sqrt2+\sqrt5-\sqrt7}+\frac{\sqrt2-\sqrt5+\sqrt7}{\sqrt2-\sqrt5-\sqrt7}$
以下の2重根号を外し、最も簡単な数で表せ。
$\sqrt{4+2\sqrt3}$
$\sqrt{5-2\sqrt6}$
$\sqrt{5+\sqrt{24}}$
$\sqrt{4+\sqrt7}$
$\sqrt{10+5\sqrt3}$
この動画を見る
次の分数を有理化せよ。
$\frac{\sqrt2+\sqrt3-\sqrt5}{\sqrt2-\sqrt3+\sqrt5}$
$\frac{\sqrt2+\sqrt5+\sqrt7}{\sqrt2+\sqrt5-\sqrt7}+\frac{\sqrt2-\sqrt5+\sqrt7}{\sqrt2-\sqrt5-\sqrt7}$
以下の2重根号を外し、最も簡単な数で表せ。
$\sqrt{4+2\sqrt3}$
$\sqrt{5-2\sqrt6}$
$\sqrt{5+\sqrt{24}}$
$\sqrt{4+\sqrt7}$
$\sqrt{10+5\sqrt3}$
福田の一夜漬け数学〜平面ベクトル(1)〜受験編・文理共通
単元：
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$k$を正の実数とする。点Pは$\triangle ABC$の内部にあり、
$k\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }\\$
を満たしている。また、辺$BC$を$3:5$に内分する点を$D$とする。
(1)$\overrightarrow{ AP }$を、$\overrightarrow{ AB },\overrightarrow{ AC },k$を用いて表せ。
(2)3点$A,P,D$は一直線上にあることを示せ。
(3)$\triangle ABP$の面積が$\triangle CDP$の面積の$\frac{6}{5}$倍に等しいとき
$k$の値を求めよ。
【もとになる問題】
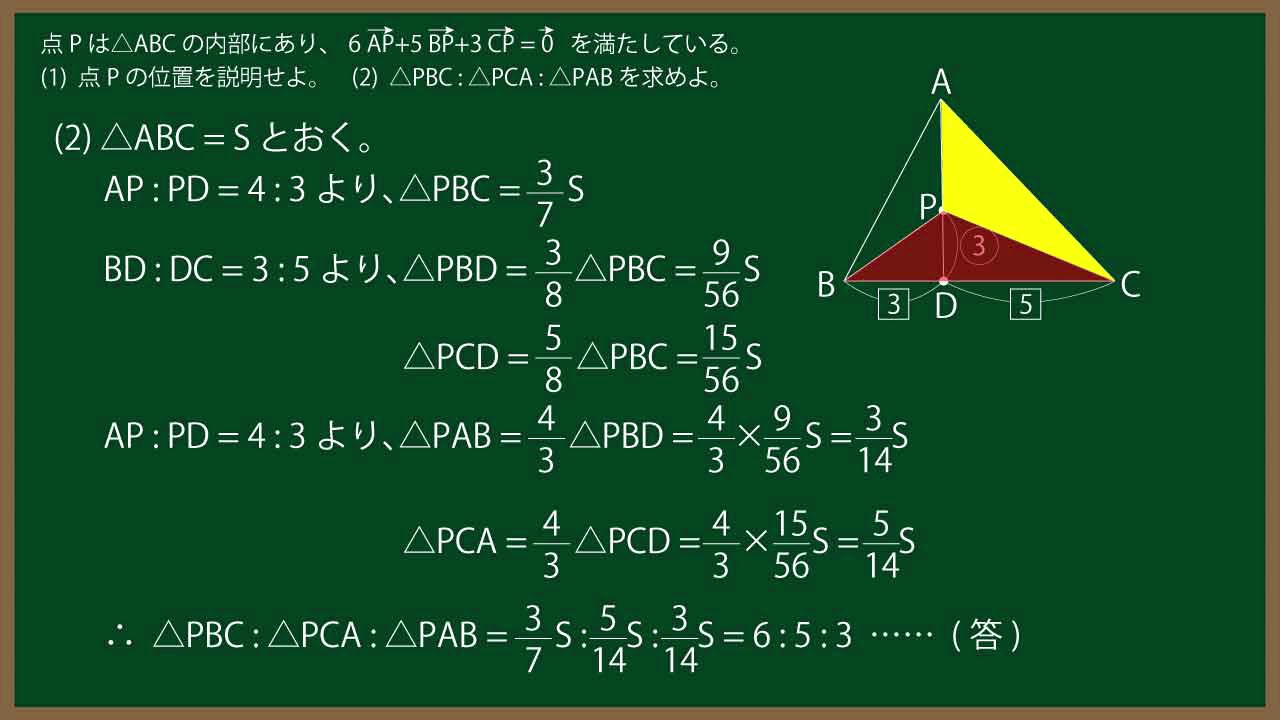
点$P$は$\triangle ABC$の内部にあり、
$6\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たしている。
(1)点$P$の位置を説明せよ。
(2)$\triangle PBC:\triangle PCA:\triangle PAB$を求めよ。
この動画を見る
$k$を正の実数とする。点Pは$\triangle ABC$の内部にあり、
$k\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }\\$
を満たしている。また、辺$BC$を$3:5$に内分する点を$D$とする。
(1)$\overrightarrow{ AP }$を、$\overrightarrow{ AB },\overrightarrow{ AC },k$を用いて表せ。
(2)3点$A,P,D$は一直線上にあることを示せ。
(3)$\triangle ABP$の面積が$\triangle CDP$の面積の$\frac{6}{5}$倍に等しいとき
$k$の値を求めよ。
【もとになる問題】
点$P$は$\triangle ABC$の内部にあり、
$6\ \overrightarrow{ AP }+5\ \overrightarrow{ BP }+3\ \overrightarrow{ CP }=\overrightarrow{ 0 }$
を満たしている。
(1)点$P$の位置を説明せよ。
(2)$\triangle PBC:\triangle PCA:\triangle PAB$を求めよ。
福田の一夜漬け数学〜因数分解たすきがけのコツ
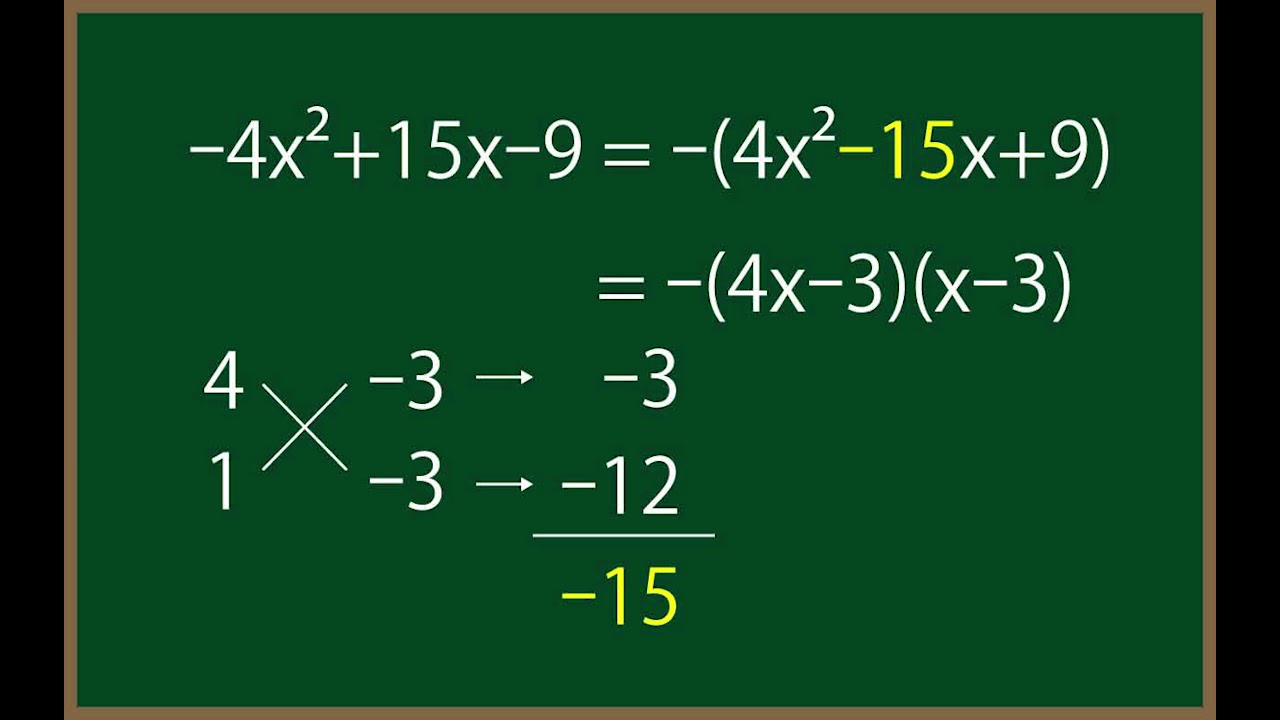
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
以下の式をたすき掛けを用いて因数分解せよ。
$4x^2+8x-21$
$12x^2-10x-12$
$-4x^2+15x-9$
$3x^2-2xy-y^2$
$2x^2+5xy+3y^2-3x-5y-2$
$a(b^2-c^2)$$+b(c^2-a^2)$$+c(a^2-b^2)$
この動画を見る
以下の式をたすき掛けを用いて因数分解せよ。
$4x^2+8x-21$
$12x^2-10x-12$
$-4x^2+15x-9$
$3x^2-2xy-y^2$
$2x^2+5xy+3y^2-3x-5y-2$
$a(b^2-c^2)$$+b(c^2-a^2)$$+c(a^2-b^2)$