ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#481「個人的には複雑な7手詰め【5分で2段】」 明治大学(2022) #定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\theta}{(1+\cos\theta)^2} d\theta$
出典：2022年明治大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\theta}{(1+\cos\theta)^2} d\theta$
出典：2022年明治大学 入試問題
大学入試問題#480「計算量が多いのかもしれません」 山形大学(2016) #微積の応用②
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$微分可能な関数
$e^{-x}f(x)+\displaystyle \int_{0}^{x} e^{-t}f(t)dt=1+e^{-2x}(3\ \sin\ x-\cos\ x)$を満たす$f(x)$を求めよ
出典：2016年山形大学 入試問題
この動画を見る
$f(x)$微分可能な関数
$e^{-x}f(x)+\displaystyle \int_{0}^{x} e^{-t}f(t)dt=1+e^{-2x}(3\ \sin\ x-\cos\ x)$を満たす$f(x)$を求めよ
出典：2016年山形大学 入試問題
大学入試問題#479「教科書で紹介されてそう」 山形大学(2016) 微積の応用①
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\sin^2x+2\displaystyle \int_{0}^{\frac{\pi}{2}} f(t)\cos\ t\ dx$を満たす$f(x)$を求めよ。
出典：2016年山形大学 入試問題
この動画を見る
$f(x)=\sin^2x+2\displaystyle \int_{0}^{\frac{\pi}{2}} f(t)\cos\ t\ dx$を満たす$f(x)$を求めよ。
出典：2016年山形大学 入試問題
大学入試問題#477「よくある極限の問題」 藤田医科大学(2023) #極限
単元：
#関数と極限#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(e^x-1)log(4x+1)}{x^2}$
出典：2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(e^x-1)log(4x+1)}{x^2}$
出典：2023年藤田医科大学 入試問題
大学入試問題#478「これは落とせない問題でしょう。」 福島大学(2022) #方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典：2022年福島大学 入試問題
この動画を見る
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典：2022年福島大学 入試問題
大学入試問題#477「もうすこし工夫できそう」 山形大学(2016) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ#大阪市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{1}{e}}^{1} (1+\displaystyle \frac{1}{x})log\ x\ dx$
出典：2016年山形大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{1}{e}}^{1} (1+\displaystyle \frac{1}{x})log\ x\ dx$
出典：2016年山形大学 入試問題
大学入試問題#476「むむむ！」 信州大学(2010) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典：2010年信州大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典：2010年信州大学 入試問題
大学入試問題#475「エフ(f)３つ！」 早稲田大学(2004) #逆関数
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
実数$a$に対して
$f(x)=ax+2$とする
$f(f(f(x)))$が$f(x)$の逆関数になるような$a$の値を求めよ。
出典：2004年早稲田大学理工 入試問題
この動画を見る
実数$a$に対して
$f(x)=ax+2$とする
$f(f(f(x)))$が$f(x)$の逆関数になるような$a$の値を求めよ。
出典：2004年早稲田大学理工 入試問題
大学入試問題#474「沼にはまりがち」 信州大学後期(2011) #不定積分
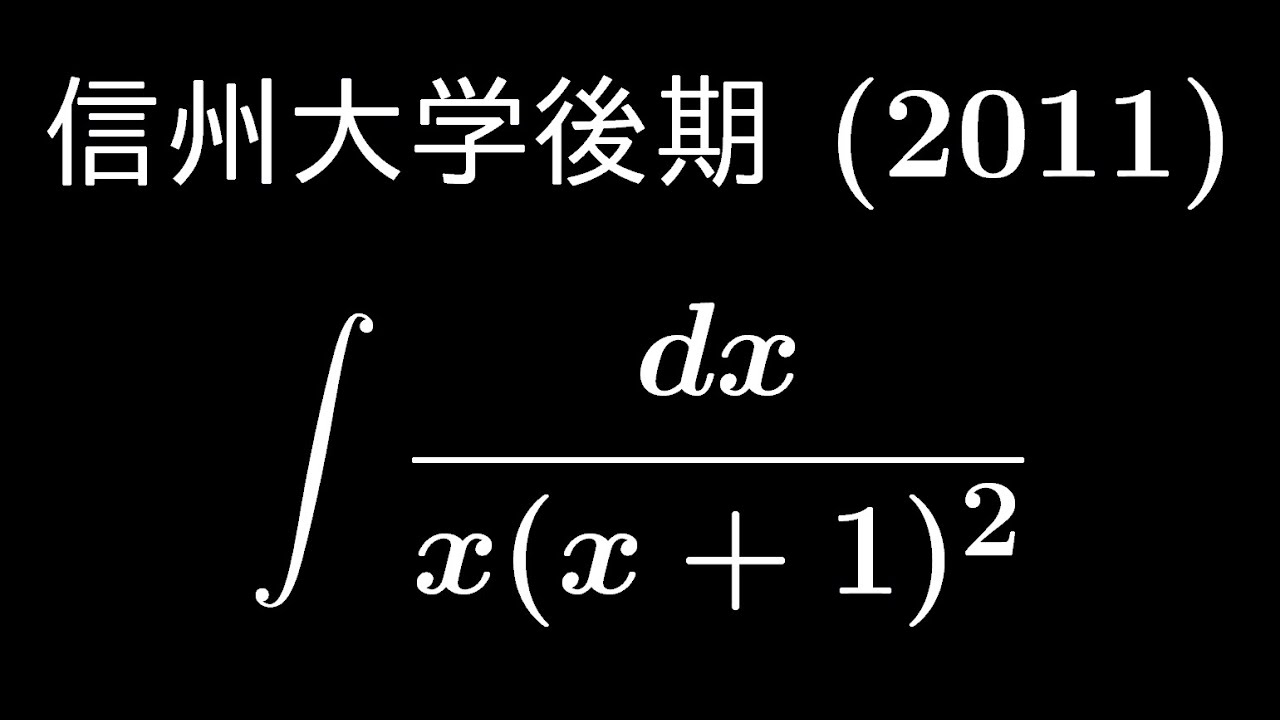
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典：2011年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典：2011年信州大学後期 入試問題
大学入試問題#473「計算は大変かもしれない」 信州大学 理・医 (2011) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典：2011年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典：2011年信州大学 入試問題
大学入試問題#472「最後の計算量を減らすには？」 弘前大学(2012) #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{e^{4x}}{e^x+1} dx$
出典：2012年弘前大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{4x}}{e^x+1} dx$
出典：2012年弘前大学 入試問題
大学入試問題#471「深夜1時でストック０」 信州大学後期(2013) 不定積分
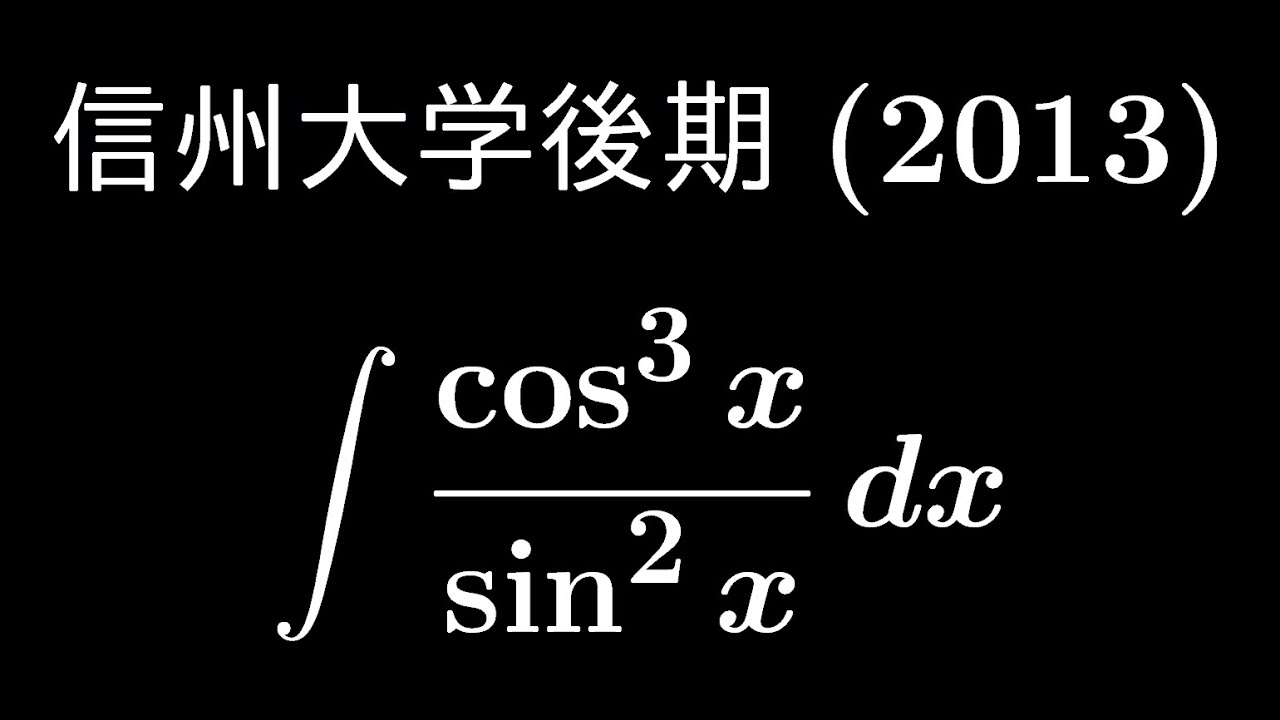
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2013年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典：2013年信州大学後期 入試問題
大学入試問題#470「誘導なくてもどうにかできそう」 信州大学 理・医学部(2021) #微積の応用
単元：
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
（1）
$f(0)$を求めよ
（2）
$f(x)$は微分可能を示せ
$f(x)$を求めよ
（3）
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典：2021年信州大学 入試問題
この動画を見る
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
（1）
$f(0)$を求めよ
（2）
$f(x)$は微分可能を示せ
$f(x)$を求めよ
（3）
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典：2021年信州大学 入試問題
大学入試問題#469「なんかワクワクする積分」 千葉大学2011 #定積分
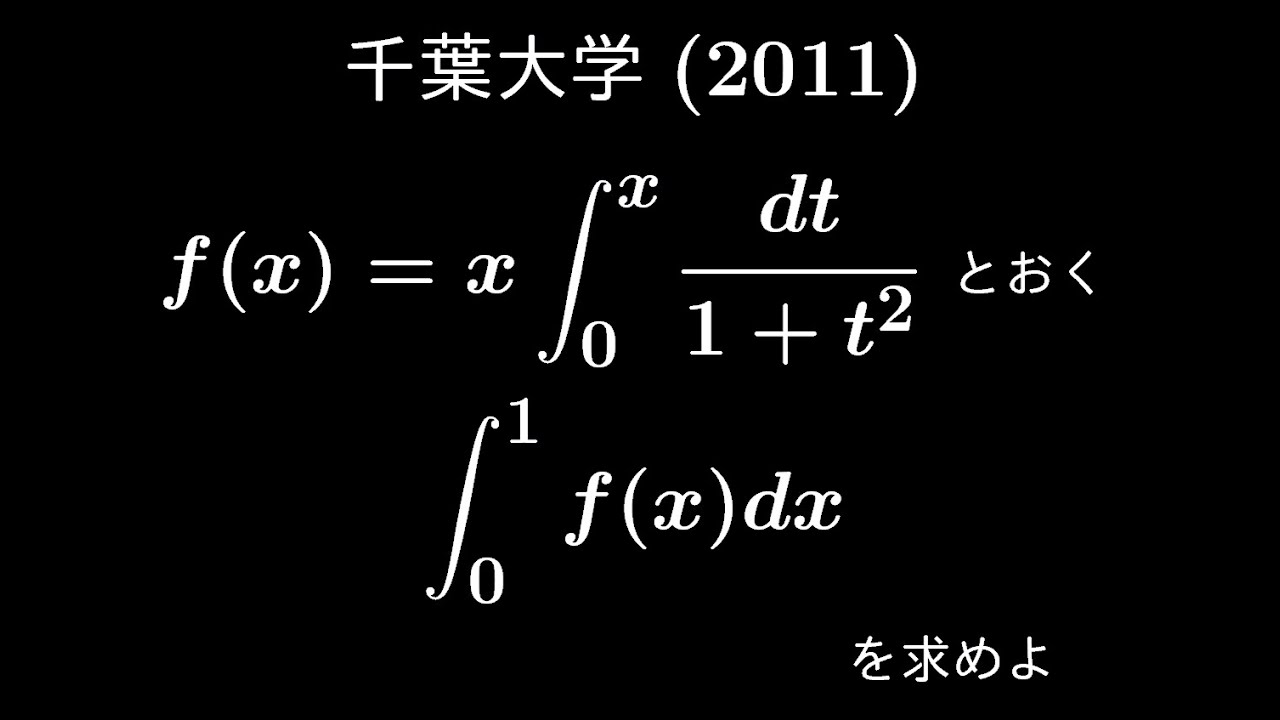
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x\displaystyle \int_{0}^{x} \displaystyle \frac{dt}{1+t^2}$とおく
$\displaystyle \int_{0}^{1} f(x) dx$を求めよ
出典：2011年千葉大学 入試問題
この動画を見る
$f(x)=x\displaystyle \int_{0}^{x} \displaystyle \frac{dt}{1+t^2}$とおく
$\displaystyle \int_{0}^{1} f(x) dx$を求めよ
出典：2011年千葉大学 入試問題
大学入試問題#468「パズルで遊ぶ感じ」 岩手大学(2022) 微積の応用
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$：微分可能
$g(x)=f(x)e^{-x}$
（1）
$f'(x)=f(x)+g'(x)e^x$を示せ
（2）
$a$：定数
$f(x)=\displaystyle \int_{a}^{x} (f(t)-4te^{-t}) dt$
$f(0)=1$のとき$f(x),a$を求めよ
出典：2022年岩手大学 入試問題
この動画を見る
$f(x)$：微分可能
$g(x)=f(x)e^{-x}$
（1）
$f'(x)=f(x)+g'(x)e^x$を示せ
（2）
$a$：定数
$f(x)=\displaystyle \int_{a}^{x} (f(t)-4te^{-t}) dt$
$f(0)=1$のとき$f(x),a$を求めよ
出典：2022年岩手大学 入試問題
大学入試問題#467「基本すぎる極限問題」 電気通信大学(2013) #極限
単元：
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典：2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典：2013年電気通信大学 入試問題
大学入試問題#466「絶対に知っておくべき解き方」 電気通信大学(2014) #極限
単元：
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典：2014年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典：2014年電気通信大学 入試問題
大学入試問題#465「よくある極限問題」 電気通信大学2009 #極限
単元：
#大学入試過去問(数学)#三角関数#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典：2009年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典：2009年電気通信大学 入試問題
大学入試問題#464「誘導の力は偉大」 神戸大学(2000) #不定積分 #積分の応用
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \frac{1}{x^3(1-x)}$
（1）
$f(x)=\displaystyle \frac{a_1}{x}+\displaystyle \frac{a_2}{x^2}+\displaystyle \frac{a_3}{x^3}+\displaystyle \frac{b}{1-x}$
とおくとき、定数$a_1,a_2,a_3,b$を求めよ
（2）
$\displaystyle \int f(x) dx$
（3）
$\displaystyle \int \displaystyle \frac{dx}{x^P(1-x)}(P=1,2,3,・・・)$
出典：2000年神戸大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{1}{x^3(1-x)}$
（1）
$f(x)=\displaystyle \frac{a_1}{x}+\displaystyle \frac{a_2}{x^2}+\displaystyle \frac{a_3}{x^3}+\displaystyle \frac{b}{1-x}$
とおくとき、定数$a_1,a_2,a_3,b$を求めよ
（2）
$\displaystyle \int f(x) dx$
（3）
$\displaystyle \int \displaystyle \frac{dx}{x^P(1-x)}(P=1,2,3,・・・)$
出典：2000年神戸大学 入試問題
大学入試問題#463「ええ問題や～～」 信州大学 理・医 (2016) #積分の応用
単元：
#大学入試過去問(数学)#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典：2016年信州大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典：2016年信州大学医学部 入試問題
数検1級1次過去問 #微分方程式
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$y(0)=1,\ y'(0)=5$
$y''-6y'+9y=6e^{3x}$を満たす微分方程式の解を求めよ。
出典：数字検定1級1次
この動画を見る
$y(0)=1,\ y'(0)=5$
$y''-6y'+9y=6e^{3x}$を満たす微分方程式の解を求めよ。
出典：数字検定1級1次
大学入試問題#462「~らん~さんからの紹介」 横国・信州大学 類題 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{e^x+e^{-x}}{e^{(\sin^5x+1)}+e} dx$
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{e^x+e^{-x}}{e^{(\sin^5x+1)}+e} dx$
大学入試問題「明日の2次試験にでる問題」 ハルハルさんの名作（過去1番） 体感偏差値は72
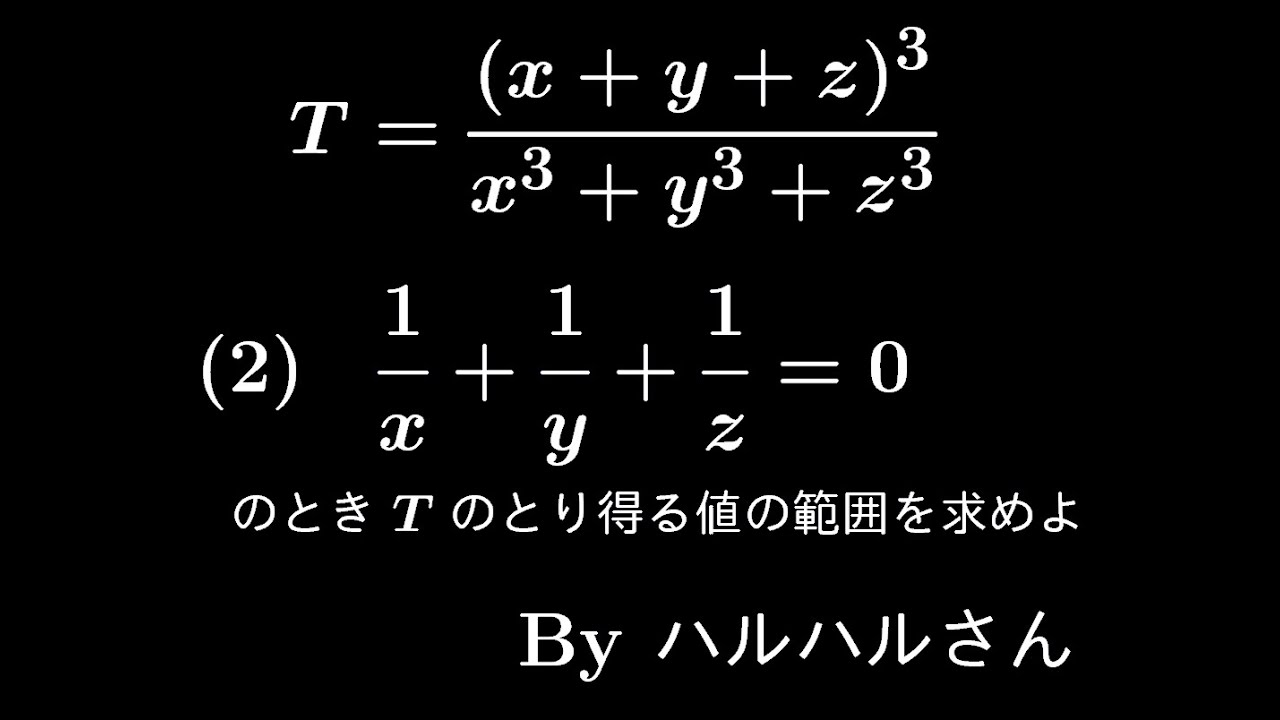
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$T=\displaystyle \frac{(x+y+z)^3}{x^3+y^3+z^3}$
$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{y}+\displaystyle \frac{1}{z}=0$のとき
$T$のとりうる値の範囲を求めよ
この動画を見る
$T=\displaystyle \frac{(x+y+z)^3}{x^3+y^3+z^3}$
$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{y}+\displaystyle \frac{1}{z}=0$のとき
$T$のとりうる値の範囲を求めよ
大学入試問題#461「どう処理すべきか」 関西大学(2009) #不定積分
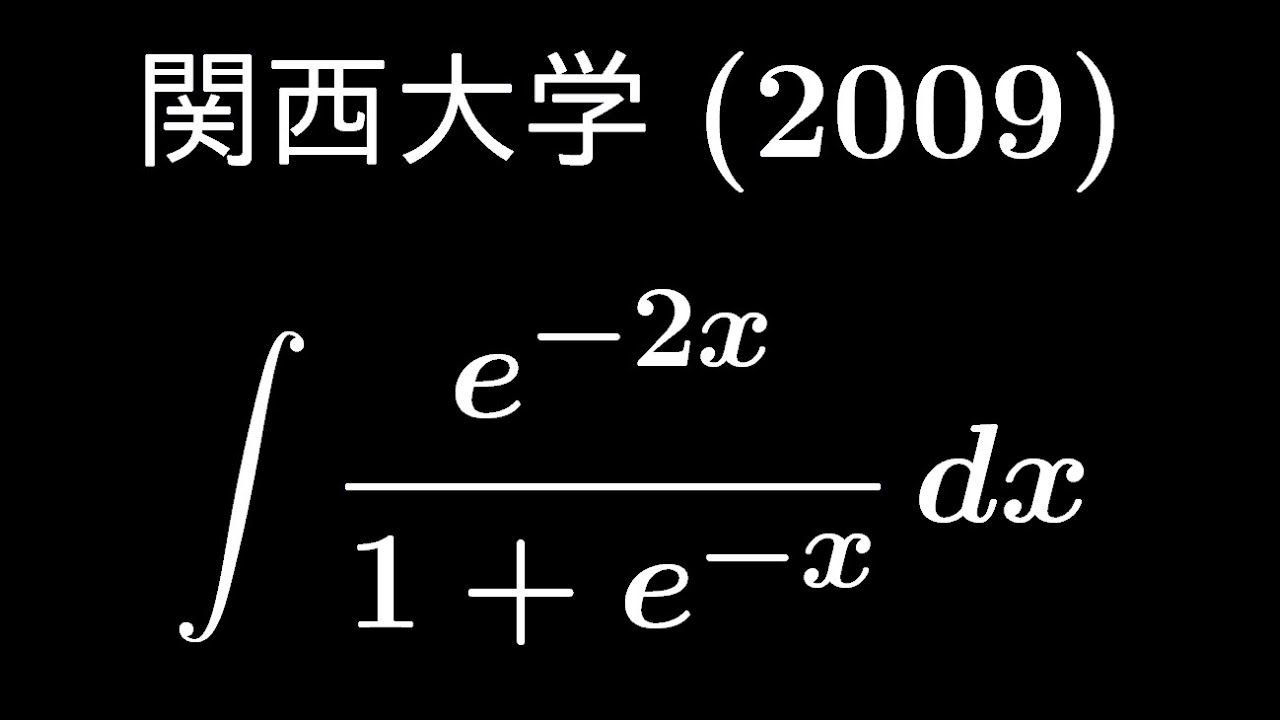
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{e^{-2x}}{1+e^{-x}} dx$
出典：2009年関西大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{-2x}}{1+e^{-x}} dx$
出典：2009年関西大学 入試問題
大学入試数学#460「基本に寄り添って」 横浜国立大学(2000) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^32^{x^2}\ dx$
出典：2000年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^32^{x^2}\ dx$
出典：2000年横浜国立大学 入試問題
大学入試問題#459「構想力が問われる問題」 早稲田大学(2017) #連続関数
単元：
#大学入試過去問(数学)#関数と極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$C$：定数 $-1 \lt C \lt 1$
すべての実数$x$に対して
$f(x)+f(cx)=x^2$を満たす連続関数$f(x)$を求めよ
出典：2017年早稲田大学 入試問題
この動画を見る
$C$：定数 $-1 \lt C \lt 1$
すべての実数$x$に対して
$f(x)+f(cx)=x^2$を満たす連続関数$f(x)$を求めよ
出典：2017年早稲田大学 入試問題
大学入試問題#458「これはさすがに落とせない！」 横浜国立大学(2000) #定積分
単元：
#大学入試過去問(数学)#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典：2000年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{log\ x}{(1+x)^2} dx$
出典：2000年横浜国立大学 入試問題
大学入試問題#457「いかにしてサッパリ解くか！」 横浜国立大学(2001) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \displaystyle \frac{dx}{x\sqrt{ 1+x^3 }}$
出典：2001年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{dx}{x\sqrt{ 1+x^3 }}$
出典：2001年横浜国立大学 入試問題
大学入試問題#456「きれいな整数問題」 一橋大学(2009) #整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m^3+1^3=n^3+10^3$を満たす2以上の整数$m,n$の組（$m,n$）をすべて求めよ。
出典：2009年一橋大学 入試問題
この動画を見る
$m^3+1^3=n^3+10^3$を満たす2以上の整数$m,n$の組（$m,n$）をすべて求めよ。
出典：2009年一橋大学 入試問題
大学入試問題#455「落とすと落ちる問題② 横浜国立大学 後期 (2003) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{16} \displaystyle \frac{dx}{\sqrt{ x }+\sqrt[ 4 ]{ x }}$
出典：2003年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{16} \displaystyle \frac{dx}{\sqrt{ x }+\sqrt[ 4 ]{ x }}$
出典：2003年横浜国立大学 入試問題