ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#204 東京大学（改） 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{\sqrt{ 3 }}\sqrt{ 1+\displaystyle \frac{1}{x^2} }\ dx$
出典：東京大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }}\sqrt{ 1+\displaystyle \frac{1}{x^2} }\ dx$
出典：東京大学 入試問題
大学入試問題#203 琉球大学(2020) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典：2020年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{log2}^{log3}\displaystyle \frac{xe^x}{(e^x-1)^2}dx$を計算せよ
出典：2020年琉球大学 入試問題
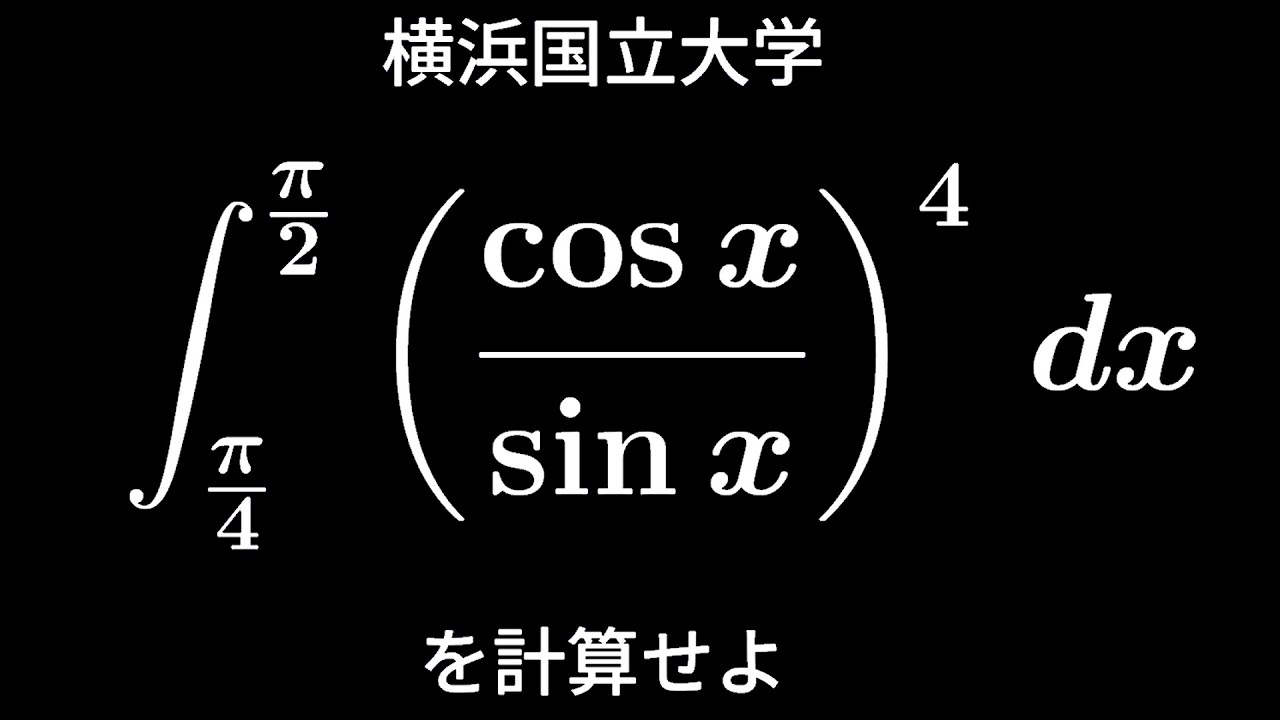
大学入試問題#202 横浜国立大学 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(\displaystyle \frac{\cos\ x}{\sin\ x})^4dx$
出典：横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{\pi}{2}}(\displaystyle \frac{\cos\ x}{\sin\ x})^4dx$
出典：横浜国立大学 入試問題
大学入試問題#201 山梨大学(2021) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\cos(\sin\ x)\sin2x\ dx$を計算せよ
出典：2021年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\cos(\sin\ x)\sin2x\ dx$を計算せよ
出典：2021年山梨大学 入試問題
大学入試問題#200 大阪教育大学2022 定積分 King property
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪教育大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{8+\sin^2x}\ dx$
出典：2022年大阪教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{8+\sin^2x}\ dx$
出典：2022年大阪教育大学 入試問題
大学入試問題#199 東京都市大学(2016) 定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^3-1}{x^2-1}\ dx$
出典：2016年東京都市大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3}\displaystyle \frac{x^3-1}{x^2-1}\ dx$
出典：2016年東京都市大学 入試問題
ハルハル様の作成問題② 複雑な方程式の解
大学入試問題#198 東京理科大学2010 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{2x+2}{x^2+x+1}\ dx$を計算せよ。
出典：2010年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{2x+2}{x^2+x+1}\ dx$を計算せよ。
出典：2010年東京理科大学 入試問題
大学入試問題#197 明治大学（改） 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{e^{2x}-1}{e^{2x}+1}\ dx$
出典：明治大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{e^{2x}-1}{e^{2x}+1}\ dx$
出典：明治大学 入試問題
大学入試問題#196 神戸薬科大学2020 定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2}\sqrt{ (x+1)^2-4x }\ dx$を計算せよ。
出典：2020年神戸薬科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2}\sqrt{ (x+1)^2-4x }\ dx$を計算せよ。
出典：2020年神戸薬科大学 入試問題
大学入試問題#195 兵庫医科大学 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#兵庫医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{0}\displaystyle \frac{x^5}{(x^3-1)}\ dx$を計算せよ。
出典：兵庫医科大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{0}\displaystyle \frac{x^5}{(x^3-1)}\ dx$を計算せよ。
出典：兵庫医科大学 入試問題
大学入試問題#194 横浜国立大学 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \sqrt{ 1-e^{-2x} }\ dx$を計算せよ。
出典：横浜国立大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ 1-e^{-2x} }\ dx$を計算せよ。
出典：横浜国立大学 入試問題
大学入試問題#193 東海大学医学部 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi}\ x\ \cos^2x\ \sin\ x\ dx$を求めよ。
出典：東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}\ x\ \cos^2x\ \sin\ x\ dx$を求めよ。
出典：東海大学医学部 入試問題
大学入試問題#192 東京大学(昭和9年) 不定積分 3手1組の好手順
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ 1+x^6 }}\ dx$を計算せよ。
出典：昭和9年東京大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ 1+x^6 }}\ dx$を計算せよ。
出典：昭和9年東京大学 入試問題
大学入試問題#191 岡山県立大学(2013) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{log(\cos\ x)}{\cos^2x}\ dx$
出典：2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{log(\cos\ x)}{\cos^2x}\ dx$
出典：2013年岡山県立大学 入試問題
大学入試問題#190 奈良県立医科大学(1987) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#奈良県立医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{x}{\sqrt{ 4-3x^2 }}\ dx$を計算せよ。
出典：1987年奈良県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x}{\sqrt{ 4-3x^2 }}\ dx$を計算せよ。
出典：1987年奈良県立医科大学 入試問題
大学入試問題#189 早稲田大学(2005) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典：2005年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典：2005年早稲田大学 入試問題
大学入試問題#188 会津大学(2021) 定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{1+log(log\ x)}{x}\ dx$を計算せよ。
出典：2021年会津大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{1+log(log\ x)}{x}\ dx$を計算せよ。
出典：2021年会津大学 入試問題
大学入試問題#187 慶應義塾大学(2006) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{e}^{e^e}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典：2006年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^e}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典：2006年慶應義塾大学 入試問題
大学入試問題#186 京都大学医学部(大正15年) 不定積分 たぶん難問
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典：大正15年京都大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典：大正15年京都大学医学部 入試問題
大学入試問題#185 大阪府立大学(2010) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{\sqrt{ (3+x^2)^3 }}dx$を計算せよ。
出典：2010年大阪府立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{\sqrt{ (3+x^2)^3 }}dx$を計算せよ。
出典：2010年大阪府立大学 入試問題
大学入試問題#184 早稲田大学 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典：早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典：早稲田大学 入試問題
大学入試問題#183 東京理科大学 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{2+3e^x+e^{2x}}$
出典：東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{2+3e^x+e^{2x}}$
出典：東京理科大学 入試問題
大学入試問題#182 横浜国立大学 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典：横浜国立大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典：横浜国立大学 入試問題
【誘導形式：概要欄】大学入試問題#181 九州大学改(1987) 定積分 ウォリス積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典：1987年九州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典：1987年九州大学 入試問題
大学入試問題#180 秋田県立大学(2004) 定積分 ウォリス積分②
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}(1-x^2)^4\ dx$
出典：2004年秋田県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}(1-x^2)^4\ dx$
出典：2004年秋田県立大学 入試問題
大学入試問題#179 秋田県立大学(2004) 定積分 ウォリス積分①
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}(1-x^2)^3 dx$
出典：2004年秋田県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}(1-x^2)^3 dx$
出典：2004年秋田県立大学 入試問題
大学入試問題#178 東京大学昭和10年 定積分 King property
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{1+\cos^2x}\ dx$を計算せよ。
出典：昭和10年東京大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}\displaystyle \frac{x\ \sin\ x}{1+\cos^2x}\ dx$を計算せよ。
出典：昭和10年東京大学 入試問題
大学入試問題#177 東京都市大学(2017) 定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }}\ dx$
出典：2017年東京都市大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }}\ dx$
出典：2017年東京都市大学 入試問題
大学入試問題#176 日本医科大学(2019) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典：2019年日本医科大学 入試問題
この動画を見る
$\displaystyle \int \sqrt{ x^2+1 }\ dx$
出典：2019年日本医科大学 入試問題