 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【学部紹介】独断と偏見に基づく学部紹介文学部編その2(心理学紹介)

【学部紹介】独断と偏見に基づく学部紹介文学部編その1

【受験算数】平面図形:葉っぱ型の面積を一瞬で解く!

【受験算数】平面図形:星形の角度の和を求めよう!

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
理数個別チャンネル
問題文全文(内容文):
星形の角度の和を求める問題です。一つひとつは出せないけども・・・、まとめてなら出せます。
この動画を見る
星形の角度の和を求める問題です。一つひとつは出せないけども・・・、まとめてなら出せます。
【数Ⅲ】極限:数列の極限と関数の極限の違いを解説します

【英語】医学部受験生なら全問正解で当たり前の英単語テスト -超基本-

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#名詞・冠詞・代名詞#勉強法・その他#勉強法#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
医学部に興味があったり、医学部を目指す生徒必見!医学部の英単語についての動画です。
この動画を見る
医学部に興味があったり、医学部を目指す生徒必見!医学部の英単語についての動画です。
【受験理科】天体:地球と月の位置から見える月の形を求めます

【英語】医学部受験生なら全問正解で当たり前の英単語テスト -超基本-

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
【英語】医学部受験生なら全問正解で当たり前の英単語テスト -超基本-解説してみた.
この動画を見る
【英語】医学部受験生なら全問正解で当たり前の英単語テスト -超基本-解説してみた.
【英語語彙】includeとcontainの違い!

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
includeとcontainの区別について基礎から丁寧に解説します。用法や実際の使い方も紹介!
この動画を見る
includeとcontainの区別について基礎から丁寧に解説します。用法や実際の使い方も紹介!
【受験算数】高さ3.7mの街灯から6m離れたところに、高さ3m、はば5mの長方形 のへいが地面に垂直に立っています。(1)PBの長さは何mですか。 (2)地面にできたへいの影の面積は何m²ですか

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図のように、高さ3.7mの街灯から6m離れたところに、高さ3m、はば5mの長方形 のへいが地面に垂直に立っています。次の問に答えよ。
(1)PBの長さは何mですか。 (2)地面にできたへいの影の面積は何m²ですか
この動画を見る
右図のように、高さ3.7mの街灯から6m離れたところに、高さ3m、はば5mの長方形 のへいが地面に垂直に立っています。次の問に答えよ。
(1)PBの長さは何mですか。 (2)地面にできたへいの影の面積は何m²ですか
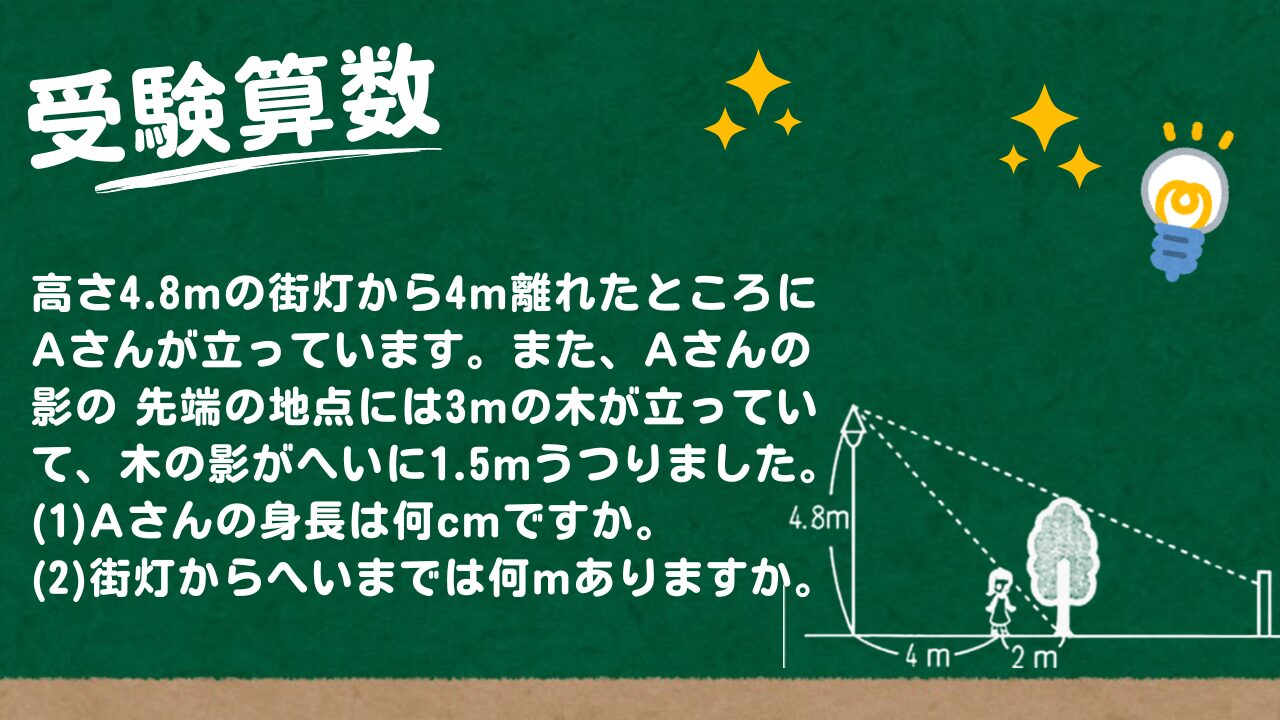
【受験算数】高さ4.8mの街灯から4m離れたところにAさんが立っています。また、Aさんの影の 先端の地点には3mの木が立っていて、木の影がへいに1.5mうつりました。Aさんの身長は何cmですか。
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
高さ4.8mの街灯から4m離れたところにAさんが立っています。また、Aさんの影の 先端の地点には3mの木が立っていて、木の影がへいに1.5mうつりました。次の問 に答えよ。 (1)Aさんの身長は何cmですか。 (2)街灯からへいまでは何mありますか。
この動画を見る
高さ4.8mの街灯から4m離れたところにAさんが立っています。また、Aさんの影の 先端の地点には3mの木が立っていて、木の影がへいに1.5mうつりました。次の問 に答えよ。 (1)Aさんの身長は何cmですか。 (2)街灯からへいまでは何mありますか。
【受験算数】図の三角形ABCは直角三角形、三角形DEFは直角二等辺三角形です。FCの長さは 5cmです。三角形GFCの面積は何cm²ですか。

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図の三角形ABCは直角三角形、三角形DEFは直角二等辺三角形です。
FCの長さは 5cmです。三角形GFCの面積は何cm²ですか。
この動画を見る
右図の三角形ABCは直角三角形、三角形DEFは直角二等辺三角形です。
FCの長さは 5cmです。三角形GFCの面積は何cm²ですか。
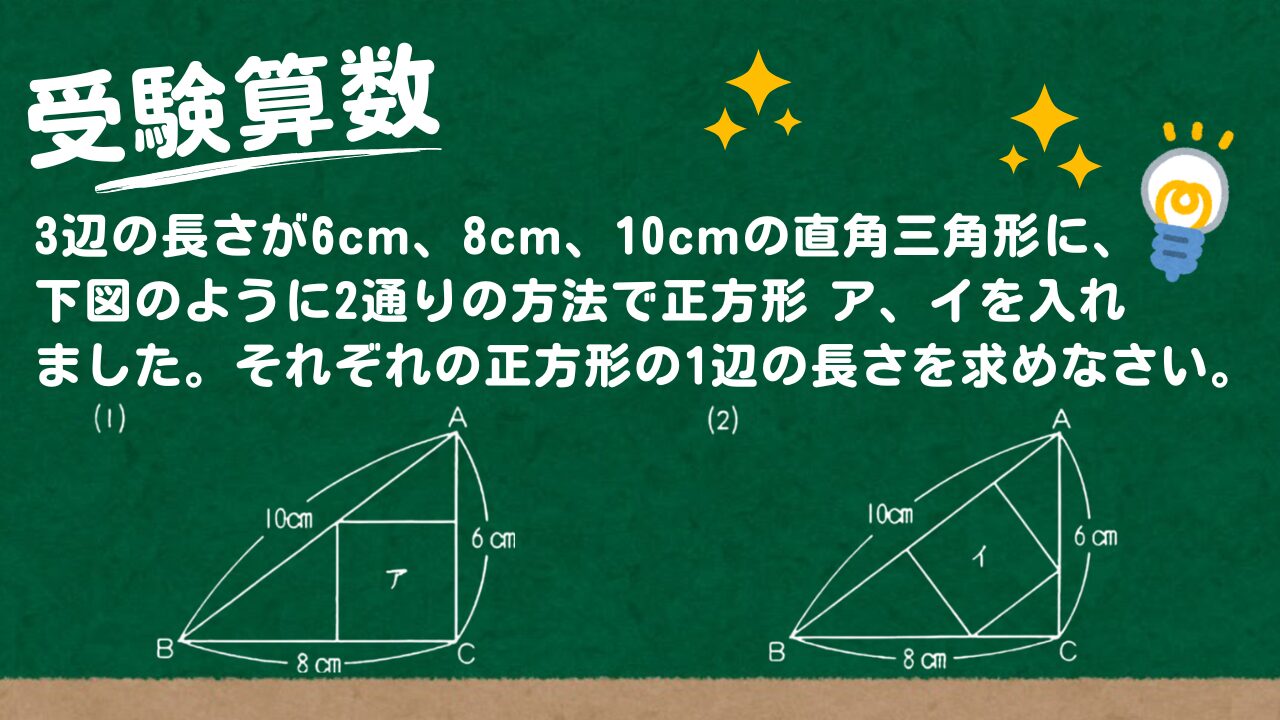
3辺の長さが6cm、8cm、10cmの直角三角形に、下図のように2通りの方法で正方形 ア、イを入れました。それぞれの正方形の1辺の長さを求めなさい。
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さが6cm、8cm、10cmの直角三角形に、下図のように2通りの方法で正方形 ア、イを入れました。それぞれの正方形の1辺の長さを求めなさい。
この動画を見る
3辺の長さが6cm、8cm、10cmの直角三角形に、下図のように2通りの方法で正方形 ア、イを入れました。それぞれの正方形の1辺の長さを求めなさい。
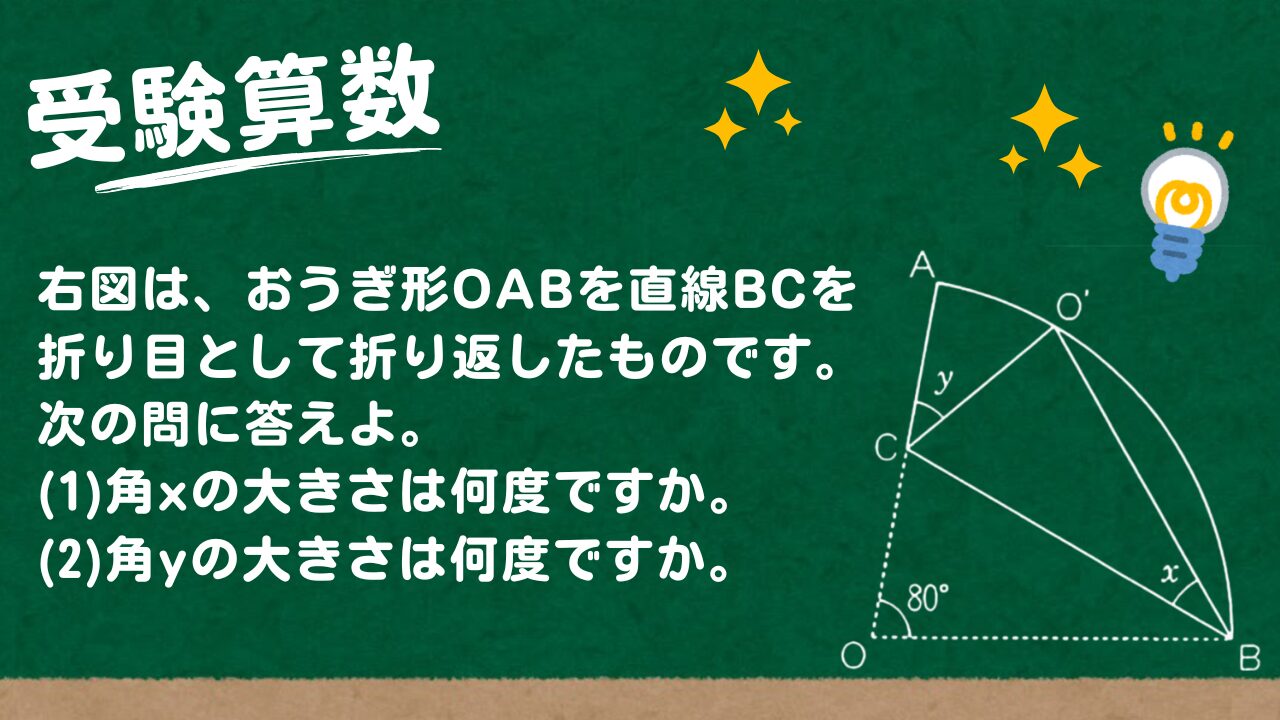
【受験算数】平面図形と比(3):おうぎ形OABを直線BCを折り目として折り返したものです。次の問に答えよ。 (1)角xの大きさは何度ですか。 (2)角yの大きさは何度ですか。
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図は、おうぎ形OABを直線BCを折り目として折り返したものです。次の問に答 えよ。 (1)角xの大きさは何度ですか。 (2)角yの大きさは何度ですか。
この動画を見る
右図は、おうぎ形OABを直線BCを折り目として折り返したものです。次の問に答 えよ。 (1)角xの大きさは何度ですか。 (2)角yの大きさは何度ですか。
【ドラゴン桜】英検2次試験直前にありがたいアドバイスをする桜木先生?

【受験算数】平面図形と比(3):ある時刻に、長さ80cmの棒を地面に垂直に立てたところ、長さ160cmの影が地面にできました。同じ時刻に、地面に垂直に立っている身長1.4mの人の影の長さは何mですか。

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある時刻に、長さ80cmの棒を地面に垂直に立てたところ、長さ160cmの影が地面 にできました。次の問に答えよ。
(1)同じ時刻に、地面に垂直に立っている身長1.4mの人の影の長さは何mですか。
(2)同じ時刻に、高さ5mの木の影がへいの高さ50cmのところまでうつりました。 木とへいの間の距離(図のx)は何mですか。
この動画を見る
ある時刻に、長さ80cmの棒を地面に垂直に立てたところ、長さ160cmの影が地面 にできました。次の問に答えよ。
(1)同じ時刻に、地面に垂直に立っている身長1.4mの人の影の長さは何mですか。
(2)同じ時刻に、高さ5mの木の影がへいの高さ50cmのところまでうつりました。 木とへいの間の距離(図のx)は何mですか。
【受験算数】平面図形と比(3):右図は、長方形ABCDを、AEを折り目として折り返したものです。次の問に答えよ。 (1)DBの長さは何cmですか。 (2)三角形ABEの面積は何cm²ですか。

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
教材:
#予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図は、長方形ABCDを、AEを折り目として折り返したものです。次の問に答えよ。
(1)DBの長さは何cmですか。
(2)三角形ABEの面積は何cm²ですか。
この動画を見る
右図は、長方形ABCDを、AEを折り目として折り返したものです。次の問に答えよ。
(1)DBの長さは何cmですか。
(2)三角形ABEの面積は何cm²ですか。
ダースベイダーと校長先生がEminemを歌いました。

単元:
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師:
理数個別チャンネル
問題文全文(内容文):
ダースベイダーと校長先生がEminemを歌ってみた.
この動画を見る
ダースベイダーと校長先生がEminemを歌ってみた.
【英語】英語なぞなぞガチバトル!英語に慣れ親しもう!

単元:
#英語(高校生)#勉強法・その他#その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
にしもっティー VS Ret's study! VSホーン・フィールド
まどか先生の放った渾身の『英語なぞなぞ』で死闘を繰り広げたその結果は…!?
■問題文全文
Q1 What begins with T, ends with T, and has T in it?
Q2 What goes around the world but stays in a corner?
Q3 Where does today come before yesterday?
Q4 What can you catch but not throw?
Q5 What letter of the alphabet has the most water?
この動画を見る
にしもっティー VS Ret's study! VSホーン・フィールド
まどか先生の放った渾身の『英語なぞなぞ』で死闘を繰り広げたその結果は…!?
■問題文全文
Q1 What begins with T, ends with T, and has T in it?
Q2 What goes around the world but stays in a corner?
Q3 Where does today come before yesterday?
Q4 What can you catch but not throw?
Q5 What letter of the alphabet has the most water?
【英語】高校英文法:関係代名詞の4択問題の解法

単元:
#英語(高校生)#英文法#関係代名詞・関係副詞・複合関係詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題 He is not the man ( ) he was when I first knew him.
①that ②what ③who ④whom 空欄に適する語句はどれ?
この動画を見る
問題 He is not the man ( ) he was when I first knew him.
①that ②what ③who ④whom 空欄に適する語句はどれ?
【数学】2次関数:明大明治2020年度大問5 解説

単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$y=-ⅹ^2$上に点A,Bがあり、点Aのⅹ座標をaとすると直線ℓはー2a+1となった。この時の点Bの座標をa,を用いて表せ。【明大明治 過去問 2020】【二次関数】
この動画を見る
2次関数$y=-ⅹ^2$上に点A,Bがあり、点Aのⅹ座標をaとすると直線ℓはー2a+1となった。この時の点Bの座標をa,を用いて表せ。【明大明治 過去問 2020】【二次関数】
【数学】相似な図形:相似の考え方!
【数学】(高2生必見!!)2019年度 第3回 K塾高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1:小問集合
(1)2次不等式$x^2+5x-6\lt 0$を解け。
(2)9人の生徒を3人ずつA,B,Cの3つの組に分けるとき、分け方は何通りか。
(3)次のデータがある。3,5,5,6,7,10.このデータの平均値を求めよ。また、分散を求めよ。
(4)$(4x+1)^5$を展開したとき、$x^2$の係数を求めよ。
(5)xの整式$x^3-3x^2+ax-a$ (aは定数)がx-2で割り切れるとき、aの値を求めよ。
(6)$a\neq 0,b\neq 0$とする。 $(ab)^5\times (a^2)^{-3}\div (b^2)^2$を計算せよ。
(7)整数m,nについて、$m+n$が偶数であることは、mnが偶数であるための$\Box$である。
(選択肢)
①必要十分条件である
②必要条件であるが、十分条件ではない
③十分条件であるが、必要条件ではない
④必要条件でも十分条件でもない
大問2[1]:式と証明
次のような問題がある。
問1 すべての実数xに対して、不等式 $x^2+x+1\geqq 3x-2 …$(*)が成り立つことを証明せよ。
問2 $x\geqq 2$のとき、関数$ f(x)=\dfrac{x+2}{x}$ の最小値を求めよ。
太郎さんはこの問題の解答を次のように書いた。
問1 $(x^2+x+1)-(3x-2)=x^2-2x+3=(a-1)^2+2$ すべての実数xに対して、$(x-1)^2\geqq 0$であるから、$(a-1)^2+2\geqq 0$ よって、$x^2+x+1\geqq 3x-2$ は成り立つ。
問2 $x\geqq 2$のとき、$x\gt 0,\dfrac{2}{x}\gt 0$であるから、相加平均と相乗平均の大小関係より、$\dfrac{x+2}{x}\geqq 2\sqrt x\times \dfrac{2}{x}$ これより、$f(x)\geqq 2\sqrt2$ よって、f(x)の最小値は$2\sqrt2$である。
(1)太郎さんの問1の解答は正しいか、正しくないか答えよ(答えのみでよい)。また、xが実数のとき、問1の不等式(*)において、等号が成り立つか成り立たないか答えよ。さらに、その理由を「実数」「実数解」のいずれかの単語を用いて説明せよ。
大問2[2]:確率
1~4の数字が書かれたカードが1枚ずつ計4枚のカードが入っている袋がある。この袋の中から1枚のカードを無作為に取り出し、カードに書かれた数を記録して袋に戻すことを繰り返し4回行う。
(1)4回とも1が記録される確率を求めよ。
(2)4回とも2以上の数が記録される確率を求めよ。
(3)記録された4個の数の最小値が2である確率を求めよ。
大問3:図形と方程式
aは実数の定数とする。xy平面上に2点A(1,0)、B(-1,4)と円C:$x^2+y^2-2(a+1)x-4ay+5a^2+2a=0$があり、Cの中心をPとする。
(1)線分ABの長さと、直線ABの方程式を求めよ。
(2)$a=1$のとき、Pの座標を求めよ。また、このときのPと直線ABの距離を求めよ。
(3)aが実数全体を変化するとき、Pの軌跡を求めよ。
(4)aの値が$1\leqq a\leqq 3$の範囲を変化するとき、Cが通過する領域をDとする。点QがDを動くとき、三角形ABQの面積の最小値と最大値をそれぞれ求めよ。
大問4:三角関数
座標平面上に2点A(8,0)、B(0,8)と、原点を中心とする半径3の円がある。この円上に、x座標、y座標がともに正である点P($3\cos\theta,3\sin\theta)\left(0\lt\theta\lt \dfrac{\pi}{2}\right)$をとる。Pからx軸に下した垂線とx軸の交点をQ、Pからy軸に下した垂線とy軸の交点をRとし、△APQと△BPRの面積の和をSとする。
(1)線分AB、BRの長さをそれぞれ$\sin\theta、\cos\theta$を用いて表せ。
(2)Sを$\sin\theta、\cos\theta$を用いて表せ。
(3)$t=\sin\theta+\cos\theta$とする。$\theta$が$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、tのとり得る値の範囲を求めよ。
(4)(i)θが$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、Sの最大値を求めよ。
(ii)Sが最大となる$\theta$は2つあり、それらを$\theta_1,\theta_2\left(0\lt\theta_1\lt\theta_2\lt\dfrac{\pi}{2}\right)$とする。このとき、$\dfrac{\pi}{8}\lt \theta_1\lt\dfrac{\pi}{6}$であることを証明せよ。
大問5:微分法
3次関数 $f(x)=2x^3+3(1-a)x^2-6ax+8a$ がある。ただし、aは実数の定数である。
(1)a=2とする。
(i)f(x)の増減を調べて、f(x)の極大値と極小値を求めよ。
(ii)xの方程式$f(x)=0$の解で、$1\lt x\lt2$を満たすものの個数を求めよ。
(2)f(x)が$1\lt x\lt 2$において極値をもたないようなaの値の範囲を求めよ。
(3)xの方程式$f(x)=0$が$1\lt x\lt 2$の範囲に少なくとも1つの解をもつようなaの値の範囲を求めよ。
大問6:ベクトル
Oを原点とする座標空間に、3点A(1,2,2)、B(3,-4,0)、C(a,b,5)があり、$OA⊥OC$かつ$OB⊥OC$が成り立っている。
(1)$\vert OA\vert$、$\vert OB\vert$、内積$OA・OB、\cos\angle AOB$の値をそれぞれ求めよ。
(2)a,bの値を求めよ。
(3)四面体OABCの体積を求めよ。
(4)Oを中心とする半径rの球面Sがある。Sが3点A,B,Cを通る平面と交わってできる円の半径が2であるとき、rの値を求めよ。
大問7:数列
数列{$a_n$}$(n=1,2,3,…)$を$a_1=7, a_{n+1}=a_n+4(n=1,2,3,…)$によって定める。
(1)$a_4$の値を求めよ。また、数列{$a_n$}の一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^n a_k$を求めよ。
(3)数列{$b_n$}$(n=1,2,3,…)$を$b_1=3, b_{n+1}-b_n=a_n(n=1,2,3,…)$によって定める。数列{$b_n$}の一般項$b_n$を求めよ。
(4)数列{$c_n$}$(n=1,2,3,…)$を(3)の$b_n$を用いて、$c_1=\dfrac{1}{5}, c_{n+1}=b_n\times \dfrac{c_n}{(b_{n+1}-3)}(n=1,2,3,…)$によって定める。数列${c_n}$の一般項$c_n$を求めよ。また、$\displaystyle \sum_{k=1}^n c_k$を求めよ。
この動画を見る
大問1:小問集合
(1)2次不等式$x^2+5x-6\lt 0$を解け。
(2)9人の生徒を3人ずつA,B,Cの3つの組に分けるとき、分け方は何通りか。
(3)次のデータがある。3,5,5,6,7,10.このデータの平均値を求めよ。また、分散を求めよ。
(4)$(4x+1)^5$を展開したとき、$x^2$の係数を求めよ。
(5)xの整式$x^3-3x^2+ax-a$ (aは定数)がx-2で割り切れるとき、aの値を求めよ。
(6)$a\neq 0,b\neq 0$とする。 $(ab)^5\times (a^2)^{-3}\div (b^2)^2$を計算せよ。
(7)整数m,nについて、$m+n$が偶数であることは、mnが偶数であるための$\Box$である。
(選択肢)
①必要十分条件である
②必要条件であるが、十分条件ではない
③十分条件であるが、必要条件ではない
④必要条件でも十分条件でもない
大問2[1]:式と証明
次のような問題がある。
問1 すべての実数xに対して、不等式 $x^2+x+1\geqq 3x-2 …$(*)が成り立つことを証明せよ。
問2 $x\geqq 2$のとき、関数$ f(x)=\dfrac{x+2}{x}$ の最小値を求めよ。
太郎さんはこの問題の解答を次のように書いた。
問1 $(x^2+x+1)-(3x-2)=x^2-2x+3=(a-1)^2+2$ すべての実数xに対して、$(x-1)^2\geqq 0$であるから、$(a-1)^2+2\geqq 0$ よって、$x^2+x+1\geqq 3x-2$ は成り立つ。
問2 $x\geqq 2$のとき、$x\gt 0,\dfrac{2}{x}\gt 0$であるから、相加平均と相乗平均の大小関係より、$\dfrac{x+2}{x}\geqq 2\sqrt x\times \dfrac{2}{x}$ これより、$f(x)\geqq 2\sqrt2$ よって、f(x)の最小値は$2\sqrt2$である。
(1)太郎さんの問1の解答は正しいか、正しくないか答えよ(答えのみでよい)。また、xが実数のとき、問1の不等式(*)において、等号が成り立つか成り立たないか答えよ。さらに、その理由を「実数」「実数解」のいずれかの単語を用いて説明せよ。
大問2[2]:確率
1~4の数字が書かれたカードが1枚ずつ計4枚のカードが入っている袋がある。この袋の中から1枚のカードを無作為に取り出し、カードに書かれた数を記録して袋に戻すことを繰り返し4回行う。
(1)4回とも1が記録される確率を求めよ。
(2)4回とも2以上の数が記録される確率を求めよ。
(3)記録された4個の数の最小値が2である確率を求めよ。
大問3:図形と方程式
aは実数の定数とする。xy平面上に2点A(1,0)、B(-1,4)と円C:$x^2+y^2-2(a+1)x-4ay+5a^2+2a=0$があり、Cの中心をPとする。
(1)線分ABの長さと、直線ABの方程式を求めよ。
(2)$a=1$のとき、Pの座標を求めよ。また、このときのPと直線ABの距離を求めよ。
(3)aが実数全体を変化するとき、Pの軌跡を求めよ。
(4)aの値が$1\leqq a\leqq 3$の範囲を変化するとき、Cが通過する領域をDとする。点QがDを動くとき、三角形ABQの面積の最小値と最大値をそれぞれ求めよ。
大問4:三角関数
座標平面上に2点A(8,0)、B(0,8)と、原点を中心とする半径3の円がある。この円上に、x座標、y座標がともに正である点P($3\cos\theta,3\sin\theta)\left(0\lt\theta\lt \dfrac{\pi}{2}\right)$をとる。Pからx軸に下した垂線とx軸の交点をQ、Pからy軸に下した垂線とy軸の交点をRとし、△APQと△BPRの面積の和をSとする。
(1)線分AB、BRの長さをそれぞれ$\sin\theta、\cos\theta$を用いて表せ。
(2)Sを$\sin\theta、\cos\theta$を用いて表せ。
(3)$t=\sin\theta+\cos\theta$とする。$\theta$が$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、tのとり得る値の範囲を求めよ。
(4)(i)θが$0\lt\theta\lt\dfrac{\pi}{2}$の範囲を変化するとき、Sの最大値を求めよ。
(ii)Sが最大となる$\theta$は2つあり、それらを$\theta_1,\theta_2\left(0\lt\theta_1\lt\theta_2\lt\dfrac{\pi}{2}\right)$とする。このとき、$\dfrac{\pi}{8}\lt \theta_1\lt\dfrac{\pi}{6}$であることを証明せよ。
大問5:微分法
3次関数 $f(x)=2x^3+3(1-a)x^2-6ax+8a$ がある。ただし、aは実数の定数である。
(1)a=2とする。
(i)f(x)の増減を調べて、f(x)の極大値と極小値を求めよ。
(ii)xの方程式$f(x)=0$の解で、$1\lt x\lt2$を満たすものの個数を求めよ。
(2)f(x)が$1\lt x\lt 2$において極値をもたないようなaの値の範囲を求めよ。
(3)xの方程式$f(x)=0$が$1\lt x\lt 2$の範囲に少なくとも1つの解をもつようなaの値の範囲を求めよ。
大問6:ベクトル
Oを原点とする座標空間に、3点A(1,2,2)、B(3,-4,0)、C(a,b,5)があり、$OA⊥OC$かつ$OB⊥OC$が成り立っている。
(1)$\vert OA\vert$、$\vert OB\vert$、内積$OA・OB、\cos\angle AOB$の値をそれぞれ求めよ。
(2)a,bの値を求めよ。
(3)四面体OABCの体積を求めよ。
(4)Oを中心とする半径rの球面Sがある。Sが3点A,B,Cを通る平面と交わってできる円の半径が2であるとき、rの値を求めよ。
大問7:数列
数列{$a_n$}$(n=1,2,3,…)$を$a_1=7, a_{n+1}=a_n+4(n=1,2,3,…)$によって定める。
(1)$a_4$の値を求めよ。また、数列{$a_n$}の一般項$a_n$を求めよ。
(2)$\displaystyle \sum_{k=1}^n a_k$を求めよ。
(3)数列{$b_n$}$(n=1,2,3,…)$を$b_1=3, b_{n+1}-b_n=a_n(n=1,2,3,…)$によって定める。数列{$b_n$}の一般項$b_n$を求めよ。
(4)数列{$c_n$}$(n=1,2,3,…)$を(3)の$b_n$を用いて、$c_1=\dfrac{1}{5}, c_{n+1}=b_n\times \dfrac{c_n}{(b_{n+1}-3)}(n=1,2,3,…)$によって定める。数列${c_n}$の一般項$c_n$を求めよ。また、$\displaystyle \sum_{k=1}^n c_k$を求めよ。
【英語語彙】英単語 bearの「複数の意味」の覚え方

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
bearには色々な意味がありますが、どうやって覚えるかを明快に解説します! #多義語
この動画を見る
bearには色々な意味がありますが、どうやって覚えるかを明快に解説します! #多義語
【日本史】仏教伝来の流れを確認しよう

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#日本史#歴史#歴史#原始・古代
指導講師:
理数個別チャンネル
問題文全文(内容文):
日本にいつ、どのように仏教が伝わったのか、「日本史」の入試の観点で解説します。
この動画を見る
日本にいつ、どのように仏教が伝わったのか、「日本史」の入試の観点で解説します。
【英語】文法問題で出る!as for Aとas to Aの違い【群前置詞】

単元:
#英語(高校生)#英文法#前置詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
as for, as to, as with, as in, as ofなどの群前置詞の意味の違いや用法は知っていますか?
この動画を見る
as for, as to, as with, as in, as ofなどの群前置詞の意味の違いや用法は知っていますか?
【数Ⅱ】三角関数:方程式6x²-xy-y²=0は交わる2直線を表す。このとき、2直線のなす角θ(0≦θ≦π/2)を求めよ。

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$6x^2-xy-y^2=0$は交わる2直線を表す。このとき、2直線のなす角$\theta(0\leqq\theta\leqq \dfrac{\pi}{2}$)を求めよ。
この動画を見る
方程式$6x^2-xy-y^2=0$は交わる2直線を表す。このとき、2直線のなす角$\theta(0\leqq\theta\leqq \dfrac{\pi}{2}$)を求めよ。
【数Ⅱ】三角関数:方程式sin(θ+40°)=sinθ(ただし0°≦θ≦90°)をみたすθを求めよ。

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$\sin(\theta+40°)=\sin\theta$(ただし$0°\leqq\theta\leqq90°$)をみたす$\theta$を求めよ。
この動画を見る
方程式$\sin(\theta+40°)=\sin\theta$(ただし$0°\leqq\theta\leqq90°$)をみたす$\theta$を求めよ。
【受験理科】地層と岩石④:『地層のでき方と読み取り方』
単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
地層と岩石④:『地層のでき方と読み取り方』
「地層はどうやって生まれる?」
「地層からの情報の読み取り方」
この動画を見る
地層と岩石④:『地層のでき方と読み取り方』
「地層はどうやって生まれる?」
「地層からの情報の読み取り方」
【受験理科】地層と岩石③:『レキ岩・砂岩・泥岩の積もり方』

単元:
#理科(中学受験)#地学分野
指導講師:
理数個別チャンネル
問題文全文(内容文):
地層と岩石③:『レキ岩・砂岩・泥岩の積もり方』
「堆積岩はどのように生まれるか?」
「レキ岩・砂岩・泥岩の積もり方」
この動画を見る
地層と岩石③:『レキ岩・砂岩・泥岩の積もり方』
「堆積岩はどのように生まれるか?」
「レキ岩・砂岩・泥岩の積もり方」




