 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【英語】助動詞:used toにアメリカの空港で出会った!

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#助動詞#会話文
指導講師:
理数個別チャンネル
問題文全文(内容文):
used toという助動詞は、入試でもよく見かけますが実生活ではどのように使われていたかチェック!
この動画を見る
used toという助動詞は、入試でもよく見かけますが実生活ではどのように使われていたかチェック!
【理数個別の過去問解説】1976年度東京工業大学 数学 第1問解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
p(x)をxに関する3次式とする。$x^4$と$x^5$をp(x)で割った余りは等しくて、0ではないとする。
xの整式f(x)がp(x)で割り切れず、xf(x)はp(x)で割り切れるとき、 f(x)をp(x)で割った余りr(x)を求めよ。
ただし、r(x)の最高次係数は1となるものとする。
この動画を見る
p(x)をxに関する3次式とする。$x^4$と$x^5$をp(x)で割った余りは等しくて、0ではないとする。
xの整式f(x)がp(x)で割り切れず、xf(x)はp(x)で割り切れるとき、 f(x)をp(x)で割った余りr(x)を求めよ。
ただし、r(x)の最高次係数は1となるものとする。
【数A】整数の性質:慶應義塾大学 1の位の数は?

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
一の位の数(合同式の利用):十進法の表記法で考えよう。
(1)$2^{100}$の一の位の数 字を求めよう。
(2)$3^{1000}$の一の位の数字を求めよう。
(3)$a=3^{33}$とするとき、$3^a$ の一の位の数字を求めよう。
この動画を見る
一の位の数(合同式の利用):十進法の表記法で考えよう。
(1)$2^{100}$の一の位の数 字を求めよう。
(2)$3^{1000}$の一の位の数字を求めよう。
(3)$a=3^{33}$とするとき、$3^a$ の一の位の数字を求めよう。
【超速習】英検面接の極意 ~切り抜き~

【英検】2次試験(スピーキング)で満点を取るためにやるべきこと【準2級+3級・2級】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準2級#英検3級#英語リスニング・スピーキング#勉強法#スピーキング#英検
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検の2次試験で満点を取るためにやるべきことを解説しています
この動画を見る
英検の2次試験で満点を取るためにやるべきことを解説しています
【英検準2級】2次試験(スピーキング)で満点を取るためにやるべきこと

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級#英語リスニング・スピーキング#スピーキング#スピーキングその他
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次試験(スピーキング)で満点を取るためにやるべきことに関して解説していきます.
この動画を見る
2次試験(スピーキング)で満点を取るためにやるべきことに関して解説していきます.
【受験理科】熱量(カロリー):温度の違う2つの水を混ぜると何℃?

単元:
#物理#熱・波・音#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)10℃の水100gと60℃の水100gを混ぜると何℃になるか求めよ。
(2)20℃の水100gと□gの水400gを混ぜると28℃になった。□を求めよ。
この動画を見る
(1)10℃の水100gと60℃の水100gを混ぜると何℃になるか求めよ。
(2)20℃の水100gと□gの水400gを混ぜると28℃になった。□を求めよ。
【受験算数】AとBの速さの比を3:2とする。ある池のまわりを2人が同じ場所から同時に反対方向に向かって歩くと2人は1周目の途中で初めて出会い、Aは出発地点から72m通り過ぎたところでBと再び出会った…

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
理数個別チャンネル
問題文全文(内容文):
AとBの速さの比を3:2とする。ある池のまわりを、2人が同じ場所から同時に反対方向に向かって歩くと2人は1周目の途中で初めて出会い、Aは出発地点から72m通り過ぎたところでBと再び出会った。この池のまわりの長さは何m?
この動画を見る
AとBの速さの比を3:2とする。ある池のまわりを、2人が同じ場所から同時に反対方向に向かって歩くと2人は1周目の途中で初めて出会い、Aは出発地点から72m通り過ぎたところでBと再び出会った。この池のまわりの長さは何m?
【理数個別の過去問解説】2015年度京都大学 数学 文系第3問解説

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
6個の点A,B,C,D,E,Fが右図のように長さ1の線分で結ばれているとする。
各線分 をそれぞれ独立に確率1/2で赤または黒で塗る。
赤く塗られた線分だけを通って 点Aから点Eにいたる経路がある場合はそのうちで最短のものの長さをXとする。 そのような経路がない場合はX=0とする。
このとき、n=0,2,4について、X=nとな る確率を求めよう。
この動画を見る
6個の点A,B,C,D,E,Fが右図のように長さ1の線分で結ばれているとする。
各線分 をそれぞれ独立に確率1/2で赤または黒で塗る。
赤く塗られた線分だけを通って 点Aから点Eにいたる経路がある場合はそのうちで最短のものの長さをXとする。 そのような経路がない場合はX=0とする。
このとき、n=0,2,4について、X=nとな る確率を求めよう。
【理数個別の過去問解説】2007年度京都大学 数学 理系第1問(2)解説

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
得点1,2,...,nが等しい確率で得られるゲームを独立に3回繰り返す。
このとき、 2回目の得点が1回目の得点以上であり、さらに3回目の特典が2回目の得点以上となる確率を求めよう。
この動画を見る
得点1,2,...,nが等しい確率で得られるゲームを独立に3回繰り返す。
このとき、 2回目の得点が1回目の得点以上であり、さらに3回目の特典が2回目の得点以上となる確率を求めよう。
【英検2級】1次試験の予想配点と合格ライン

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
1次試験の予想配点と合格ラインに関して解説していきます.
この動画を見る
1次試験の予想配点と合格ラインに関して解説していきます.
【英検準2級】1次試験の予想配点と合格ライン

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
1次試験の予想配点と合格ラインに関して解説していきます.
この動画を見る
1次試験の予想配点と合格ラインに関して解説していきます.
【数Ⅰ】数と式:分母にxを含む不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解きなさい。
$\dfrac{1}{x-2} ≦ \dfrac{2}{x+3}$
この動画を見る
次の不等式を解きなさい。
$\dfrac{1}{x-2} ≦ \dfrac{2}{x+3}$
【数A】確率:確率の最大

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
さいころを1000回投げるとき、1の目がちょうどk回出る確率を$P_k$とする。
$P_k$が最大となるkを求めよ。
この動画を見る
さいころを1000回投げるとき、1の目がちょうどk回出る確率を$P_k$とする。
$P_k$が最大となるkを求めよ。
【理数個別の過去問解説】2021年度東京大学 数学 理科・文科第4問(4)解説

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
東京大学 2021年理科・文科第4問(4)
以下の問いに答えよ。
(1)正の奇数K,Lと正の整数A,BがKA=LBを満たしているとする。Kを4で割った余りがLを4で割った余りと等しいならば、Aを4で割った余りはBを4で割った余りと等しいことを示せ。
(2)正の整数a,bがa>bを満たしているとする。このとき、$A=_{4a+1}C_{4b+1},B={}_a\mathrm{C}_b$に対してKA=LBとなるような正の奇数K,Lが存在することを示せ。
(3)a,bは(2)の通りとし、さらにa-bが2で割り切れるとする。${}_{4a+1}\mathrm{C}_{4b+1}wp4$で割った余りは${}_a\mathrm{C}_b$を4で割った余りと等しいことを示せ。
(4)2021C37を4で割った余りを求めよ。
この動画を見る
東京大学 2021年理科・文科第4問(4)
以下の問いに答えよ。
(1)正の奇数K,Lと正の整数A,BがKA=LBを満たしているとする。Kを4で割った余りがLを4で割った余りと等しいならば、Aを4で割った余りはBを4で割った余りと等しいことを示せ。
(2)正の整数a,bがa>bを満たしているとする。このとき、$A=_{4a+1}C_{4b+1},B={}_a\mathrm{C}_b$に対してKA=LBとなるような正の奇数K,Lが存在することを示せ。
(3)a,bは(2)の通りとし、さらにa-bが2で割り切れるとする。${}_{4a+1}\mathrm{C}_{4b+1}wp4$で割った余りは${}_a\mathrm{C}_b$を4で割った余りと等しいことを示せ。
(4)2021C37を4で割った余りを求めよ。
【数Ⅰ】図形と計量:三角比の表④演習 (1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。
この動画を見る
(1)sin60°(2)cos45°(3)tan120°(4)cos90°の値を求めよ。
【数Ⅰ】図形と計量:三角比の表③

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・sin0°, sin90°, sin180°の値を求めよ。
・cos0°, cos90°, cos180°の値を求めよ。
・tan0°, tan90°, tan180°の値を求めよ。
この動画を見る
・sin0°, sin90°, sin180°の値を求めよ。
・cos0°, cos90°, cos180°の値を求めよ。
・tan0°, tan90°, tan180°の値を求めよ。
【英検準1級】④ライティング:ボディ(理由部分)を「メモ作成」から「本書き」まで見せます!

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準1級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
<Agree/Disagree>
More needs to be done to improve public safety.
●Accidents
●Crime
●Food
●Technology
この動画を見る
<Agree/Disagree>
More needs to be done to improve public safety.
●Accidents
●Crime
●Food
●Technology
【英検2級】ライティング:コメント欄の質問に答えてみました。(thatがない問題の場合はどうすればいいの?)

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people prefer to buy food produced in their local area. Do you think more people will buy locally produced food in the future?
●Local economies
●Safety
●The environment
この動画を見る
Some people prefer to buy food produced in their local area. Do you think more people will buy locally produced food in the future?
●Local economies
●Safety
●The environment
【英検準1級】③ライティング:動画①②で教えた「思考の手順」と「魔法のテンプレ」を使って実際の問題を10分で解いてみた。

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準1級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
<Agree/Disagree>
More needs to be done to improve public safety.
●Accidents
●Crime
●Food
●Technology
この動画を見る
<Agree/Disagree>
More needs to be done to improve public safety.
●Accidents
●Crime
●Food
●Technology
【受験算数】空間図形:一辺が10㎝の直方体ABCD-EFGHがある。この直方体をAPQRで切断した。DP=4㎝、HQ=8㎝の時、ERの長さは何㎝か求めよ。
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#予習シ#予習シ算数・小5下#中学受験教材#立方体・直方体の切断
指導講師:
理数個別チャンネル
問題文全文(内容文):
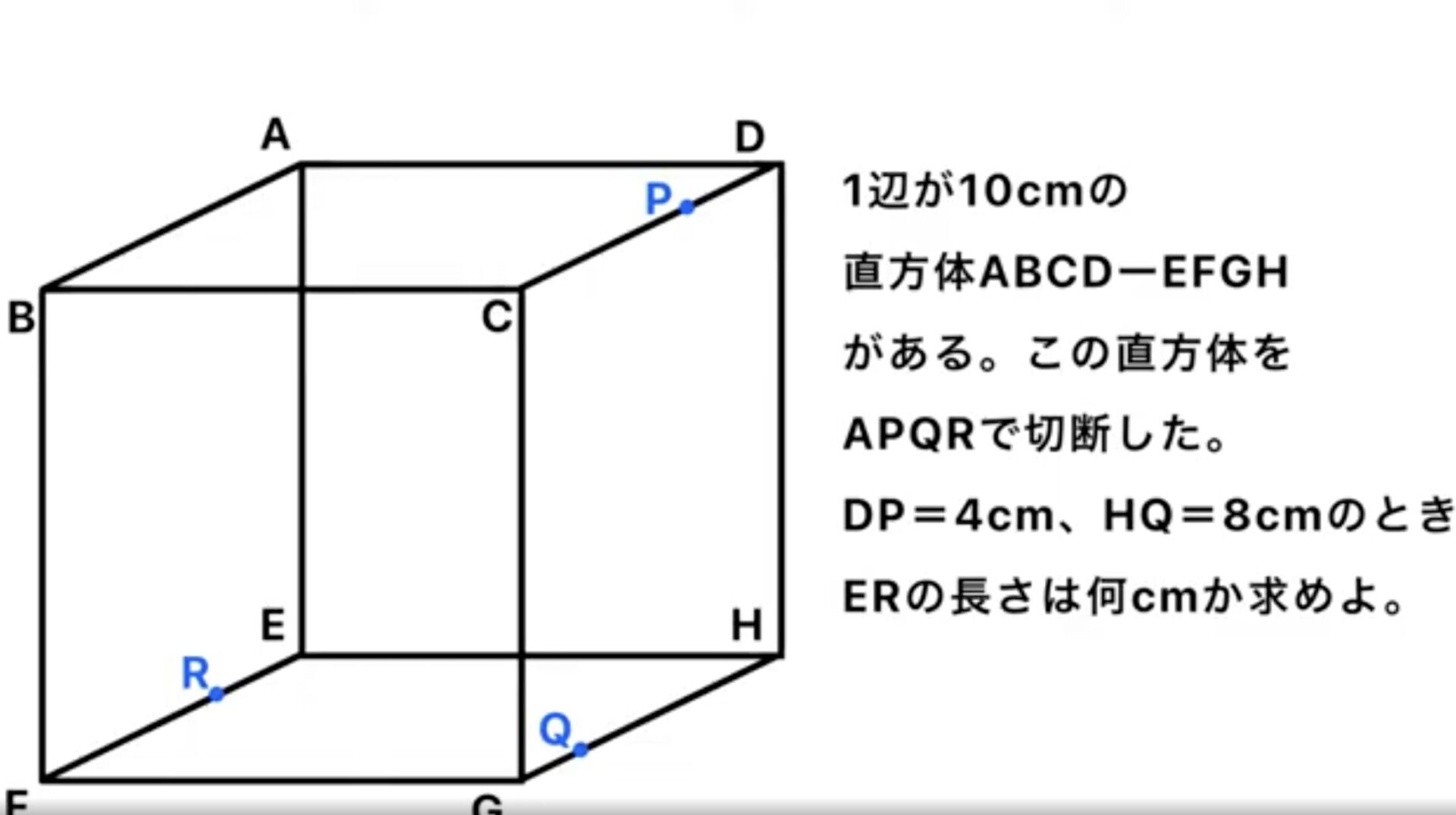
一辺が10㎝の直方体ABCD-EFGHがある。この直方体をAPQRで切断した。DP=4㎝、HQ=8㎝の時、ERの長さは何㎝か求めよ。【空間図形】
この動画を見る
一辺が10㎝の直方体ABCD-EFGHがある。この直方体をAPQRで切断した。DP=4㎝、HQ=8㎝の時、ERの長さは何㎝か求めよ。【空間図形】
【受験算数】空間図形:下の図は、同じ大きさの立方体の積み木を積み重ねてできた立体を、正面、右側、真上から見た図を表しています。積み重ねてある積み木は何個でしょう。
単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#予習シ#予習シ算数・小5下#中学受験教材#立方体・直方体の切断
指導講師:
理数個別チャンネル
問題文全文(内容文):
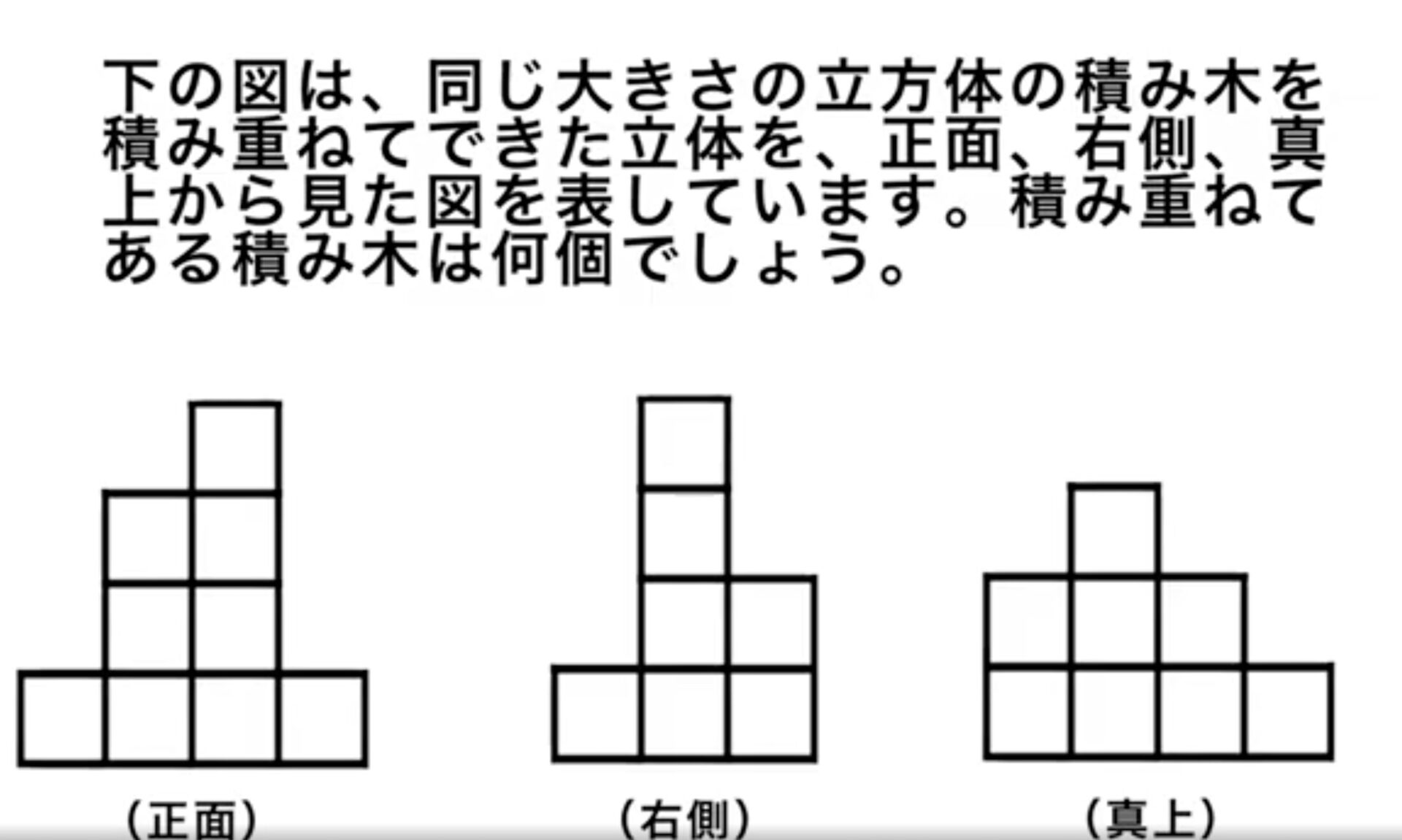
下の図は、同じ大きさの立方体の積み木を積み重ねてできた立体を、正面、右側、真上から見た図を表しています。積み重ねてある積み木はなんかでしょう。【予習シリーズ 6年生】【空間図形】
この動画を見る
下の図は、同じ大きさの立方体の積み木を積み重ねてできた立体を、正面、右側、真上から見た図を表しています。積み重ねてある積み木はなんかでしょう。【予習シリーズ 6年生】【空間図形】
英検準1級ライティングを短時間で8割得点保証のチート技公開(150語のうち自分で考えるのは80語だけ)※固定コメ欄に訂正あり

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準1級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
<Agree/Disagree>
More people should become vegetarians in the future.
●Animal rights
●Cost
●Environment
●Health
この動画を見る
<Agree/Disagree>
More people should become vegetarians in the future.
●Animal rights
●Cost
●Environment
●Health
【数A】整数の性質:最大公約数と最小公倍数の性質

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学A 整数の性質】
(1)自然数nと30の最大公約数が6、最小公倍数が120であるとき、このnを求めよ。
(2)和が280、最大公約数が14となる自然数aとb(ただしa<bとする)をすべて求めよ。
(出典元)4STEP数学Aより
この動画を見る
【高校数学 数学A 整数の性質】
(1)自然数nと30の最大公約数が6、最小公倍数が120であるとき、このnを求めよ。
(2)和が280、最大公約数が14となる自然数aとb(ただしa<bとする)をすべて求めよ。
(出典元)4STEP数学Aより
【数A】整数の性質:整数の正の約数の個数とその総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学A 場合の数と確率】
12の正の約数の個数とその総和を求めよ。
(出典元)4STEP数学Aより
この動画を見る
【高校数学 数学A 場合の数と確率】
12の正の約数の個数とその総和を求めよ。
(出典元)4STEP数学Aより
【数A】整数の性質:関西学院大学 背理法の利用

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
pを整数とする。
方程式$x^2+4x-5p+2=0$を満足する整数xは存在しないことを証明せよ。
この動画を見る
pを整数とする。
方程式$x^2+4x-5p+2=0$を満足する整数xは存在しないことを証明せよ。
【数A】場合の数:岐阜大学2008年

単元:
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
7個の文字FGGIIUUを横1列に並べる。次の問いに答えよ。
(1)『GIFU』という連続 した4文字が現れるように並べる方法は何通りあるか。
(2)『GI』と『FU』という 連続した2文字がともに現れ、少なくとも1つの『GI』が『FU』よりも左にあるよ うに並べる方法は何通りあるか。
この動画を見る
7個の文字FGGIIUUを横1列に並べる。次の問いに答えよ。
(1)『GIFU』という連続 した4文字が現れるように並べる方法は何通りあるか。
(2)『GI』と『FU』という 連続した2文字がともに現れ、少なくとも1つの『GI』が『FU』よりも左にあるよ うに並べる方法は何通りあるか。
【化学】構造決定:慶應義塾大学薬学部2018年 問4 part 2

単元:
#化学#有機#大学入試過去問(化学)#有機化合物の特徴と構造#脂肪族炭化水素#酸素を含む脂肪族化合物#理科(高校生)#慶應義塾大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
化合物A、B、CおよびDは水素、炭素、酸素、窒素原子のみからなる分子量300以下の化合物であり、すべて8員環の構造を持つ。
化合物A、Bは窒素原子を1つ含み、互いに異性体の関係にある。また、化合物C、Dは窒素原子2つを含み、互いに異性体の関係にある。
79.5 mgの化合物Aを完全燃焼させたところ、二酸化炭素205mgと水27.0mgを生じた。同様に59.5mgの化合物Cからは二酸化炭素154mgと水22.5mgを生じた。
化合物A~Dの溶液に水酸化ナトリウム水溶液を加えて加水分解を進めると、化合物E、F、G、HおよびIのような有機化合物もしくはナトリウム塩が得られた。なお、それぞれの反応生成物はAからはEとF、BからはGとH、CからはHとI、DからはEのみとなっていた。
Aを加水分解して得られた反応液に希塩酸を加えて酸性にし、ジエチルエーテルで抽出を行うと、エーテル層から化合物Fを得ることができた。
同様の操作をBの反応液に行うと、エーテル層から化合物Hを得ることができた。
化合物Eに塩酸と亜硝酸ナトリウムを加え反応させ、その後加温すると化合物Fが生成した。また、化合物Hを加熱すると脱水反応が進行した。
A~Dの構造式をかけ
この動画を見る
化合物A、B、CおよびDは水素、炭素、酸素、窒素原子のみからなる分子量300以下の化合物であり、すべて8員環の構造を持つ。
化合物A、Bは窒素原子を1つ含み、互いに異性体の関係にある。また、化合物C、Dは窒素原子2つを含み、互いに異性体の関係にある。
79.5 mgの化合物Aを完全燃焼させたところ、二酸化炭素205mgと水27.0mgを生じた。同様に59.5mgの化合物Cからは二酸化炭素154mgと水22.5mgを生じた。
化合物A~Dの溶液に水酸化ナトリウム水溶液を加えて加水分解を進めると、化合物E、F、G、HおよびIのような有機化合物もしくはナトリウム塩が得られた。なお、それぞれの反応生成物はAからはEとF、BからはGとH、CからはHとI、DからはEのみとなっていた。
Aを加水分解して得られた反応液に希塩酸を加えて酸性にし、ジエチルエーテルで抽出を行うと、エーテル層から化合物Fを得ることができた。
同様の操作をBの反応液に行うと、エーテル層から化合物Hを得ることができた。
化合物Eに塩酸と亜硝酸ナトリウムを加え反応させ、その後加温すると化合物Fが生成した。また、化合物Hを加熱すると脱水反応が進行した。
A~Dの構造式をかけ
【化学】構造決定:慶應義塾大学薬学部2018年 問4 part 1

単元:
#化学#有機#大学入試過去問(化学)#有機化合物の特徴と構造#理科(高校生)#慶應義塾大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
化合物A、B、CおよびDは水素、炭素、酸素、窒素原子のみからなる分子量300以下の化合物であり、すべて8員環の構造を持つ。
化合物A、Bは窒素原子を1つ含み、互いに異性体の関係にある。また、化合物C、Dは窒素原子2つを含み、互いに異性体の関係にある。
79.5 mgの化合物Aを完全燃焼させたところ、二酸化炭素205mgと水27.0mgを生じた。同様に59.5mgの化合物Cからは二酸化炭素154mgと水22.5mgを生じた。
化合物A~Dの溶液に水酸化ナトリウム水溶液を加えて加水分解を進めると、化合物E、F、G、HおよびIのような有機化合物もしくはナトリウム塩が得られた。なお、それぞれの反応生成物はAからはEとF、BからはGとH、CからはHとI、DからはEのみとなっていた。
Aを加水分解して得られた反応液に希塩酸を加えて酸性にし、ジエチルエーテルで抽出を行うと、エーテル層から化合物Fを得ることができた。
同様の操作をBの反応液に行うと、エーテル層から化合物Hを得ることができた。
化合物Eに塩酸と亜硝酸ナトリウムを加え反応させ、その後加温すると化合物Fが生成した。また、化合物Hを加熱すると脱水反応が進行した。
A~Dの構造式をかけ
この動画を見る
化合物A、B、CおよびDは水素、炭素、酸素、窒素原子のみからなる分子量300以下の化合物であり、すべて8員環の構造を持つ。
化合物A、Bは窒素原子を1つ含み、互いに異性体の関係にある。また、化合物C、Dは窒素原子2つを含み、互いに異性体の関係にある。
79.5 mgの化合物Aを完全燃焼させたところ、二酸化炭素205mgと水27.0mgを生じた。同様に59.5mgの化合物Cからは二酸化炭素154mgと水22.5mgを生じた。
化合物A~Dの溶液に水酸化ナトリウム水溶液を加えて加水分解を進めると、化合物E、F、G、HおよびIのような有機化合物もしくはナトリウム塩が得られた。なお、それぞれの反応生成物はAからはEとF、BからはGとH、CからはHとI、DからはEのみとなっていた。
Aを加水分解して得られた反応液に希塩酸を加えて酸性にし、ジエチルエーテルで抽出を行うと、エーテル層から化合物Fを得ることができた。
同様の操作をBの反応液に行うと、エーテル層から化合物Hを得ることができた。
化合物Eに塩酸と亜硝酸ナトリウムを加え反応させ、その後加温すると化合物Fが生成した。また、化合物Hを加熱すると脱水反応が進行した。
A~Dの構造式をかけ
【社会・日本史】卑弥呼について語ります

単元:
#社会(中学受験)#社会(中学生)#社会(高校生)#日本史#歴史#歴史#原始・古代
指導講師:
理数個別チャンネル
問題文全文(内容文):
邪馬台国はどこに?卑弥呼について語ります.
この動画を見る
邪馬台国はどこに?卑弥呼について語ります.




