 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【情報Ⅰ】シフト暗号のプログラムの問題解説

単元:
#情報Ⅰ(高校生)#プログラミング#プログラムによる動的シミュレーション
指導講師:
理数個別チャンネル
問題文全文(内容文):
第5問 次の文章を読み、後の問い(問1〜3)に答えよ。
シフト暗号はアルファベットの文字を決まった文字数分シフトさせて(ずらして)置き換える極めて単純な暗号手段である。
TさんとMさんは授業で先生が出した課題であるシフト暗号で暗号化した暗号文をいかに解読するかを考えることにした
問1 次の会話文を読み、空欄【アイ】~【キク】に当てはまる数字をマークせよ。
課題 英文をシフト暗号で暗号化した以下の暗号文を解読しなさい。ただし、英文字は全て小
文字でアルファベット以外のスペースや数字,「!」,「?」などは変換されていません。
(省略)... nonsmkdo k zybdsxy yp drkd psvon, kc k pskvk bodcsaxq zvkmo pyb
ydrc gory boqa dkfo drosb vsfo drkd ok xdkys wsgxr4 vsfo. sd sc kydaydorb
psdssdxa ksn zbyob yrdkd go crven ny drsc. led, sd vkqabo coxco, eo mkx xyd
nonsmkdo - go mkx xyd myxcombkdo - go mkx xyd rvkvvg - drsc qbyexn. dro lbkfo
wox, vsfsax kxn nokn, gry cdbeqavon robo, rkfo myxcombkdon sd, pkb k lfyfo yeb
zyyb zygob dy knn yb nodbkmd. dro gybvn gsvv vsdvod xydo, xyb vyxq bowowlob
grkd go cki robo, led sd mkx xofob pybqod grkd droi nsn robo. sd ....(省略)
Mさん:シフト暗号って,例えばアルファベットを5文字右にシフトした場合,文字「a」は文字
「f」に,文字「x」はまず2文字シフトして右端に達した後一番左端に戻り3文字シフ
トした文字「c」に置き換わるやつだよね。暗号化された文字列の復号は,その逆,つまり
左に5文字シフトすればできるよね。
Tさん:復号は必ずしも反対にシフトする必要はないよね。例えば9文字右にシフトされていた場合,
復号するには9文字左にシフトしても良いけど,右に【アイ】文字シフトすることもできるね。
図2のようにアルファベットに0〜25の番号を割り当てて考えてみると,暗号化してx番目の文字になった時,
復号はx+【アイ】の値が【ウエ】以下であればx+【アイ】番の文字に置き換わるけど,【ウエ】より大きい場合は,x+【アイ】−【オカ】番の文字に置き換えれば復号できるよね。
Mさん:暗号化で文字を何文字シフトしているか分かれば、この復号法で解読できるよね。どうやったら分かるかな。
Tさん:すべての可能性、つまり【キク】通りをプログラムで試せばいいんじゃない?
Mさん:この場合だと【キク】通りで済むけども、大文字があったり、
日本語のように文字種の数が多い言語ではとても効率が悪い方法だよ。英語であれば、単語によって文字「e」が人気があるし、逆に「z」が含まれる単語はあまり思いつかないよね。アルファベットの出現頻度を調べていればある程度推測できるんじゃないかな。インターネットで調べてみようよ。
Mさん:どうやら一般的な英文のアルファベットの出現頻度には図3のような傾向があるみたいだよ。
Tさん:文字によって出現頻度に特徴がある。暗号化された英文のアルファベットの出現頻度を調べれば、
何文字シフトされているか推測することができそうだね。1つ〜数え上げるのは大変だから数え上げるプログラムを考えてみるよ。
問2 次の会話文を読み,空欄【ケ】【コ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。また,空欄【サ】に当てはまる数字をマークせよ。
Tさん:暗号化された英文のアルファベットの出現頻度を数え上げるプログラムを図5のように考えてみたよ。このプログラムでは,配列変数Angoubunに暗号文を入れて,一文字ずつアルファベットの出現頻度を数え上げて,その結果を配列変数Hindoに入れているんだ。
Hindo[0] が a,Hindo[25] が z に対応しているよ。
(01) Angoubun = ["p","y","e","b",…(省略)…"k","b","d","r","."]
(02) 配列Hindoのすべての要素に0を代入する
(03) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(04) | bangou = 差分 【ケ】
(05) | もし bangou != -1 ならば:
(06) | 【コ】 = 【コ】 +1
(07) | 表示する(Hindo)
【関数の説明】
要素数(値)…配列の要素数を返す。
例:Data =["M","i","s","s","i","s","s","i","p","p","i"] の時
要素数(Data) は11を返す
差分(値)…アルファベットの「a」との位置の差分を返す
値がアルファベット以外の文字であれば−1を返す
例:差分("e") は4を、差分("x") は23を返す
差分("5") や 差分(",") は−1を返す
Mさん:これでアルファベットの出現頻度が調べられるよね。それで結果はどうなったの?
Tさん:このプログラムで得られた配列Hindoをグラフ化してみたよ(図6)。
Mさん:このアルファベットの出現頻度を見ると,「o」「d」「k」「y」が多いね。逆に出現頻度が
少ない「a」「h」「j」「t」も手掛かりになるね。図3と照らし合わせると,この暗号化さ
れた文字列は右に【サシ】文字シフトしていると考えられるね。
Tさん:うん,でもそれが正しいか,実際にプログラムを作って復号してみようよ。
ケ・コの解答群
| 0 Angoubun[i] | 1 Angoubun[i−1] | 2 Angoubun[bangou] |
| 3 Angoubun[bangou−1] | 4 Hindo[bangou] | 5 Hindo[bangou−1] |
| 6 Hindo[i] | 7 Hindo[i−1] |
問3 次の会話文の空欄【ス】〜【チ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。
Tさん:暗号文を一文字ずつ復号して表示するプログラムができたよ(図7)。
Mさん:なるほど、復号も右にシフトで考えればいいんだね。実行してみたら読める英文になったの?
(01) Angoubun = ["p","y","e","b",…(省略)… "k","b","d","r","."]
(02) 配列変数 Hirabun を初期化する
(03) hukugosuu = 26 - 10
(04) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(05) | bangou = 差分(Angoubun[i])
(06) | もし 0 <= bangou + 【ス】 <= 25 ならば:
(07) | Hirabun[i] = 文字( bangou + 【ス】 )
(08) | そうでなければ:
(09) | Hirabun[i] = 文字( bangou + 【セ】 )
(10) | L Hirabun[i] = 文字( 【ソ】 )
(11) そうでなければ:
(12) | L Hirabun[i] = Hirabun[i]
(13) 表示する(Hirabun)
図7 暗号文を復号するプログラム
Mさん:これって有名なリンカーンのゲティスバーグ演説じゃない。ほら最後のところ有名なフレーズだよね。
Tさん:先生、課題ができました。元の英文はリンカーンのゲティスバーグ演説ですね。プログラムで文字の出現頻度を調べて、シフトされた文字数を推測しました。復号はこのプログラムで変換してみました。
先生:よくできたね。素晴らしい!このプログラムはもっと簡単にできるね。この⑦〜⑩の部分が式は工夫すれば1行にまとめられるよ。ヒントは余りを求める算術演算子%を使うんだ。
Tさん:えっ,1行ですか? …分かった!
Hirabun[i] = 文字(【タ】 % 【チ】)
とすればもっと簡潔にできたんだ。
先生:素晴らしい!
ス〜ソ の解答群
| 0 bangou+hukugousuu | 1 bangou |
| 2 hukugousuu | 3 bangou+hukugousuu−26 |
| 4 hukugousuu−25 | 5 hukugousuu−26 |
| 6 Angoubun[i] | 7 Hirabun[i] |
| 8 Angoubun[i+hukugousuu] |
タ の解答群
| 0 bangou+hukugousuu | 1 (bangou+hukugousuu) |
| 2 hukugousuu | 3 (bangou+hukugousuu−26) |
| 4 hukugousuu+26 | 5 (hukugousuu+26) |
チ の解答群
| 0 25 | 1 26 | 2 bangou | 3 hukugousuu |
この動画を見る
第5問 次の文章を読み、後の問い(問1〜3)に答えよ。
シフト暗号はアルファベットの文字を決まった文字数分シフトさせて(ずらして)置き換える極めて単純な暗号手段である。
TさんとMさんは授業で先生が出した課題であるシフト暗号で暗号化した暗号文をいかに解読するかを考えることにした
問1 次の会話文を読み、空欄【アイ】~【キク】に当てはまる数字をマークせよ。
課題 英文をシフト暗号で暗号化した以下の暗号文を解読しなさい。ただし、英文字は全て小
文字でアルファベット以外のスペースや数字,「!」,「?」などは変換されていません。
(省略)... nonsmkdo k zybdsxy yp drkd psvon, kc k pskvk bodcsaxq zvkmo pyb
ydrc gory boqa dkfo drosb vsfo drkd ok xdkys wsgxr4 vsfo. sd sc kydaydorb
psdssdxa ksn zbyob yrdkd go crven ny drsc. led, sd vkqabo coxco, eo mkx xyd
nonsmkdo - go mkx xyd myxcombkdo - go mkx xyd rvkvvg - drsc qbyexn. dro lbkfo
wox, vsfsax kxn nokn, gry cdbeqavon robo, rkfo myxcombkdon sd, pkb k lfyfo yeb
zyyb zygob dy knn yb nodbkmd. dro gybvn gsvv vsdvod xydo, xyb vyxq bowowlob
grkd go cki robo, led sd mkx xofob pybqod grkd droi nsn robo. sd ....(省略)
Mさん:シフト暗号って,例えばアルファベットを5文字右にシフトした場合,文字「a」は文字
「f」に,文字「x」はまず2文字シフトして右端に達した後一番左端に戻り3文字シフ
トした文字「c」に置き換わるやつだよね。暗号化された文字列の復号は,その逆,つまり
左に5文字シフトすればできるよね。
Tさん:復号は必ずしも反対にシフトする必要はないよね。例えば9文字右にシフトされていた場合,
復号するには9文字左にシフトしても良いけど,右に【アイ】文字シフトすることもできるね。
図2のようにアルファベットに0〜25の番号を割り当てて考えてみると,暗号化してx番目の文字になった時,
復号はx+【アイ】の値が【ウエ】以下であればx+【アイ】番の文字に置き換わるけど,【ウエ】より大きい場合は,x+【アイ】−【オカ】番の文字に置き換えれば復号できるよね。
Mさん:暗号化で文字を何文字シフトしているか分かれば、この復号法で解読できるよね。どうやったら分かるかな。
Tさん:すべての可能性、つまり【キク】通りをプログラムで試せばいいんじゃない?
Mさん:この場合だと【キク】通りで済むけども、大文字があったり、
日本語のように文字種の数が多い言語ではとても効率が悪い方法だよ。英語であれば、単語によって文字「e」が人気があるし、逆に「z」が含まれる単語はあまり思いつかないよね。アルファベットの出現頻度を調べていればある程度推測できるんじゃないかな。インターネットで調べてみようよ。
Mさん:どうやら一般的な英文のアルファベットの出現頻度には図3のような傾向があるみたいだよ。
Tさん:文字によって出現頻度に特徴がある。暗号化された英文のアルファベットの出現頻度を調べれば、
何文字シフトされているか推測することができそうだね。1つ〜数え上げるのは大変だから数え上げるプログラムを考えてみるよ。
問2 次の会話文を読み,空欄【ケ】【コ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。また,空欄【サ】に当てはまる数字をマークせよ。
Tさん:暗号化された英文のアルファベットの出現頻度を数え上げるプログラムを図5のように考えてみたよ。このプログラムでは,配列変数Angoubunに暗号文を入れて,一文字ずつアルファベットの出現頻度を数え上げて,その結果を配列変数Hindoに入れているんだ。
Hindo[0] が a,Hindo[25] が z に対応しているよ。
(01) Angoubun = ["p","y","e","b",…(省略)…"k","b","d","r","."]
(02) 配列Hindoのすべての要素に0を代入する
(03) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(04) | bangou = 差分 【ケ】
(05) | もし bangou != -1 ならば:
(06) | 【コ】 = 【コ】 +1
(07) | 表示する(Hindo)
【関数の説明】
要素数(値)…配列の要素数を返す。
例:Data =["M","i","s","s","i","s","s","i","p","p","i"] の時
要素数(Data) は11を返す
差分(値)…アルファベットの「a」との位置の差分を返す
値がアルファベット以外の文字であれば−1を返す
例:差分("e") は4を、差分("x") は23を返す
差分("5") や 差分(",") は−1を返す
Mさん:これでアルファベットの出現頻度が調べられるよね。それで結果はどうなったの?
Tさん:このプログラムで得られた配列Hindoをグラフ化してみたよ(図6)。
Mさん:このアルファベットの出現頻度を見ると,「o」「d」「k」「y」が多いね。逆に出現頻度が
少ない「a」「h」「j」「t」も手掛かりになるね。図3と照らし合わせると,この暗号化さ
れた文字列は右に【サシ】文字シフトしていると考えられるね。
Tさん:うん,でもそれが正しいか,実際にプログラムを作って復号してみようよ。
ケ・コの解答群
| 0 Angoubun[i] | 1 Angoubun[i−1] | 2 Angoubun[bangou] |
| 3 Angoubun[bangou−1] | 4 Hindo[bangou] | 5 Hindo[bangou−1] |
| 6 Hindo[i] | 7 Hindo[i−1] |
問3 次の会話文の空欄【ス】〜【チ】に当てはまる内容を,後の解答群のうちから一つずつ選べ。
Tさん:暗号文を一文字ずつ復号して表示するプログラムができたよ(図7)。
Mさん:なるほど、復号も右にシフトで考えればいいんだね。実行してみたら読める英文になったの?
(01) Angoubun = ["p","y","e","b",…(省略)… "k","b","d","r","."]
(02) 配列変数 Hirabun を初期化する
(03) hukugosuu = 26 - 10
(04) i を 0 から 要素数(Angoubun)-1 まで1ずつ増やしながら:
(05) | bangou = 差分(Angoubun[i])
(06) | もし 0 <= bangou + 【ス】 <= 25 ならば:
(07) | Hirabun[i] = 文字( bangou + 【ス】 )
(08) | そうでなければ:
(09) | Hirabun[i] = 文字( bangou + 【セ】 )
(10) | L Hirabun[i] = 文字( 【ソ】 )
(11) そうでなければ:
(12) | L Hirabun[i] = Hirabun[i]
(13) 表示する(Hirabun)
図7 暗号文を復号するプログラム
Mさん:これって有名なリンカーンのゲティスバーグ演説じゃない。ほら最後のところ有名なフレーズだよね。
Tさん:先生、課題ができました。元の英文はリンカーンのゲティスバーグ演説ですね。プログラムで文字の出現頻度を調べて、シフトされた文字数を推測しました。復号はこのプログラムで変換してみました。
先生:よくできたね。素晴らしい!このプログラムはもっと簡単にできるね。この⑦〜⑩の部分が式は工夫すれば1行にまとめられるよ。ヒントは余りを求める算術演算子%を使うんだ。
Tさん:えっ,1行ですか? …分かった!
Hirabun[i] = 文字(【タ】 % 【チ】)
とすればもっと簡潔にできたんだ。
先生:素晴らしい!
ス〜ソ の解答群
| 0 bangou+hukugousuu | 1 bangou |
| 2 hukugousuu | 3 bangou+hukugousuu−26 |
| 4 hukugousuu−25 | 5 hukugousuu−26 |
| 6 Angoubun[i] | 7 Hirabun[i] |
| 8 Angoubun[i+hukugousuu] |
タ の解答群
| 0 bangou+hukugousuu | 1 (bangou+hukugousuu) |
| 2 hukugousuu | 3 (bangou+hukugousuu−26) |
| 4 hukugousuu+26 | 5 (hukugousuu+26) |
チ の解答群
| 0 25 | 1 26 | 2 bangou | 3 hukugousuu |
【数Ⅰ】【2次関数】グラフを利用して、次の不等式を解け。(1) |x+1|<2x (2) |x²-4| >-3x

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
この動画を見る
グラフを利用して、次の不等式を解け。
(1) |x+1|<2x
(2) |x²-4| >-3x
【受験算数】A地点から峠をこえてB地点まで往復。上り道は時速3.6km、下り道は時速7.2kmで歩く人が行きは10時間50分かかってB地点へ帰りは9時間10分かかってA地点へ。A地点から峠までの距離は

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点から峠をこえてB地点まで往復する。上り道は時速3.6km、下り道は時速7.2kmで歩く人が、行きは10時間50分かかってB地点に着き、帰りは9時間10分かかってA地点に着いた。A地点から峠までの距離は何kmか。ただし、平地はない。
この動画を見る
A地点から峠をこえてB地点まで往復する。上り道は時速3.6km、下り道は時速7.2kmで歩く人が、行きは10時間50分かかってB地点に着き、帰りは9時間10分かかってA地点に着いた。A地点から峠までの距離は何kmか。ただし、平地はない。
【高校物理】核分裂:ウランUの原子核に中性子nを衝突させると、バリウムBaとクリプトンKrの原子核に分裂し、同時に3つの中性子が生じた。次の各問に答えよ。ただし、各原子核の質量は…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
ウランUの原子核に中性子nを衝突させると、バリウムBaとクリプトンKrの原子核に分裂し、同時に3つの中性子が生じた。次の各問に答えよ。ただし、各原子核の質量は、Uが234.9935u、Ba が140.8837u、Krが91.9074uであり、nが1.0087uであるとする。また1u = 1.66×10kg、真空中の光速をc=3.00×10m/s、電気素量をe=1.60×10Cとする。
(1) この核分裂の核反応式を示せ。
(2) 核反応における質量の減少は何uか。また、それは何kgか。
(3) 核反応がおこったときに発生するエネルギーは何Jか。また、それは何MeVか。
(4) ウランUの原子核4.70gが全てこの核分裂をおこしたとすると、何Jのエネルギーが放出されるか。
この動画を見る
ウランUの原子核に中性子nを衝突させると、バリウムBaとクリプトンKrの原子核に分裂し、同時に3つの中性子が生じた。次の各問に答えよ。ただし、各原子核の質量は、Uが234.9935u、Ba が140.8837u、Krが91.9074uであり、nが1.0087uであるとする。また1u = 1.66×10kg、真空中の光速をc=3.00×10m/s、電気素量をe=1.60×10Cとする。
(1) この核分裂の核反応式を示せ。
(2) 核反応における質量の減少は何uか。また、それは何kgか。
(3) 核反応がおこったときに発生するエネルギーは何Jか。また、それは何MeVか。
(4) ウランUの原子核4.70gが全てこの核分裂をおこしたとすると、何Jのエネルギーが放出されるか。
【受験算数】A地点から峠をこえてB地点まで往復する。上り道は時速4km、下り道は時速6kmで歩く人が行きは9時間40分かかってB地点へ、帰りは10時間20分かかってA地点へ。A地点から峠までの距離は?

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点から峠をこえてB地点まで往復する。上り道は時速4km、下り道は時速6kmで歩く人が、行きは9時間40分かかってB地点に着き、帰りは10時間20分かかってA地点に着いた。A地点から峠までの距離は何kmか。ただし、平地はない。
この動画を見る
A地点から峠をこえてB地点まで往復する。上り道は時速4km、下り道は時速6kmで歩く人が、行きは9時間40分かかってB地点に着き、帰りは10時間20分かかってA地点に着いた。A地点から峠までの距離は何kmか。ただし、平地はない。
【数Ⅰ】【2次関数】x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
この動画を見る
x,yがお互いに関係なく変化するとき、Z=x²ー6xy+y²+2yの最小値を求めよ。
【中学受験理科】燃焼①:グラフは、いろいろな重さの銅とマグネシウムを完全に燃やしたときに何gになるかを調べてまとめたものです。問1 24gの銅とマグネシウムを完全に燃やすと、それぞれ何gになりますか…

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフは、いろいろな重さの銅とマグネシウムを完全に燃やしたときに何gになるかを調べてまとめたものです。
問1 24gの銅とマグネシウムを完全に燃やすと、それぞれ何gになりますか。
問2 18gの酸化マグネシウムをつくるには、何gのマグネシウムが必要ですか。
問3 一定量の酸素と結びつく銅とマグネシウムの重さを、最も簡単な整数の比で答えなさい。
問4 銅粉末12gとマグネシウム粉末9gを混ぜた21gの粉末を、完全に燃やすためには何gの酸素が必要ですか。
問5 銅粉末とマグネシウム粉末が合わせて30gあります。この粉末を完全に燃やすと、45gになりました。マグネシウム粉末は何gありましたか。
1.2gのマグネシウムの粉末をステンレス製の皿の上にのせて、ガスバーナーでステンレスの皿ごと2分間加熱します。完全に冷えてから粉末の重さをはかると、1.7gでした。「加熱→冷却→重さをはかる」を5回くり返して、結果をまとめたものが下の表です。
問6 マグネシウムが完全に酸素と結びついたのは、何回目の加熱ですか。
問7 1回加熱したとき、酸素は何g結びつきましたか。
問8 2回加熱したとき、まだ酸素と結びついていないマグネシウムは何8残っていますか。
この動画を見る
グラフは、いろいろな重さの銅とマグネシウムを完全に燃やしたときに何gになるかを調べてまとめたものです。
問1 24gの銅とマグネシウムを完全に燃やすと、それぞれ何gになりますか。
問2 18gの酸化マグネシウムをつくるには、何gのマグネシウムが必要ですか。
問3 一定量の酸素と結びつく銅とマグネシウムの重さを、最も簡単な整数の比で答えなさい。
問4 銅粉末12gとマグネシウム粉末9gを混ぜた21gの粉末を、完全に燃やすためには何gの酸素が必要ですか。
問5 銅粉末とマグネシウム粉末が合わせて30gあります。この粉末を完全に燃やすと、45gになりました。マグネシウム粉末は何gありましたか。
1.2gのマグネシウムの粉末をステンレス製の皿の上にのせて、ガスバーナーでステンレスの皿ごと2分間加熱します。完全に冷えてから粉末の重さをはかると、1.7gでした。「加熱→冷却→重さをはかる」を5回くり返して、結果をまとめたものが下の表です。
問6 マグネシウムが完全に酸素と結びついたのは、何回目の加熱ですか。
問7 1回加熱したとき、酸素は何g結びつきましたか。
問8 2回加熱したとき、まだ酸素と結びついていないマグネシウムは何8残っていますか。
【高校物理】核分裂とエネルギー:1.0kgのウランがすべて核分裂をすると、8.4×10kgの質量がエネルギーに変わる。出力2.1×10kWの原子炉があるとする。真空中の光速を3.0×10m/sとし、…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
1.0kgのウランがすべて核分裂をすると、8.4×10kgの質量がエネルギーに変わる。出力2.1×10kWの原子炉があるとする。真空中の光速を3.0×10m/sとし、エネルギーの損失は無視できるとして、次の各問に答えよ。
(1) 原子炉内で、ウランは毎時何kgずつ核分裂をおこしているか。
(2) このエネルギーを出すには、発熱量3.0×10J/kgの石炭を毎時何kg必要とするか。
この動画を見る
1.0kgのウランがすべて核分裂をすると、8.4×10kgの質量がエネルギーに変わる。出力2.1×10kWの原子炉があるとする。真空中の光速を3.0×10m/sとし、エネルギーの損失は無視できるとして、次の各問に答えよ。
(1) 原子炉内で、ウランは毎時何kgずつ核分裂をおこしているか。
(2) このエネルギーを出すには、発熱量3.0×10J/kgの石炭を毎時何kg必要とするか。
【受験算数】 A地点からB地点までは平地で、C地点は山頂。Aから出発してA、C間を往復するのに行きは3時間30分、帰りは2時間45分。平地は時速4.8km、上りは時速3.6km、下りは時速5.4km

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは3時間30分、帰りは2時間45分かかった。平地は時速4.8km、上りは時速3.6km、下りは時速5.4kmで歩いた。
(1)B、C間の距離は何kmか。(2)A、B間の距離は何kmか。
この動画を見る
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは3時間30分、帰りは2時間45分かかった。平地は時速4.8km、上りは時速3.6km、下りは時速5.4kmで歩いた。
(1)B、C間の距離は何kmか。(2)A、B間の距離は何kmか。
【数Ⅰ】【2次関数】x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
この動画を見る
x²+y²=1 のときx²ーy²+2xの最大値と最小値を求めよ。
【中学受験理科】月の満ち欠け②:次の図は、地球の北極側から月を見た様子です。また、表はある年の12月17日~12月30日の、月の出、月の入の時刻を表しています。問1 12月20日の月はA~Hのどの位…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の図は、地球の北極側から月を見た様子です。また、表はある年の12月17日~12月30日の、月の出、月の入の時刻を表しています。
問1 12月20日の月はA~Hのどの位置にある月ともっとも近いですか
問2 12月20日に出た月が出ていた時間は何時間何分ですか
問3 12月25日に出た月が出ていた時間は何時間何分ですか
※表や図は動画内に記載
この動画を見る
次の図は、地球の北極側から月を見た様子です。また、表はある年の12月17日~12月30日の、月の出、月の入の時刻を表しています。
問1 12月20日の月はA~Hのどの位置にある月ともっとも近いですか
問2 12月20日に出た月が出ていた時間は何時間何分ですか
問3 12月25日に出た月が出ていた時間は何時間何分ですか
※表や図は動画内に記載
【高校物理】結合エネルギー:図は、核子1個あたりの結合エネルギーを縦軸に、質量数を横軸にとったグラフである。(1)Li と Cはどちらが安定な原子核か。(2)He の核子1個あたりの結合エネルギーは…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、核子1個あたりの結合エネルギーを縦軸に、質量数を横軸にとったグラフである。
(1)Li と Cはどちらが安定な原子核か。
(2)He の核子1個あたりの結合エネルギーは2.5MeVと読み取れる。Heの原子核の結合エネルギーは何MeVか。
(3) 質量数の小さい水素では核融合がおこり、質量数の大きいウランでは核分裂がおこる。その理由を簡潔に説明せよ。
この動画を見る
図は、核子1個あたりの結合エネルギーを縦軸に、質量数を横軸にとったグラフである。
(1)Li と Cはどちらが安定な原子核か。
(2)He の核子1個あたりの結合エネルギーは2.5MeVと読み取れる。Heの原子核の結合エネルギーは何MeVか。
(3) 質量数の小さい水素では核融合がおこり、質量数の大きいウランでは核分裂がおこる。その理由を簡潔に説明せよ。
【受験算数】 A地点からB地点までは平地でC地点は山頂。Aから出発してA、C間を往復するのに行きは2時間42分、帰りは2時間18分かかった。平地は時速5km、上りは時速4km、下りは時速6kmで歩いた

単元:
#算数(中学受験)#速さ#速さその他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは2時間42分、帰りは2時間18分かかった。平地は時速5km、上りは時速4km、下りは時速6kmで歩いた。
(1)B、C間の距離は何kmか。 (2)A、B間の距離は何kmか。
この動画を見る
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは2時間42分、帰りは2時間18分かかった。平地は時速5km、上りは時速4km、下りは時速6kmで歩いた。
(1)B、C間の距離は何kmか。 (2)A、B間の距離は何kmか。
【数Ⅰ】【データの分析】672、693、644、665、630、644でc=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。変量uとxの平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量xのデータが次のように与えられている。
672,693、644、665、630、644
c=7、x₀=644、u=(x-x₀)/c として新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
【高校物理】結合エネルギー:三重水素Hの原子核は、陽子1個、中性子2個からなり、それぞれの1個あたりの質量は、5.008 × 10kg、1.673 × 10kg、1.675 × 10kg である。次…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
三重水素Hの原子核は、陽子1個、中性子2個からなり、それぞれの1個あたりの質量は、5.008 × 10kg、1.673 × 10kg、1.675 × 10kg である。次の各問に答えよ。ただし、真空中の光速を3.0 × 10m/s とする。
(1) 三重水素Hの原子核の質量欠損は何kgか。また、結合エネルギーは何Jか。
(2) 核子1個あたりの結合エネルギーは何Jか。
この動画を見る
三重水素Hの原子核は、陽子1個、中性子2個からなり、それぞれの1個あたりの質量は、5.008 × 10kg、1.673 × 10kg、1.675 × 10kg である。次の各問に答えよ。ただし、真空中の光速を3.0 × 10m/s とする。
(1) 三重水素Hの原子核の質量欠損は何kgか。また、結合エネルギーは何Jか。
(2) 核子1個あたりの結合エネルギーは何Jか。
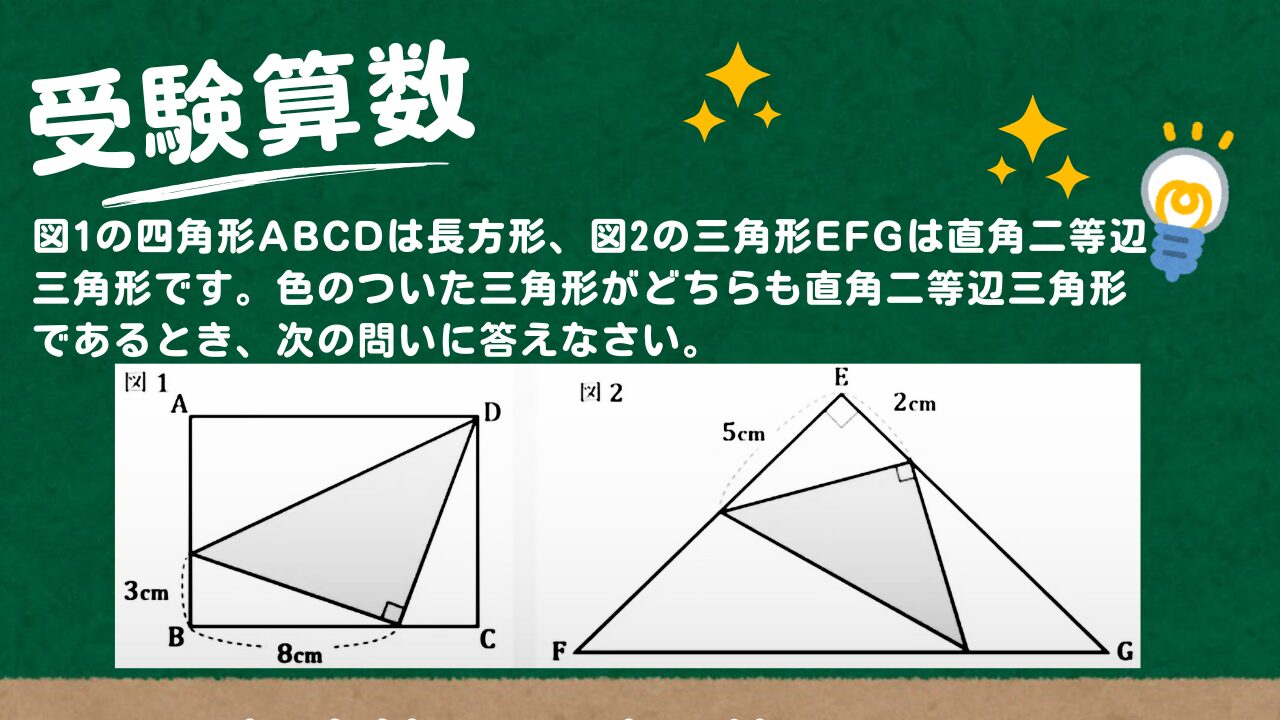
【受験算数】図1の四角形ABCDは長方形、図2の三角形EFGは直角二等辺三角形です。色のついた三角形がどちらも直角二等辺三角形であるとき、次の問いに答えなさい。
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1の四角形ABCDは長方形、図2の三角形EFGは直角二等辺三角形です。色のついた三角形がどちらも直角二等辺三角形であるとき、次の問いに答えなさい。
この動画を見る
図1の四角形ABCDは長方形、図2の三角形EFGは直角二等辺三角形です。色のついた三角形がどちらも直角二等辺三角形であるとき、次の問いに答えなさい。
【数Ⅰ】【データの分析】あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。生徒全員の得点を2.5倍して、30点を加えたとき、平均値、分散、標準偏差を求めよ。

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
この動画を見る
あるクラスの生徒を対象に100点満点の試験を行ったところ、平均値は68点、分散は36であった。得点調整のため、生徒全員の得点を2.5倍して、更に30点を加えたとき、得点調整後の平均値、分散、標準偏差を求めよ。
【中学受験理科】月の満ち欠け:次の図は、地球の北極側から月を見た様子です。日本で見られる月について、次の問に答えなさい。問1 月が図1のように見えるのは、月がA~Hのどの位置にあるときですか。それぞ…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の図は、地球の北極側から月を見た様子です。日本で見られる月について、次の問に答えなさい。
問1 月が図1のように見えるのは、月がA~Hのどの位置にあるときですか。それぞれ選びなさい
問2 A,B,Fの月の南中時刻はそれぞれ何時ごろですか。次のア~クから選びなさい
ア 午前0時 イ 午前3時 ウ 午前6時 エ 午前9時
オ 正午 カ 午後3時 キ 午後6時 ク 午後9時
問3 日食と月食が見られるときの月はA~Hのどれですか。それぞれ選びなさい
問4 大潮と小潮が見られるときの月は月はA~Hのどれですか。それぞれ選びなさい
※表や図は動画内に記載
この動画を見る
次の図は、地球の北極側から月を見た様子です。日本で見られる月について、次の問に答えなさい。
問1 月が図1のように見えるのは、月がA~Hのどの位置にあるときですか。それぞれ選びなさい
問2 A,B,Fの月の南中時刻はそれぞれ何時ごろですか。次のア~クから選びなさい
ア 午前0時 イ 午前3時 ウ 午前6時 エ 午前9時
オ 正午 カ 午後3時 キ 午後6時 ク 午後9時
問3 日食と月食が見られるときの月はA~Hのどれですか。それぞれ選びなさい
問4 大潮と小潮が見られるときの月は月はA~Hのどれですか。それぞれ選びなさい
※表や図は動画内に記載
【高校物理】レンズのコーティング:めがねのレンズは、光の反射をおさえるために、表面に薄膜がつけられている。屈折率1.8のレンズの表面に、それよりも小さい屈折率n(>1)の薄膜をつけ,波長λの光を垂直…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
めがねのレンズは、光の反射をおさえるために、表面に薄膜がつけられている。屈折率1.8のレンズの表面に、それよりも小さい屈折率n(>1)の薄膜をつけ,波長λの光を垂直に入射させる。m=0,1,2,・・・として、次の各問に答えよ。
(1) 光は、図の点A〜Dでそれぞれ反射する。反射によって光の位相はずれるか,ずれないか。それぞれ答えよ。
(2) 反射光が弱めあっているとき、薄膜の厚さdを、n,λ,mを用いて表せ。
(3) (2)のとき、薄膜を透過する光は強めあっているか、弱めあっているか。
(4) n=1.4,λ=5.6✕10-3mのとき、透過が強めあう最小のdを求めよ。
この動画を見る
めがねのレンズは、光の反射をおさえるために、表面に薄膜がつけられている。屈折率1.8のレンズの表面に、それよりも小さい屈折率n(>1)の薄膜をつけ,波長λの光を垂直に入射させる。m=0,1,2,・・・として、次の各問に答えよ。
(1) 光は、図の点A〜Dでそれぞれ反射する。反射によって光の位相はずれるか,ずれないか。それぞれ答えよ。
(2) 反射光が弱めあっているとき、薄膜の厚さdを、n,λ,mを用いて表せ。
(3) (2)のとき、薄膜を透過する光は強めあっているか、弱めあっているか。
(4) n=1.4,λ=5.6✕10-3mのとき、透過が強めあう最小のdを求めよ。
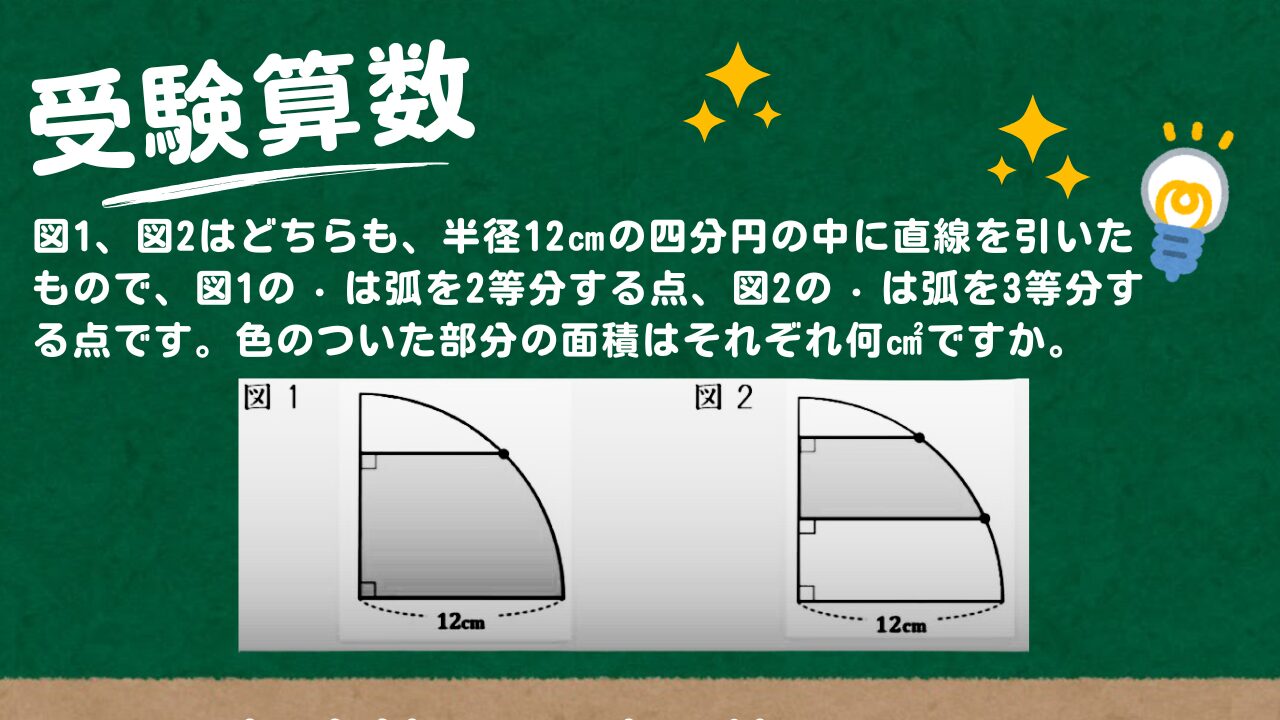
【受験算数】図1、図2はどちらも、半径12㎝の四分円の中に直線を引いたもので、図1の · は弧を2等分する点、図2の · は弧を3等分する点です。色のついた部分の面積はそれぞれ何㎠ですか。
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1、図2はどちらも、半径12㎝の四分円の中に直線を引いたもので、図1の · は弧を2等分する点、図2の · は弧を3等分する点です。色のついた部分の面積はそれぞれ何㎠ですか。
この動画を見る
図1、図2はどちらも、半径12㎝の四分円の中に直線を引いたもので、図1の · は弧を2等分する点、図2の · は弧を3等分する点です。色のついた部分の面積はそれぞれ何㎠ですか。
【数Ⅰ】【データの分析】変量Xのデータの平均値xが35、分散Sx²が16で新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ(1)y=x-10(2)y=3x(3)y=-x/2+6

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
この動画を見る
変量Xのデータの平均値xが35、分散Sx²が16であるとする。
このとき、次の式によってえられる新しい変量Yのデータについて、平均値y、分散Sy²、標準偏差Syを求めよ。
(1)y=x-10
(2)y=3x
(3)y=-x/2+6
【中学受験理科】透明半球上の太陽の動き:よく晴れた日に、透明半球を使って太陽の動きを調べました(図1)。午前8時から観測をはじめ、1時間おきにア~オの順にサインペンで印をつけました(図2)。…

単元:
#理科(中学受験)#地学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
よく晴れた日に、透明半球を使って太陽の動きを調べました(図1)。午前8時から観測をはじめ、1時間おきにア~オの順にサインペンで印をつけました(図2)。
この点を滑らかな線で結び、透明半球のふちとぶつかった点をOとします。つまり、Q点が日の出というわけです。また天頂(真上)をT点とし、TとR(真南)も滑らかな線で結びました。
表は、Q点からそれぞれの点までの長さをまとめたものです。この観測に対して、次の問に答えなさい。
問1 この日の日の出は何時何分ですか。24時間制で答えなさい
問2 この日の南中時刻は11時45分でした。xにあてはまる数を求めなさい
問3 RからP、Tまでの半球上の長さをそれぞれ80mm、150mmとすると、この日の南中高度は何度になりますか
※表や図は動画内に記載"
この動画を見る
よく晴れた日に、透明半球を使って太陽の動きを調べました(図1)。午前8時から観測をはじめ、1時間おきにア~オの順にサインペンで印をつけました(図2)。
この点を滑らかな線で結び、透明半球のふちとぶつかった点をOとします。つまり、Q点が日の出というわけです。また天頂(真上)をT点とし、TとR(真南)も滑らかな線で結びました。
表は、Q点からそれぞれの点までの長さをまとめたものです。この観測に対して、次の問に答えなさい。
問1 この日の日の出は何時何分ですか。24時間制で答えなさい
問2 この日の南中時刻は11時45分でした。xにあてはまる数を求めなさい
問3 RからP、Tまでの半球上の長さをそれぞれ80mm、150mmとすると、この日の南中高度は何度になりますか
※表や図は動画内に記載"
【高校物理】光学距離:屈折率n、厚さのdの透明な平板がある。真空中で波長λの光が、この平板に垂直に入射して透過する。このとき、次の各問に答えよ。(1) 平板の厚さに相当する光学距離を求めよ。(2) …

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
屈折率n、厚さのdの透明な平板がある。真空中で波長λの光が、この平板に垂直に入射して透過する。このとき、次の各問に答えよ。
(1) 平板の厚さに相当する光学距離を求めよ。
(2) 真空中の光速をcとして、平板中を光が進む時間を光学距離から求めよ。
この動画を見る
屈折率n、厚さのdの透明な平板がある。真空中で波長λの光が、この平板に垂直に入射して透過する。このとき、次の各問に答えよ。
(1) 平板の厚さに相当する光学距離を求めよ。
(2) 真空中の光速をcとして、平板中を光が進む時間を光学距離から求めよ。
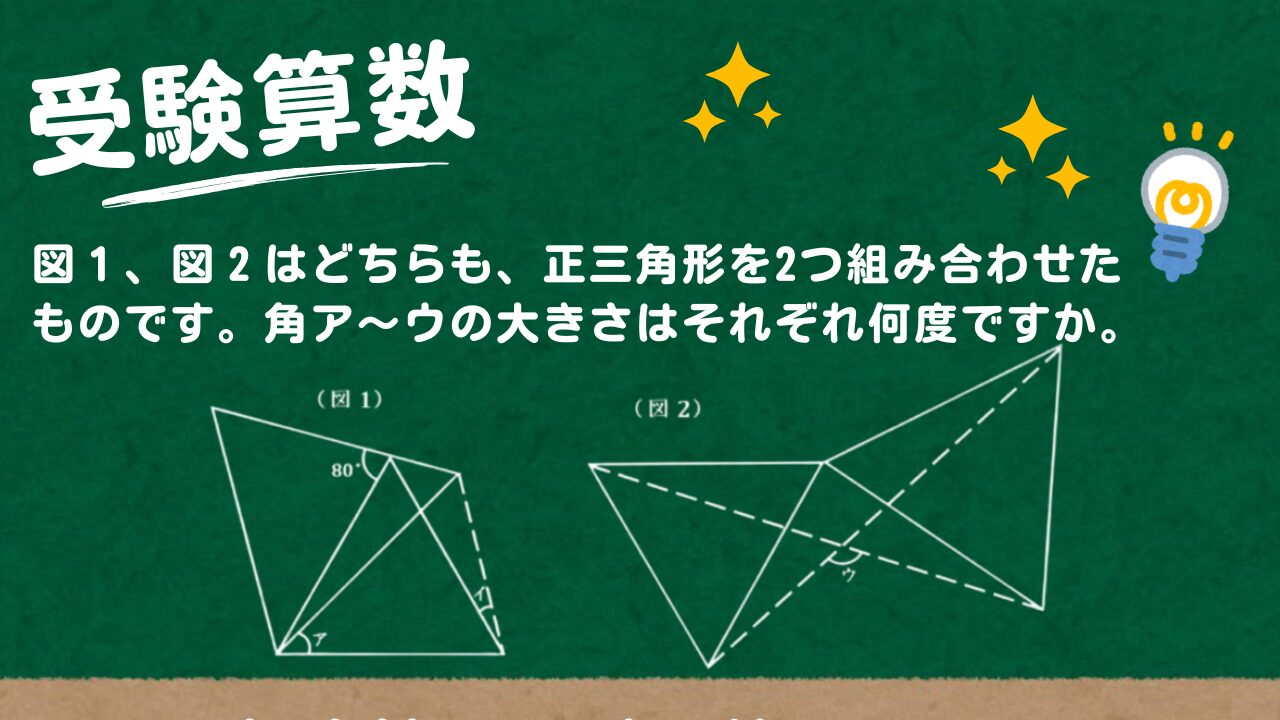
【受験算数】図1、図2はどちらも、正三角形を2つ組み合わせたものです。角ア~ウの大きさはそれぞれ何度ですか。
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1、図2はどちらも、正三角形を2つ組み合わせたものです。角ア~ウの大きさはそれぞれ何度ですか。
この動画を見る
図1、図2はどちらも、正三角形を2つ組み合わせたものです。角ア~ウの大きさはそれぞれ何度ですか。
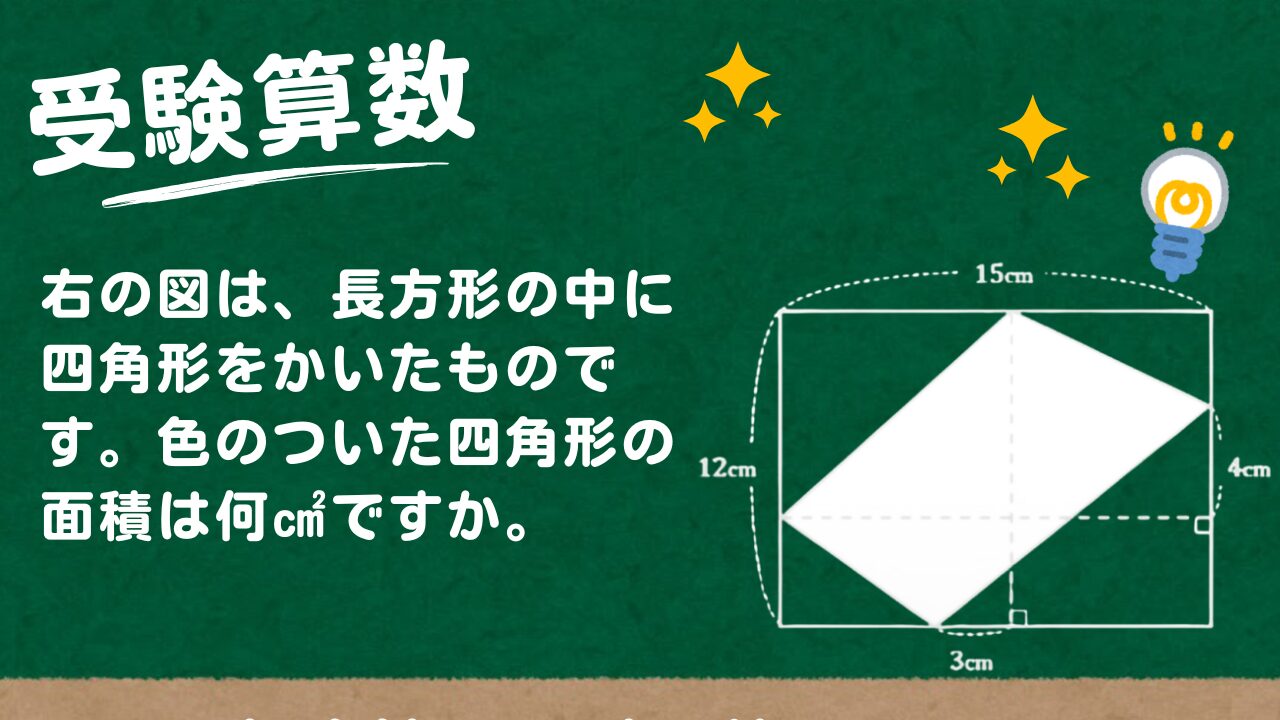
【受験算数】右の図は、長方形の中に四角形をかいたものです。色のついた四角形の面積は何㎠ですか。
単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、長方形の中に四角形をかいたものです。色のついた四角形の面積は何㎠ですか。
この動画を見る
右の図は、長方形の中に四角形をかいたものです。色のついた四角形の面積は何㎠ですか。
【数Ⅰ】【2次関数】次の条件を満たすような定数a の値の範囲を求めよ。(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。他1問

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
この動画を見る
次の条件を満たすような定数a の値の範囲を求めよ。
(1) 二次方程式 2x²-3x+a=0 の1つの解が 0<x<1 の範囲にあり、他の解が 0<x<1 の範囲にある。
(2) 二次方程式 2ax²-(a+2)x-5=0 の1つの解が -1<x<0 の範囲にあり、他の解が 2<x<3 の範囲にある。ただし a>0 とする。
【数Ⅰ】【2次関数】a<b<c のとき(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0の2つの解のうち1つは a<x<b の範囲にありもう1つは b<x<c の範囲にあることを示せ

【受験算数】右の図は、正方形ABCDの中に正方形EFGHをかき、さらにその中に四分円をかいたものです。(1)正方形EFGHの面積は何㎠ですか。(2)色のついた四分円の面積は何㎠ですか。

単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、正方形ABCDの中に正方形EFGHをかき、さらにその中に四分円をかいたものです。これについて、次の問いに答えなさい。
(1)正方形EFGHの面積は何㎠ですか。
(2)色のついた四分円の面積は何㎠ですか。
この動画を見る
右の図は、正方形ABCDの中に正方形EFGHをかき、さらにその中に四分円をかいたものです。これについて、次の問いに答えなさい。
(1)正方形EFGHの面積は何㎠ですか。
(2)色のついた四分円の面積は何㎠ですか。
【高校物理】磁場中を回転する導体棒:図のように、鉛直下向きに磁束密度 B[T] の一様な磁場中で、長さ [m]の導体棒 OP を、O を中心として水平面内で回転させる。棒 OP の角速度は ω[ra…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、鉛直下向きに磁束密度 B[T] の一様な磁場中で、長さ [m]の導体棒 OP を、O を中心として水平面内で回転させる。棒 OP の角速度は ω[rad/s] である。
(1) 点 O と P のどちらの電位が高いか。
(2) OP 間の誘導起電力の大きさはいくらか。
この動画を見る
図のように、鉛直下向きに磁束密度 B[T] の一様な磁場中で、長さ [m]の導体棒 OP を、O を中心として水平面内で回転させる。棒 OP の角速度は ω[rad/s] である。
(1) 点 O と P のどちらの電位が高いか。
(2) OP 間の誘導起電力の大きさはいくらか。
【受験算数】右の図は、四角形の中に直線を2本ひいたもので、四角形ABCDの面積は105㎠、三角形ACDの面積は42㎠です。(1)ADの長さは何㎝ですか。(2)BFの長さは何㎝ですか。

単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、四角形の中に直線を2本ひいたもので、四角形ABCD
の面積は105㎠、三角形ACDの面積は42㎠です。これについて、次の問いに答えなさい。
(1)ADの長さは何㎝ですか。
(2)BFの長さは何㎝ですか。
この動画を見る
右の図は、四角形の中に直線を2本ひいたもので、四角形ABCD
の面積は105㎠、三角形ACDの面積は42㎠です。これについて、次の問いに答えなさい。
(1)ADの長さは何㎝ですか。
(2)BFの長さは何㎝ですか。




