 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅰ】【2次関数】放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
この動画を見る
放物線 y=x²-4x+2 と直瀬 y=2x+k が接するとき、定数k の値を求めよ。またそのときの接点の座標を求めよ。
【数Ⅰ】【2次関数】放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
この動画を見る
放物線 y=x² と直線 y=-2x+k の共有点の個数は定数k の値によりどのように変化するか。
【中学受験理科】浮力⑥:図1のように、台はかりの上に300gの水そうを置き、水を500g入れました。図2の状態から ある物体を下げていき、ばねはかりの示す値を調べたところ、グラフのようになりました。…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のように、台はかりの上に300gの水そうを置き、水を500g入れました。図2の状態から ある物体を下げていき、ばねはかりの示す値を調べたところ、グラフのようになりました。なお、水 1cm³の重さは1gとします。
問1 物体の空気中での重さは何gですか。
問2 物体の体積は何cm³ ですか。
問3 物体を1.5cm下げたとき、台はかりは何gを示しますか。
問4 物体が水そうの底についたとき、物体をつるしていた糸がたるみました。このとき、台はかりは何gを示しますか。
問5 物体が水そうの底についたとき、水の深さは何cmになりますか。
この動画を見る
図1のように、台はかりの上に300gの水そうを置き、水を500g入れました。図2の状態から ある物体を下げていき、ばねはかりの示す値を調べたところ、グラフのようになりました。なお、水 1cm³の重さは1gとします。
問1 物体の空気中での重さは何gですか。
問2 物体の体積は何cm³ ですか。
問3 物体を1.5cm下げたとき、台はかりは何gを示しますか。
問4 物体が水そうの底についたとき、物体をつるしていた糸がたるみました。このとき、台はかりは何gを示しますか。
問5 物体が水そうの底についたとき、水の深さは何cmになりますか。
【受験算数】半径1cmの円が、右の図の三角形のまわりにそって転がりながら1周してもとの位置にもどります。円の中心が動いたあとの線の長さは何cmですか。

単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径1cmの円が、右の図の三角形のまわりにそって転がりながら1周してもとの位置にもどります。
これについて、次の問いに答えなさい。
(1) 円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。
この動画を見る
半径1cmの円が、右の図の三角形のまわりにそって転がりながら1周してもとの位置にもどります。
これについて、次の問いに答えなさい。
(1) 円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。
【高校物理】X線の発生とスペクトル:X線管において,初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を1.6✕10^-19C,…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
X線管において,初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を1.6✕10^-19C,プランク定数を6.6✕10^-34J・S,真空中の光速を3.0✕10^8m/sとする。次の各問に答えよ。
(1) 加速された電子のもつエネルギーは何eVか。
(2) 連続X線の最短波長はいくらか。
(3) 加速電圧を3倍にしたとき、次の値は何倍になるか。
①連続X線の最短波長 ②特性X線の波長
この動画を見る
X線管において,初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を1.6✕10^-19C,プランク定数を6.6✕10^-34J・S,真空中の光速を3.0✕10^8m/sとする。次の各問に答えよ。
(1) 加速された電子のもつエネルギーは何eVか。
(2) 連続X線の最短波長はいくらか。
(3) 加速電圧を3倍にしたとき、次の値は何倍になるか。
①連続X線の最短波長 ②特性X線の波長
【受験算数】半径1cmの円が、右の図のおうぎ形のまわりにそって 1周してもとの位置にもどります。(1) 円の中心が動いたあとの線の長さは何cmですか。(2) 円が動いたあとの図形の面積は何cm²ですか

単元:
#算数(中学受験)#平面図形#平面図形その他
教材:
#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径1cmの円が、右の図のおうぎ形のまわりにそって 1周してもとの位置にもどります。これについて、次の問いに答えなさい。
(1) 円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。
この動画を見る
半径1cmの円が、右の図のおうぎ形のまわりにそって 1周してもとの位置にもどります。これについて、次の問いに答えなさい。
(1) 円の中心が動いたあとの線の長さは何cmですか。
(2) 円が動いたあとの図形の面積は何cm²ですか。
【数Ⅰ】【2次関数】次の関数に最大値・最小値があればそれを求めよ。(1) y=-2x⁴+4x²+3(2) y=(x²-2x)²+4(x²-2x)-1

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#2次関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
この動画を見る
次の関数に最大値・最小値があればそれを求めよ。
(1) y=-2x⁴+4x²+3
(2) y=(x²-2x)²+4(x²-2x)-1
【中学受験理科】浮力⑤:次の図のような円すい形のおもりを水にしずめ、ばねはかりや台はかりが示す値を調べました。水1cm³の重さは1gであるとして、次の問いに答えなさい。問1 図1のとき、ばねはかりと…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の図のような円すい形のおもりを水にしずめ、ばねはかりや台はかりが示す値を調べました。
水1cm³の重さは1gであるとして、次の問いに答えなさい。
問1 図1のとき、ばねはかりと台はかりは何gを示しますか。
問2 図2のとき、ばねはかりと台はかりは何gを示しますか。
問3 図3のとき、ばねはかりと台はかりは何gを示しますか。
この動画を見る
次の図のような円すい形のおもりを水にしずめ、ばねはかりや台はかりが示す値を調べました。
水1cm³の重さは1gであるとして、次の問いに答えなさい。
問1 図1のとき、ばねはかりと台はかりは何gを示しますか。
問2 図2のとき、ばねはかりと台はかりは何gを示しますか。
問3 図3のとき、ばねはかりと台はかりは何gを示しますか。
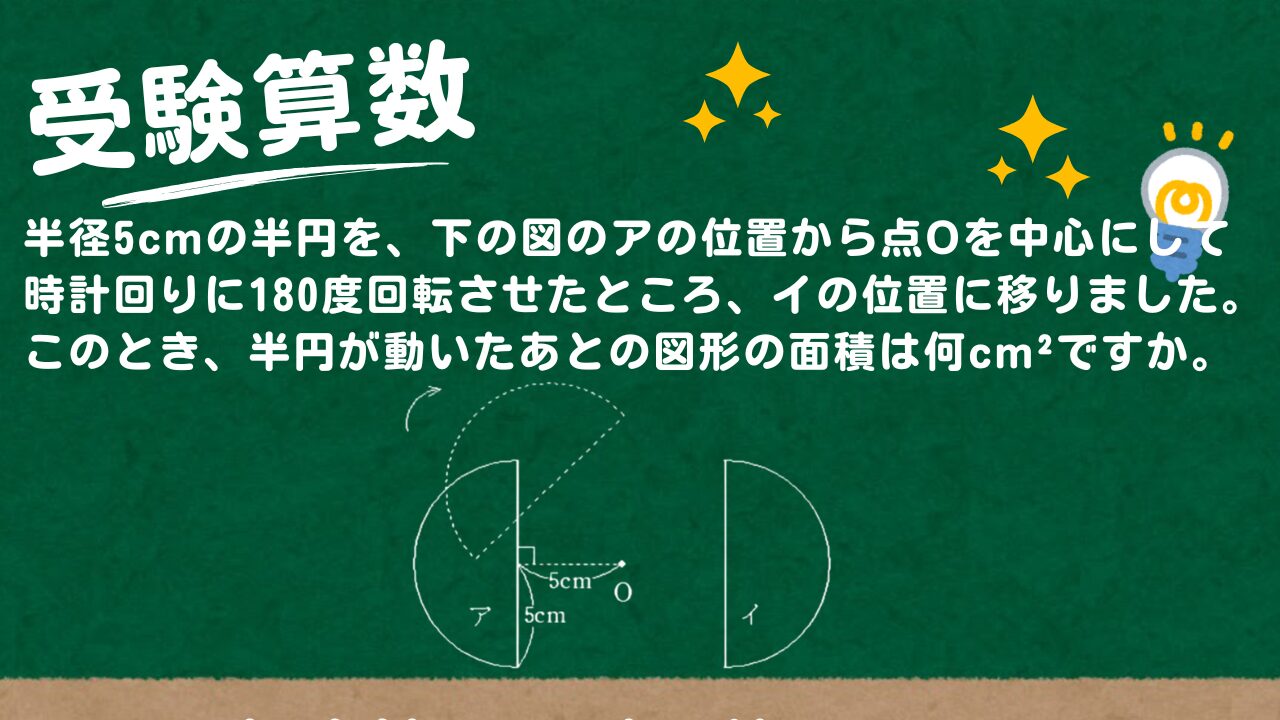
【受験算数】半径5cmの半円を、下の図のアの位置から点Oを中心にして時計回りに180度回転させたところ、イの位置に移りました。このとき、半円が動いたあとの図形の面積は何cm²ですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径5cmの半円を、下の図のアの位置から点Oを中心にして時計回りに180度回転させたところ、イの位置に移りました。
このとき、半円が動いたあとの図形の面積は何cm²ですか
この動画を見る
半径5cmの半円を、下の図のアの位置から点Oを中心にして時計回りに180度回転させたところ、イの位置に移りました。
このとき、半円が動いたあとの図形の面積は何cm²ですか
【高校物理】X線の発生:光電効果の実験で、光電管の陰極に振動数νの光をあて、光電流が0になるときの陰極に対する陽極の電位-VMを測定すると、図の関係が得られた。光電子は振動数がν0をこえたときにだけ…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のようなX線管で,陰極から初速度0で出た電子が、電位差V[V]で加速されて陽極に衝突した。次の各問に答えよ。ただし、電子の電荷を一e[C],質量をm[kg],プランク定数をh[J・s],真空中の光速をc[cm/s]とする。
(1)陽極に衝突するときの電子の運動エネルギーを求めよ。
(2)発生するX線の最短波長を求めよ。
(3)加速電圧を2倍にすると、最短波長は何倍になるか。
この動画を見る
図のようなX線管で,陰極から初速度0で出た電子が、電位差V[V]で加速されて陽極に衝突した。次の各問に答えよ。ただし、電子の電荷を一e[C],質量をm[kg],プランク定数をh[J・s],真空中の光速をc[cm/s]とする。
(1)陽極に衝突するときの電子の運動エネルギーを求めよ。
(2)発生するX線の最短波長を求めよ。
(3)加速電圧を2倍にすると、最短波長は何倍になるか。
【受験算数】下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。
この動画を見る
下の図を、赤、青、黄、緑の4色でぬり分ける方法は何通りありますか。ただし、 使わない色があってもかまいません。
【受験算数】右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。(1) 異なる4色を用いてぬり分ける方法は何通りありますか。(2) 異なる3色を用いてぬり分ける方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。
(1) 異なる4色を用いてぬり分ける方法は何通りありますか。
(2) 異なる3色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか
この動画を見る
右の図を、赤、青、黄、緑、紫の5色でぬり分けることにします。
(1) 異なる4色を用いてぬり分ける方法は何通りありますか。
(2) 異なる3色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか
【受験算数】下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。
この動画を見る
下の図を、赤、青、黄の3色でぬり分ける方法は何通りありますか。
【数C】【空間ベクトル】四面体OABCの辺OA,OB,OCを1:1,2:1,3:1に内分する点を、P,Q,Rとする。点Cと重心Gを通る直線が平面OABと交わる点をHとする。OHをa、bを用いて表せ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCの辺OA,OB,OCをそれぞれ1:1,2:1,3:1に内分する点を、順にP,Q,Rとする。点Cと△PQRの重心Gを通る直線が平面OABと交わる点をHとする。OA=a、OB=bとするとき、OHをa、bを用いて表せ。
この動画を見る
四面体OABCの辺OA,OB,OCをそれぞれ1:1,2:1,3:1に内分する点を、順にP,Q,Rとする。点Cと△PQRの重心Gを通る直線が平面OABと交わる点をHとする。OA=a、OB=bとするとき、OHをa、bを用いて表せ。
【高校物理】光電効果の実験:図のように、光電管、直流電源、すべり抵抗器、電圧計、電流計を用いて回路をつくり、光電管の陰極P2に波長4.4✕10^(-7)mの光をあてたところ、光電流Iが流れた。次に、…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、光電管、直流電源、すべり抵抗器、電圧計、電流計を用いて回路をつくり、光電管の陰極P2に波長4.4✕10^(-7)mの光をあてたところ、光電流Iが流れた。次に、抵抗器の接点CをA側に近づけると、Iは減少し、あるところで0となった。このとき、光電管の陽極P1の電位は、陰極P2の電位よりも1.5V低かった。次の各問に答えよ。ただし、電気素量を1.6✕10^(-19)C,プランク定数を6.6✕10^(-34)J・S,真空中の光速を3.0✕10^8m/sとする。
(1) 陰極P2に照射した光の光子1個あたりのエネルギーは何Jか。
(2) 陰極P2から飛び出した電子の運動エネルギーの最大値は何Jか。
(3) 陰極P2の金属の仕事関数は何Jか。
この動画を見る
図のように、光電管、直流電源、すべり抵抗器、電圧計、電流計を用いて回路をつくり、光電管の陰極P2に波長4.4✕10^(-7)mの光をあてたところ、光電流Iが流れた。次に、抵抗器の接点CをA側に近づけると、Iは減少し、あるところで0となった。このとき、光電管の陽極P1の電位は、陰極P2の電位よりも1.5V低かった。次の各問に答えよ。ただし、電気素量を1.6✕10^(-19)C,プランク定数を6.6✕10^(-34)J・S,真空中の光速を3.0✕10^8m/sとする。
(1) 陰極P2に照射した光の光子1個あたりのエネルギーは何Jか。
(2) 陰極P2から飛び出した電子の運動エネルギーの最大値は何Jか。
(3) 陰極P2の金属の仕事関数は何Jか。
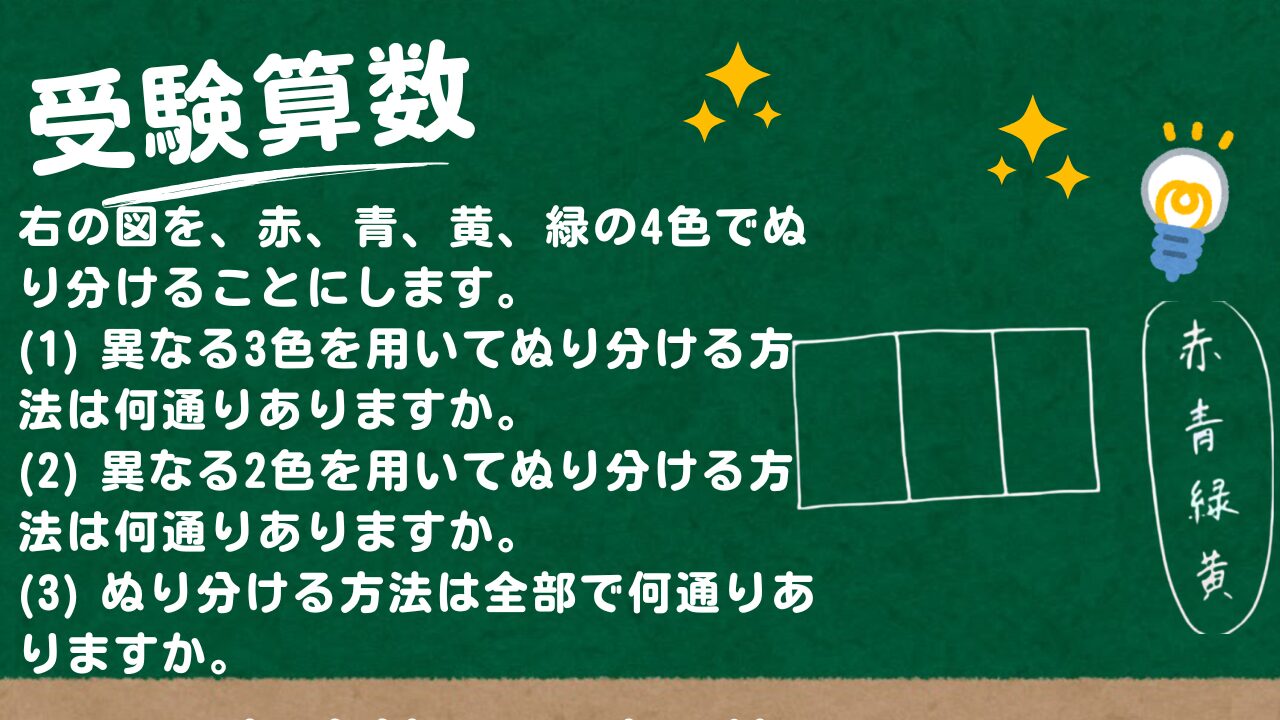
【受験算数】右の図を、赤、青、黄、緑の4色でぬり分けることにします。(1) 異なる3色を用いてぬり分ける方法は何通りありますか。(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
この動画を見る
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
【数C】【空間ベクトル】四面体OABCにおいて、△ABCの重心をG、辺OAの中点をMとし、OGと△MBCの交点をHとすると、OH:OG=3:4であることを示せ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCにおいて、△ABCの重心をG、辺OAの中点をMとし、OGと△MBCの交点をHとすると、OH:OG=3:4であることを示せ
この動画を見る
四面体OABCにおいて、△ABCの重心をG、辺OAの中点をMとし、OGと△MBCの交点をHとすると、OH:OG=3:4であることを示せ
【中学受験理科】浮力④:図の物体について次の問いに答えなさい。なお、水1cm³の重さは1gとします。問1 物体を図1のようにしたところ、ばねはかりが250gを示しました。物体は何gですか。問2 物体…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図の物体について次の問いに答えなさい。なお、水1cm³の重さは1gとします。
問1 物体を図1のようにしたところ、ばねはかりが250gを示しました。物体は何gですか。
問2 物体の中身をくりぬいて水に浮かべたところ、図2のようになりました。くりぬいた部分の体積は何cm³ ですか。
問3 問2のあと物体に水を入れたところ、図3のようになりました。入れた水の体積は何cm³ ですか。
この動画を見る
図の物体について次の問いに答えなさい。なお、水1cm³の重さは1gとします。
問1 物体を図1のようにしたところ、ばねはかりが250gを示しました。物体は何gですか。
問2 物体の中身をくりぬいて水に浮かべたところ、図2のようになりました。くりぬいた部分の体積は何cm³ ですか。
問3 問2のあと物体に水を入れたところ、図3のようになりました。入れた水の体積は何cm³ ですか。
【受験算数】下図のような道路があります。道路は右、上、右上の3方向に進むことができます。Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下図のような道路があります。道路は右、上、右上の3方向に進むことができます。
(1) PからQまで行く道順は全部で何通りありますか。
(2) Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
この動画を見る
下図のような道路があります。道路は右、上、右上の3方向に進むことができます。
(1) PからQまで行く道順は全部で何通りありますか。
(2) Aが通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
【高校物理】ミリカンの実験:図のように、極板P、Qがあり、極板間には、鉛直方向に一様な電場をかけることができる。この極板間に、帯電した油滴を漂わせ、その速度を測定することで電荷を調べる。質量m、電荷…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、極板P、Qがあり、極板間には、鉛直方向に一様な電場をかけることができる。この極板間に、帯電した油滴を漂わせ、その速度を測定することで電荷を調べる。
質量m、電荷q(>0)の油滴Aに注目すると、油滴Aが大きさvの速度で運動するとき、油滴には、速度と逆向きに大きさkvの空気抵抗がはたらく。重力加速度の大きさをgとして、次の各問に答えよ。
(1) 極板間の電場を0にしたとき、油滴Aはやがて一定の速さv1で落下した。このとき、油滴Aにはたらく力のつりあいの式を示せ。
(2) 極板間に、鉛直上向きに強さEの電場をかけたとき、油滴Aはやがて一定の速さv2で上昇した。このとき、油滴にはたらく力のつりあいの式を示せ。
(3) (1),(2)から、油滴Aの電荷qを、k,E,v1,v2を用いて表せ。
この動画を見る
図のように、極板P、Qがあり、極板間には、鉛直方向に一様な電場をかけることができる。この極板間に、帯電した油滴を漂わせ、その速度を測定することで電荷を調べる。
質量m、電荷q(>0)の油滴Aに注目すると、油滴Aが大きさvの速度で運動するとき、油滴には、速度と逆向きに大きさkvの空気抵抗がはたらく。重力加速度の大きさをgとして、次の各問に答えよ。
(1) 極板間の電場を0にしたとき、油滴Aはやがて一定の速さv1で落下した。このとき、油滴Aにはたらく力のつりあいの式を示せ。
(2) 極板間に、鉛直上向きに強さEの電場をかけたとき、油滴Aはやがて一定の速さv2で上昇した。このとき、油滴にはたらく力のつりあいの式を示せ。
(3) (1),(2)から、油滴Aの電荷qを、k,E,v1,v2を用いて表せ。
【受験算数】下図のような道路があります。PからQまで行く最短の道順を考えます。(1) 全部で何通りありますか。(2) PからAを通ってQまで行く道順は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下図のような道路があります。PからQまで行く最短の道順を考えます。
(1) 全部で何通りありますか。
(2) PからAを通ってQまで行く道順は何通りありますか。
(3) AとBの間が通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
この動画を見る
下図のような道路があります。PからQまで行く最短の道順を考えます。
(1) 全部で何通りありますか。
(2) PからAを通ってQまで行く道順は何通りありますか。
(3) AとBの間が通行止めになりました。このとき、PからQまで行く道順は何通りありますか。
【数C】【空間ベクトル】四面体OABCの辺OAの中点をM,辺BCを2:1に内分する点をQ、線分MQの中点をRとし、直線ORと平面ABCの交点をPとする。OPをa、b、cを用いて表せ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCの辺OAの中点をM,辺BCを2:1に内分する点をQ、線分MQの中点をRとし、直線ORと平面ABCの交点をPとする。OA=a、OB=b、OC=cとするとき、OPをa、b、cを用いて表せ
この動画を見る
四面体OABCの辺OAの中点をM,辺BCを2:1に内分する点をQ、線分MQの中点をRとし、直線ORと平面ABCの交点をPとする。OA=a、OB=b、OC=cとするとき、OPをa、b、cを用いて表せ
【中学受験理科】浮力③:ビーカーに水を入れ、水の浮力を確かめる実験をしました。なお、水1cm³の重さは1gとします。問1 次の物体A〜Cを図のようにして水中に入れたところ、いずれも水中で静止しました…

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ビーカーに水を入れ、水の浮力を確かめる実験をしました。なお、水1cm³の重さは1gとします。
問1 次の物体A〜Cを図のようにして水中に入れたところ、いずれも水中で静止しました。①~⑥ にあてはまる数字を答えなさい。
問2 次の物体A、Bをばねはかりでつるし、図のようにして水中に入れました。①~⑩にあてはまる数字を答えなさい。
この動画を見る
ビーカーに水を入れ、水の浮力を確かめる実験をしました。なお、水1cm³の重さは1gとします。
問1 次の物体A〜Cを図のようにして水中に入れたところ、いずれも水中で静止しました。①~⑥ にあてはまる数字を答えなさい。
問2 次の物体A、Bをばねはかりでつるし、図のようにして水中に入れました。①~⑩にあてはまる数字を答えなさい。
【受験算数】A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。
A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。
この動画を見る
A町,B町,C町の3つの町が、下図のようにいくつかの道で結ばれています。
A町からC町に行く道順は何通りありますか。ただし、同じ町を2回以上通ることはできません。
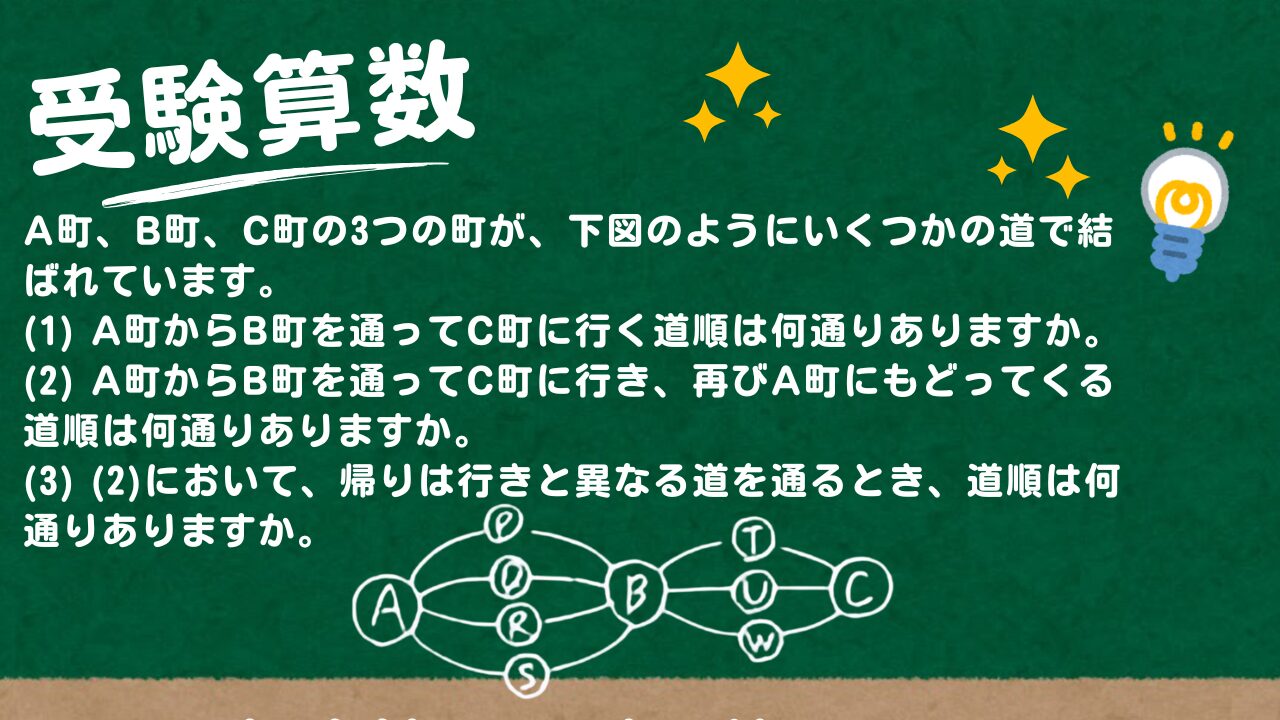
【受験算数】A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。A町からB町を通ってC町に行く道順は何通りありますか。
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。
(1) A町からB町を通ってC町に行く道順は何通りありますか。
(2) A町からB町を通ってC町に行き、再びA町にもどってくる道順は何通りありますか。
(3) (2)において、帰りは行きと異なる道を通るとき、道順は何通りありますか。
この動画を見る
A町、B町、C町の3つの町が、下図のようにいくつかの道で結ばれています。
(1) A町からB町を通ってC町に行く道順は何通りありますか。
(2) A町からB町を通ってC町に行き、再びA町にもどってくる道順は何通りありますか。
(3) (2)において、帰りは行きと異なる道を通るとき、道順は何通りありますか。
【高校物理】電気素量:ミリカンの実験において、イオンの付着によって変化する1つの油滴の電気量を観測し、次の4つの測定値が得られた。これらの測定値から、電気素量を有効数字3桁で求めよ。

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
ミリカンの実験において、イオンの付着によって変化する1つの油滴の電気量を観測し、次の4つの測定値が得られた。これらの測定値から、電気素量を有効数字3桁で求めよ。
この動画を見る
ミリカンの実験において、イオンの付着によって変化する1つの油滴の電気量を観測し、次の4つの測定値が得られた。これらの測定値から、電気素量を有効数字3桁で求めよ。
【英語】私立一貫校向け英語教材Lesson5-3 Stage3の英文解説

単元:
#英語(高校生)#英文法#接続詞
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson5
指導講師:
理数個別チャンネル
問題文全文(内容文):
I'll give you my phone number so that you can contact me anytime.
John spoke loudly so that everyone could hear him.
The traffic was so busy that I was late for the appointment.
Daniel was such a diligent boy that he learned lots of poems by heart.
He studied very hard, so that he got a perfect score on the test.
You won't get a seat unless you book one in advance.
I'll bring the mobile battery in case my phone runs out of charge.
You can use my tablet as long as you tell me beforehand.
この動画を見る
I'll give you my phone number so that you can contact me anytime.
John spoke loudly so that everyone could hear him.
The traffic was so busy that I was late for the appointment.
Daniel was such a diligent boy that he learned lots of poems by heart.
He studied very hard, so that he got a perfect score on the test.
You won't get a seat unless you book one in advance.
I'll bring the mobile battery in case my phone runs out of charge.
You can use my tablet as long as you tell me beforehand.
【受験算数】長さ260mの電車Aと長さ100mの電車Bが反対の方向に走っています。AとBの速さの比は5:4です。ある鉄橋をAとBが反対側から同時に渡り始め、同時に渡り終わりました。鉄橋の長さは何m?

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ260mの電車Aと長さ100mの電車Bが反対の方向に走っています。AとBの速さの比は5:4です。ある鉄橋を、AとBが反対側から同時にわたり始め、同時にわたり終わりました。
(1)鉄橋の長さは何mですか。
(2)AとBは、同時に鉄橋をわたり始めてから25秒後にすれちがい終わりました。Aの速さは時速何kmですか。
この動画を見る
長さ260mの電車Aと長さ100mの電車Bが反対の方向に走っています。AとBの速さの比は5:4です。ある鉄橋を、AとBが反対側から同時にわたり始め、同時にわたり終わりました。
(1)鉄橋の長さは何mですか。
(2)AとBは、同時に鉄橋をわたり始めてから25秒後にすれちがい終わりました。Aの速さは時速何kmですか。
【数B】【数列】西暦2022年1月1日に100万円を年利率7で借りた人がいる。2022年12月31日を1回とし毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#中高教材#数列
指導講師:
理数個別チャンネル
問題文全文(内容文):
西暦2022年1月1日に100万円を年利率7で借りた人がいる。この返済は、2022年12月31日を第1回とし、その後、毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ。ただし、1.07³=1.255として計算し、1円未満は切り上げよ。
この動画を見る
西暦2022年1月1日に100万円を年利率7で借りた人がいる。この返済は、2022年12月31日を第1回とし、その後、毎年年末に等額ずつ支払い、2024年年末に完済することにする。毎年年末に支払う金額を求めよ。ただし、1.07³=1.255として計算し、1円未満は切り上げよ。
【受験算数】船PがA地点からB地点まで上るのに30分、B地点からA地点まで下るのに20分かかります。船QがA地点からB地点まで上るのに40分かかります。船QがB地点からA地点まで下るのに何分かかる?

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
一定の速さで流れている川の下流にA地点、上流にB地点があります。船PがA地点からB地点まで上るのに30分、B地点からA地点まで下るのに20分かかります。また、船QがA地点からB地点まで上るのに40分かかります。船QがB地点からA地点まで下るのに何分かかりますか。ただし、船P、船Qの静水時の速さはそれぞれ一定とします。
この動画を見る
一定の速さで流れている川の下流にA地点、上流にB地点があります。船PがA地点からB地点まで上るのに30分、B地点からA地点まで下るのに20分かかります。また、船QがA地点からB地点まで上るのに40分かかります。船QがB地点からA地点まで下るのに何分かかりますか。ただし、船P、船Qの静水時の速さはそれぞれ一定とします。




