 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
なんと1分で求められる!?一橋2020年度過去問10の10乗を2020で割ったあまりを求めます!#shorts #一橋大学 #過去問

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
10の10乗を2020で割ったあまりをも求めよ
この動画を見る
10の10乗を2020で割ったあまりをも求めよ
【高校数学】毎日積分33日目【難易度:★★★★★】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
この動画を見る
次の等式が$1\leqq x\leqq 2$で成り立つような関数f(x)と定数A,Bを求めよ.
$\int_{\frac{1}{x}}^{\frac{2}{x}}|logy|f(xy)dy=3x(logx-1)+A+\frac{B}{x}$
ただし,f(x)は$1\leqq x\leqq 2$に対して定義される連続関数とする.(東京工業大学 2019)
東京海洋大学2021年度整数問題(2)解説 #shorts #過去問解説 #東京海洋大 #数学

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(2)$p$が5以上の素数であるとき、$p^2-1$は6の倍数であることを示せ
この動画を見る
(2)$p$が5以上の素数であるとき、$p^2-1$は6の倍数であることを示せ
【高校物理】毎日原子10日目【共通テストまで毎日19時投稿】
単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
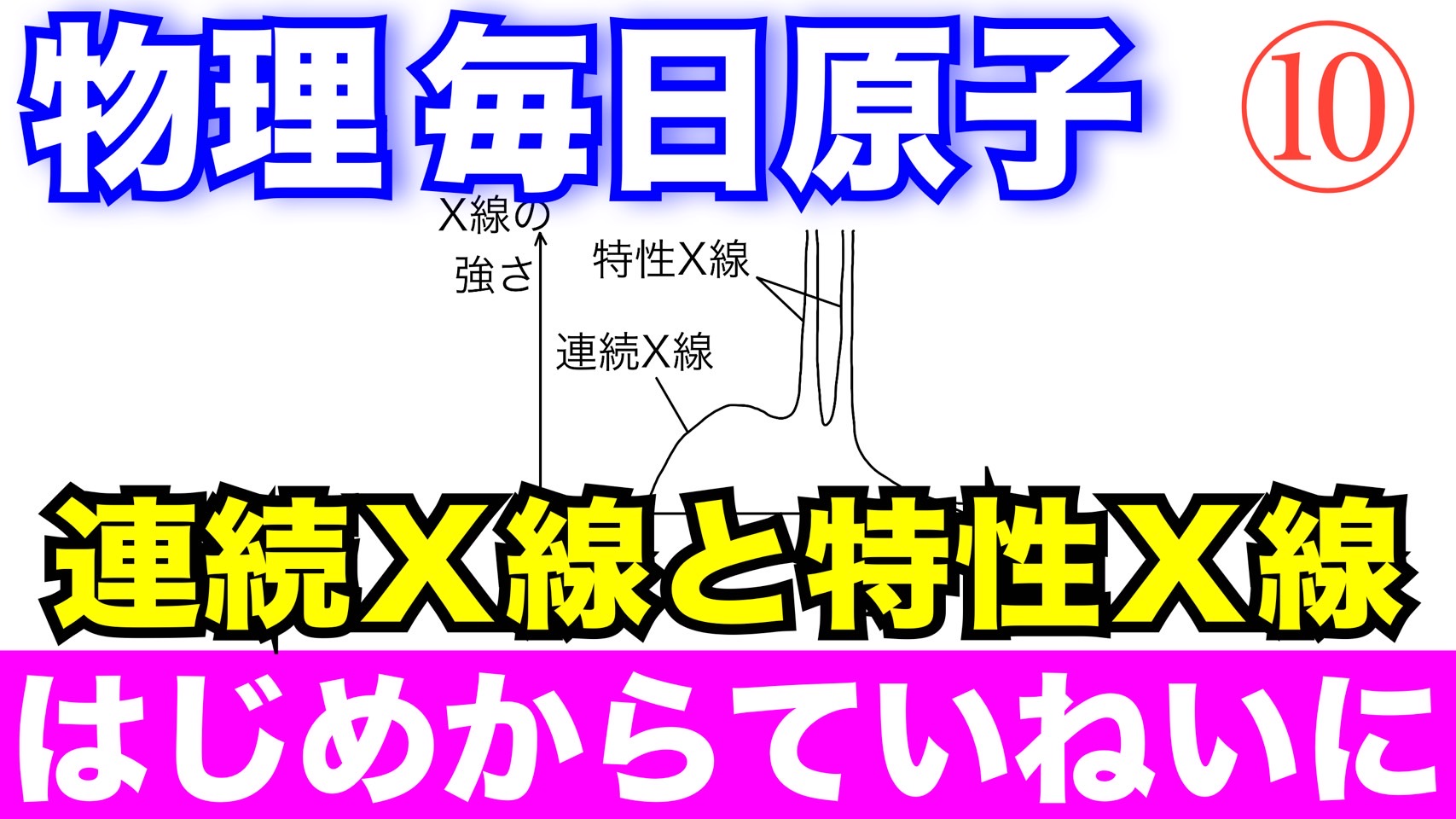
X線管において、初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を$1.6×10^{-19}$[C]、プランク定数を$6.6×10^{-34}$[J・s]、真空中の光速を$3.0×10^8$[m/s]とする。次の各問に答えよ。
(1) 加速された電子のもつエネルギーは何eVか。
(2) 連続X線の最短波長はいくらか。
(3) 加速電圧を3倍にしたとき、次の値は何倍になるか。
① 連続X線の最短波長 ② 特性X線の波長
宿題
右図は、X線管によって発生したX線のスペクトルである。プランク定数をh、光速をcとする。
(1) 右図の①、②に適当な語句を入れよ。
(2) 初速度0で陰極を出た電子(電気量−e)を電圧Vで加速し、陰極に当てたとき、陰極から放出されるX線光子の持つ最大エネルギーを求めよ。
(3)(2)のとき、X線の最短波長λ₀はいくらか。
(4) ②X線の波長をλ₁、λ₂とすると、加速電圧Vを大きくしても変化しないのは、λ₀、λ₁、λ₂ のどれか。
この動画を見る
X線管において、初速度0の電子を電圧1.5kVで加速し、陽極金属に衝突させると、X線が発生して、図のようなスペクトルが得られた。電気素量を$1.6×10^{-19}$[C]、プランク定数を$6.6×10^{-34}$[J・s]、真空中の光速を$3.0×10^8$[m/s]とする。次の各問に答えよ。
(1) 加速された電子のもつエネルギーは何eVか。
(2) 連続X線の最短波長はいくらか。
(3) 加速電圧を3倍にしたとき、次の値は何倍になるか。
① 連続X線の最短波長 ② 特性X線の波長
宿題
右図は、X線管によって発生したX線のスペクトルである。プランク定数をh、光速をcとする。
(1) 右図の①、②に適当な語句を入れよ。
(2) 初速度0で陰極を出た電子(電気量−e)を電圧Vで加速し、陰極に当てたとき、陰極から放出されるX線光子の持つ最大エネルギーを求めよ。
(3)(2)のとき、X線の最短波長λ₀はいくらか。
(4) ②X線の波長をλ₁、λ₂とすると、加速電圧Vを大きくしても変化しないのは、λ₀、λ₁、λ₂ のどれか。
【高校数学】毎日積分32日目【共通テスト直前特別編】【毎日17時投稿】

英検準2級ライティング全パターン紹介 #shorts #英検準2級 #ライティング
単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検準2級ライティング全パターン紹介していきます.
この動画を見る
英検準2級ライティング全パターン紹介していきます.
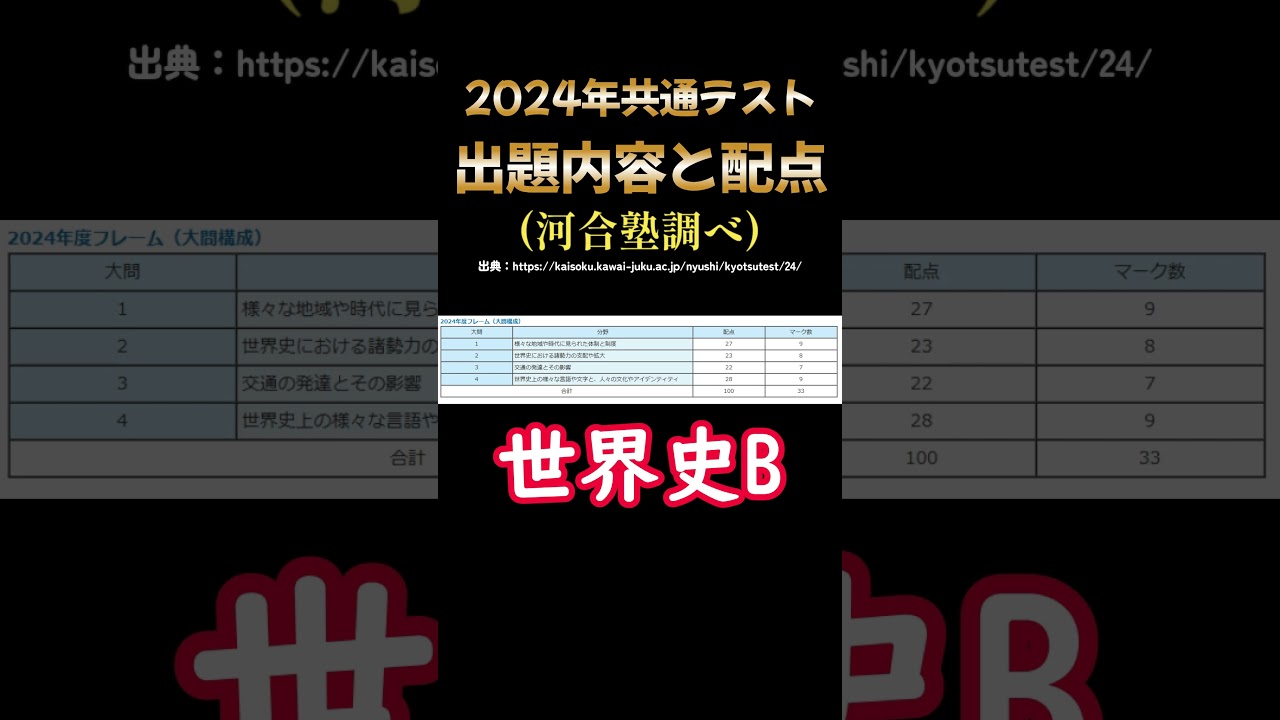
2024年共通テスト社会の出題範囲と配点速報 #shorts #共通テスト #世界史 #日本史 #地理 #倫理政経
単元:
#社会(高校生)#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#大学入試解答速報#世界史#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
2024年共通テスト社会の出題範囲と配点速報
この動画を見る
2024年共通テスト社会の出題範囲と配点速報
【高校物理】毎日原子9日目【共通テストまで毎日19時投稿】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
定常状態の水素原子では、質量m、電気量-eの電子が、電気量+eの原子核(陽子)の周りを、半径r、速さvで等速円運動していると考えられる。クーロンの法則の比例定数をkとすると、円運動の式は(1)となる。また、電子は粒子であると同時に、波の性質ももっていて、プランク定数を h とすると、その波長λはλ=(2)となる。この波動性に対して、ボーアは(3)の条件を満たしていると考えた。ただし、nは自然数とする。以上の関係式からrとnの関係に注目すると、rは(4)に比例し、軌道半径はnによって定まる不連続な値しかとり得ないことがわかった。
この動画を見る
定常状態の水素原子では、質量m、電気量-eの電子が、電気量+eの原子核(陽子)の周りを、半径r、速さvで等速円運動していると考えられる。クーロンの法則の比例定数をkとすると、円運動の式は(1)となる。また、電子は粒子であると同時に、波の性質ももっていて、プランク定数を h とすると、その波長λはλ=(2)となる。この波動性に対して、ボーアは(3)の条件を満たしていると考えた。ただし、nは自然数とする。以上の関係式からrとnの関係に注目すると、rは(4)に比例し、軌道半径はnによって定まる不連続な値しかとり得ないことがわかった。
【高校数学】毎日積分31日目【共通テスト直前特別編】【毎日17時投稿】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テストでも使える!?面積を求めるときの積分の公式についてまとめました!
この動画を見る
共通テストでも使える!?面積を求めるときの積分の公式についてまとめました!
【高校物理】毎日原子5日目「放射線の進路」の宿題を解いてみた【番外編】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように,真空中に放射線源と磁石を配置した。α線,β線,γ線の放射線が放射線源から鉛直上向きに飛び出したとすると,各々の放射線の進路はどのようになるか,図の(a)~(c)から選べ。
この動画を見る
図のように,真空中に放射線源と磁石を配置した。α線,β線,γ線の放射線が放射線源から鉛直上向きに飛び出したとすると,各々の放射線の進路はどのようになるか,図の(a)~(c)から選べ。
今までありがとうございました!最後の動画となります。【55日目】毎日3分古文単語【325~330】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
325.よのつねなり(2)
326.ただならず(3)
327.ものもおぼえず(2)
328.ひとやりならず(1)
329.またのひ(1)
330.~あへず(1)
この動画を見る
325.よのつねなり(2)
326.ただならず(3)
327.ものもおぼえず(2)
328.ひとやりならず(1)
329.またのひ(1)
330.~あへず(1)
【共通テストでも使える!?】面積を求める1/ 6公式をメチャクチャ分かりやすく解説!例題もあるよ!

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1/6公式を超絶分かりやすく解説!さらに例題も演習!
次の放物線とx軸で囲まれた図形の面積Sを求めよ。
$y=-x^2+2x+3$
この動画を見る
1/6公式を超絶分かりやすく解説!さらに例題も演習!
次の放物線とx軸で囲まれた図形の面積Sを求めよ。
$y=-x^2+2x+3$
【高校物理】毎日原子8日目【共通テストまで毎日19時投稿】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように格子面の間隔(格子定数)が$d$で、原子が規則的に配列している結晶に、波長$λ$の特性$X$線が格子面に対して角$\theta$で入射している。
(1) 格子面1、格子面2で反射した2つのX線の経路差を$d、\theta$を用いて表せ。
(2) 反射$X$線の強めあう条件を、$d、\theta、λ$、正の数$n(=1、2、…)$を用いて表せ。
(3) $θ$を0°から大きくしていくと、$\theta=\theta_0$のとき、はじめて反射$X$線が強めあった。格子定数$d$を、$\theta_0、λ$を用いて表せ。
この動画を見る
図のように格子面の間隔(格子定数)が$d$で、原子が規則的に配列している結晶に、波長$λ$の特性$X$線が格子面に対して角$\theta$で入射している。
(1) 格子面1、格子面2で反射した2つのX線の経路差を$d、\theta$を用いて表せ。
(2) 反射$X$線の強めあう条件を、$d、\theta、λ$、正の数$n(=1、2、…)$を用いて表せ。
(3) $θ$を0°から大きくしていくと、$\theta=\theta_0$のとき、はじめて反射$X$線が強めあった。格子定数$d$を、$\theta_0、λ$を用いて表せ。
【高校数学】毎日積分30日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
この動画を見る
$\int_0^1\sqrt{1+2\sqrt{x}}dx$
これを解け.
絵や写真で覚える「毎日3分古文単語54日目」 #古文単語 #毎日3分古文単語 #shorts

【高校物理】毎日原子6日目「光電効果」の宿題を解いてみた【番外編】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s],プランク定数をh=$6.6×10^{-34}$[J・s],電気素量を$1.6×10^{-19}$[C]とする。この光の光子1個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。
この動画を見る
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s],プランク定数をh=$6.6×10^{-34}$[J・s],電気素量を$1.6×10^{-19}$[C]とする。この光の光子1個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。
【高校物理】毎日原子3日目「半減期」の宿題を解いてみた【番外編】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
古代遺跡から発掘された植物体内の$^{14}C$ の$^{12}C$ に対する割合は,大気中のそれの0.71倍であった。この発掘された植物は今からおよそ何年前に生育していたものと推定されるか。これを有効数字2桁で表すとき,次の式中の空欄ア〜ウに入れる数字として最も適当なものを答えよ。ただし,$^{14}C$ のβ崩壊の半減期は$5.73×10^3$年であり,大気中の$^{14}C$ と$^{12}C$ の割合は常に一定とする。また,$\frac{1}{\sqrt{2}}=0.71$である。$ □ .□×10^□$
この動画を見る
古代遺跡から発掘された植物体内の$^{14}C$ の$^{12}C$ に対する割合は,大気中のそれの0.71倍であった。この発掘された植物は今からおよそ何年前に生育していたものと推定されるか。これを有効数字2桁で表すとき,次の式中の空欄ア〜ウに入れる数字として最も適当なものを答えよ。ただし,$^{14}C$ のβ崩壊の半減期は$5.73×10^3$年であり,大気中の$^{14}C$ と$^{12}C$ の割合は常に一定とする。また,$\frac{1}{\sqrt{2}}=0.71$である。$ □ .□×10^□$
【54日目】毎日3分古文単語【319~324】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
319.させる(連体詞)(1)
320.さはれ(感動詞)(1)
321.いとしもなし(1)
322.かずならず(1)
323.いかにぞや(1)
324.さればよ・さればこそ(1)
この動画を見る
<今日の単語>
319.させる(連体詞)(1)
320.さはれ(感動詞)(1)
321.いとしもなし(1)
322.かずならず(1)
323.いかにぞや(1)
324.さればよ・さればこそ(1)
英検2級ライティング問題のテンプレ当てはめ例【2分でコメント返信/AI採点で満点】概要欄にテンプレ元の動画URL(サムネ画像はテンプレ元動画)

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検2級ライティング問題のテンプレ当てはめ例に関して解説していきます.
この動画を見る
英検2級ライティング問題のテンプレ当てはめ例に関して解説していきます.
【英語】Lesson10-2 Stage3【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#中2英語#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson10-2 Stage3解説していきます.
この動画を見る
Lesson10-2 Stage3解説していきます.
英検準1級2023年3回予想問題5選【先着100件は添削します】#英検準1級 #ライティング #shorts

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
予想問題①
TOPIC
Should cities invest more in creating green spaces like parks and gardens?
POINTS
・Mental health benefits
・Maintenance costs
・Urban development
・Environmental impact
予想問題②
TOPIC
Agree or disagree: Schools should incorporate more virtual reality (VR) technologies in education.
POINTS
・Educational effectiveness
・Technology costs
・Student engagement
・Technological access and equality
予想問題③
TOPIC
Should the use of electric scooters be promoted as a primary mode of transportation in urban areas?
POINTS
・Traffic congestion
・Safety concerns
・Environmental benefits
・Infrastructure requirements
予想問題④
TOPIC
Agree or disagree: Employers should offer more flexible working hours to improve work-life balance.
POINTS
・Employee productivity
・Workforce management
・Employee well-being
・Impact on business operations
予想問題⑤
TOPIC
Should governments prioritize funding for renewable energy research over fossil fuels?
POINTS
・Long-term environmental impact
・Economic feasibility
・Energy security
・Job creation in the energy sector
この動画を見る
予想問題①
TOPIC
Should cities invest more in creating green spaces like parks and gardens?
POINTS
・Mental health benefits
・Maintenance costs
・Urban development
・Environmental impact
予想問題②
TOPIC
Agree or disagree: Schools should incorporate more virtual reality (VR) technologies in education.
POINTS
・Educational effectiveness
・Technology costs
・Student engagement
・Technological access and equality
予想問題③
TOPIC
Should the use of electric scooters be promoted as a primary mode of transportation in urban areas?
POINTS
・Traffic congestion
・Safety concerns
・Environmental benefits
・Infrastructure requirements
予想問題④
TOPIC
Agree or disagree: Employers should offer more flexible working hours to improve work-life balance.
POINTS
・Employee productivity
・Workforce management
・Employee well-being
・Impact on business operations
予想問題⑤
TOPIC
Should governments prioritize funding for renewable energy research over fossil fuels?
POINTS
・Long-term environmental impact
・Economic feasibility
・Energy security
・Job creation in the energy sector
英検2級2023年3回予想問題5選【先着100件は添削します】#英検2級 #ライティング #shorts

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
2023年3回予想問題
予想問題①
TOPIC: With the rise in remote work, some suggest that companies should provide financial support for home office setups. Do you agree with this opinion?
POINTS: Productivity, Equity, Cost
予想問題②
TOPIC: As electric vehicles become more popular, some believe that all gas stations should offer electric charging stations. Do you think this is a necessary step?
POINTS: Environmental impact, Infrastructure costs, Accessibility
予想問題③
TOPIC: There is a growing trend of using artificial intelligence in educational settings, such as for grading or personalized learning plans. Do you believe this trend will continue to grow?
POINTS: Educational quality, Technology dependence, Privacy concerns
予想問題④
TOPIC: Some cities are considering making public transportation free to reduce traffic and pollution. Do you support this initiative?
POINTS: Environmental benefits, Government budget, Public convenience
予想問題⑤
TOPIC: With advancements in technology, there's a possibility of having a four-day workweek. Do you think this will become a common practice in the future?
POINTS: Work-life balance, Productivity, Economic impact
この動画を見る
2023年3回予想問題
予想問題①
TOPIC: With the rise in remote work, some suggest that companies should provide financial support for home office setups. Do you agree with this opinion?
POINTS: Productivity, Equity, Cost
予想問題②
TOPIC: As electric vehicles become more popular, some believe that all gas stations should offer electric charging stations. Do you think this is a necessary step?
POINTS: Environmental impact, Infrastructure costs, Accessibility
予想問題③
TOPIC: There is a growing trend of using artificial intelligence in educational settings, such as for grading or personalized learning plans. Do you believe this trend will continue to grow?
POINTS: Educational quality, Technology dependence, Privacy concerns
予想問題④
TOPIC: Some cities are considering making public transportation free to reduce traffic and pollution. Do you support this initiative?
POINTS: Environmental benefits, Government budget, Public convenience
予想問題⑤
TOPIC: With advancements in technology, there's a possibility of having a four-day workweek. Do you think this will become a common practice in the future?
POINTS: Work-life balance, Productivity, Economic impact
【高校物理】毎日原子7日目【共通テストまで毎日19時投稿】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、波長λ[m]のX線を質量m[kg]の静止している電子に向けて入射したとき、電子は図のθの方向に速さv〔m/s)でたたき出され、入射線はθ’の方向に波長でλ’[m]となって散乱されたとする。プランク定数をh[J・s]、光速をc[m/s]とする。
(1) X線の入射方向の運動量保存則を表せ。
(2) X線の入射方向に垂直な方向の運動量保存則を表せ。
(3) 衝突前後のエネルギー保存の法則を表せ。
宿題
真空中に静止していた質量 m[kg]の電子に波長λ[m]のX線光子を衝突させる。
電子はX線の入射方向 θ の角をなす方向に速さ v[m/s]ではね飛ばされ、X線光子は
入射方向と垂直な方向に波長λ’[m]となって散乱された。光速をc[m/s]、プラ
ンク定数をh[J・s]とする。
(1)衝突前後のエネルギー保存則を表せ。
(2)X線の入射方向に関する運動量保存則を表せ。
(3)X線の入射方向に垂直な方向に関する運動量保存則を表せ。
この動画を見る
図のように、波長λ[m]のX線を質量m[kg]の静止している電子に向けて入射したとき、電子は図のθの方向に速さv〔m/s)でたたき出され、入射線はθ’の方向に波長でλ’[m]となって散乱されたとする。プランク定数をh[J・s]、光速をc[m/s]とする。
(1) X線の入射方向の運動量保存則を表せ。
(2) X線の入射方向に垂直な方向の運動量保存則を表せ。
(3) 衝突前後のエネルギー保存の法則を表せ。
宿題
真空中に静止していた質量 m[kg]の電子に波長λ[m]のX線光子を衝突させる。
電子はX線の入射方向 θ の角をなす方向に速さ v[m/s]ではね飛ばされ、X線光子は
入射方向と垂直な方向に波長λ’[m]となって散乱された。光速をc[m/s]、プラ
ンク定数をh[J・s]とする。
(1)衝突前後のエネルギー保存則を表せ。
(2)X線の入射方向に関する運動量保存則を表せ。
(3)X線の入射方向に垂直な方向に関する運動量保存則を表せ。
【高校数学】毎日積分29日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.
この動画を見る
$\int_1^4\frac{dx}{\sqrt{3-\sqrt{x}}}$
これを解け.
中国王朝の覚え歌(カラオケ)#世界史 #中国史 #shorts

単元:
#社会(高校生)#世界史#アジア・アメリカの古代文明#内陸アジア世界・東アジア世界の形成#内陸アジア世界・東アジア世界の展開#アジア諸地域の繁栄#アジア諸地域の動揺#帝国主義とアジアの民族運動#二つの世界大戦#冷戦と第三世界の独立
指導講師:
理数個別チャンネル
問題文全文(内容文):
※周(東周)のなかに春秋戦国時代があったり、漢には前漢→新→後漢という移り変わりがあったりしますが、最初は主要な王朝を覚えることが大事なので、まずはこの歌で覚えましょう。
この動画を見る
※周(東周)のなかに春秋戦国時代があったり、漢には前漢→新→後漢という移り変わりがあったりしますが、最初は主要な王朝を覚えることが大事なので、まずはこの歌で覚えましょう。
【53日目】毎日3分古文単語【313~318】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
313.つくづくと(1)
314.せめて(2)
315.さりとも(1)
316.さて(2)
317.おほかた~打消(1)
318.かまへて(3)
この動画を見る
<今日の単語>
313.つくづくと(1)
314.せめて(2)
315.さりとも(1)
316.さて(2)
317.おほかた~打消(1)
318.かまへて(3)
【英語】Lesson10-1 Stage3【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#中2英語#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage3 Lesson10-1のkey pointを解説したものになります。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage3 Lesson10-1のkey pointを解説したものになります。
Lesson10-1 NT Stage3 3rd Edition【ぐっさんの英語部屋がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#比較#比較(比較級、最上級、more,mostを使った比較、as~asの文、不規則変化するもの、疑問詞で始まる比較の文)
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson10
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage3 Lesson10-1のkey pointを解説したものになります。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage3 Lesson10-1のkey pointを解説したものになります。
【高校物理】毎日原子6日目【共通テストまで毎日19時投稿】

単元:
#物理#理科(高校生)#原子
指導講師:
理数個別チャンネル
問題文全文(内容文):
仕事関数が2.0[eV]の金属の表面に波長$4.0×10^{-7}$[m]の光を当てた。プランク定数をh=$6.6×10^{-34}$[J・s]、真空中の光の速さをc=$3.0×10^8$[m/s]、電気素量を$1.6×10^{-19}$[C]とする。金属の表面から飛び出してくる電子の運動エネルギーの最大値は□.□[eV]である。
宿題
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s],プランク定数をh=$6.6×10^{-34}$[J・s],電気素量を$1.6×10^{-19}$[C]とする。この光の光子1個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。
この動画を見る
仕事関数が2.0[eV]の金属の表面に波長$4.0×10^{-7}$[m]の光を当てた。プランク定数をh=$6.6×10^{-34}$[J・s]、真空中の光の速さをc=$3.0×10^8$[m/s]、電気素量を$1.6×10^{-19}$[C]とする。金属の表面から飛び出してくる電子の運動エネルギーの最大値は□.□[eV]である。
宿題
仕事関数が1.8[eV]の金属の表面に真空中での波長が$4.0×10^{-7}$[m]の光を当てる。真空中の光の速さをc=$3.0×10^8$[m/s],プランク定数をh=$6.6×10^{-34}$[J・s],電気素量を$1.6×10^{-19}$[C]とする。この光の光子1個のエネルギーは□.□[eV]である。金属の表面から飛び出した光電子の最大の運動エネルギーは□.□[eV]である。
【高校数学】毎日積分28日目【難易度:★★★】【毎日17時投稿】





