 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数学】中高一貫校問題集2幾何133:円:接弦定理: 相似の証明2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
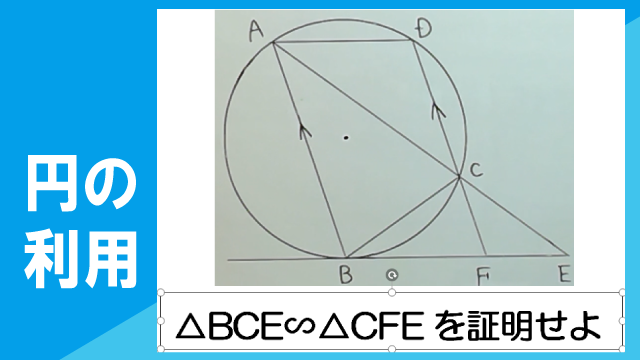
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
この動画を見る
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
【数学】中高一貫校問題集2幾何132:円:接弦定理: 相似の証明1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
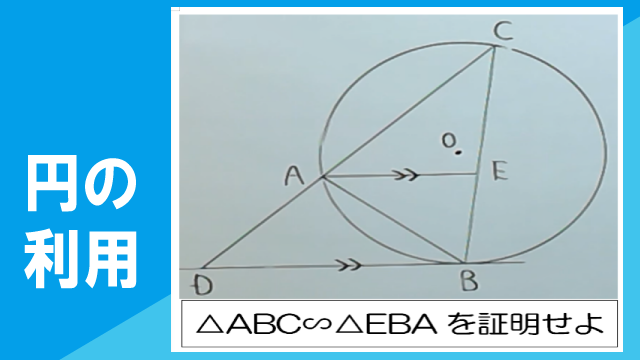
右の図において、△ABCは円Oに内接し、辺BCは辺ABよりも長い。点Bにおける円Oの接線と辺CAの延長との交点をDとし、辺BC上に点Eを、AE//DBとなるようにとる。このとき△ABC∽△EBAであることを証明しなさい。
この動画を見る
右の図において、△ABCは円Oに内接し、辺BCは辺ABよりも長い。点Bにおける円Oの接線と辺CAの延長との交点をDとし、辺BC上に点Eを、AE//DBとなるようにとる。このとき△ABC∽△EBAであることを証明しなさい。
【数学】中高一貫校問題集2幾何131:円:接弦定理:二等辺三角形の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
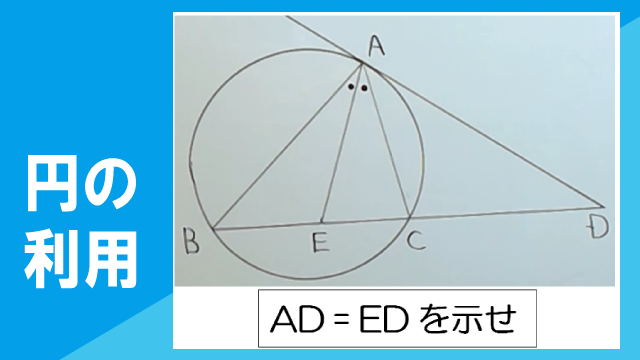
右の図のように、△ABCとその外接円があり、点Aにおける外接円の接線が辺BCの延長と交わる点をDとする。また、∠BACの二等分線がBCと交わる点をEとする。このとき、AD=EDであることを証明しなさい。
この動画を見る
右の図のように、△ABCとその外接円があり、点Aにおける外接円の接線が辺BCの延長と交わる点をDとする。また、∠BACの二等分線がBCと交わる点をEとする。このとき、AD=EDであることを証明しなさい。
Lesson12-1 ニュートレジャー Stage3 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(高校生)#英文法#分詞・分詞構文
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson12-1 『強調』についての解説動画です。
入試最頻出の構文『強調構文』についても詳しく解説しています。形式主語構文との違いについても触れています。
この動画を見る
Lesson12-1 『強調』についての解説動画です。
入試最頻出の構文『強調構文』についても詳しく解説しています。形式主語構文との違いについても触れています。
Lesson11-2 NT Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(高校生)#英文法#仮定法
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson11
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson11-2(仮定法の表現)の解説動画です。
仮定法のさまざまな表現を解説しています。「~がなければ」の言い換え、timeの前のhighが何であるかなどの小ネタも。
例文
I feel sick today. I wish I had taken some medicine last night.
Ron looked really scared. He looked as if he had seen a ghost.
If it were not for the smartphone, I wouldn't be able to meet you on time.
It's high time you made up with Tom.
If only I had more time to discuss the topic.
If it should rain, we wouldn't arrive at the station in time.
If the sun were to disappear, we wouldn't be able to live a day.
この動画を見る
N.T. Lesson11-2(仮定法の表現)の解説動画です。
仮定法のさまざまな表現を解説しています。「~がなければ」の言い換え、timeの前のhighが何であるかなどの小ネタも。
例文
I feel sick today. I wish I had taken some medicine last night.
Ron looked really scared. He looked as if he had seen a ghost.
If it were not for the smartphone, I wouldn't be able to meet you on time.
It's high time you made up with Tom.
If only I had more time to discuss the topic.
If it should rain, we wouldn't arrive at the station in time.
If the sun were to disappear, we wouldn't be able to live a day.
Lesson11-2 ニュートレジャー Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(高校生)#英文法#仮定法
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson11-2(仮定法の表現)の解説動画です。
仮定法のさまざまな表現を解説しています。「~がなければ」の言い換え、timeの前のhighが何であるかなどの小ネタも。
この動画を見る
N.T. Lesson11-2(仮定法の表現)の解説動画です。
仮定法のさまざまな表現を解説しています。「~がなければ」の言い換え、timeの前のhighが何であるかなどの小ネタも。
Lesson11-1 NT Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(高校生)#英文法#仮定法
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson11
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage3 Lesson11-1で扱われている仮定法過去完了について解説しています。
If I had had time, I would accepted your offer.
If I had been brought up in the US, I would be able to speak English better now.
If I were you, I would have refused to help him.
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage3 Lesson11-1で扱われている仮定法過去完了について解説しています。
If I had had time, I would accepted your offer.
If I had been brought up in the US, I would be able to speak English better now.
If I were you, I would have refused to help him.
Lesson11-1 ニュートレジャー Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(高校生)#英文法#仮定法
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage3 Lesson11-1で扱われている仮定法過去完了について解説しています。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage3 Lesson11-1で扱われている仮定法過去完了について解説しています。
Lesson9-1 NT Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(高校生)#英文法#分詞・分詞構文#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson9
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson9-1の解説動画です。
補語になる分詞の特徴を解説します。2018年の明治大学の商学部の入試問題にも触れています。
例文
After the class was over, we all sat talking for an hour.
Mr. White stood surrounded by his students.
Jason did his best to work Lucy ( ) the seriousness of the problem.(明治大・商学部 2018)
この動画を見る
N.T. Lesson9-1の解説動画です。
補語になる分詞の特徴を解説します。2018年の明治大学の商学部の入試問題にも触れています。
例文
After the class was over, we all sat talking for an hour.
Mr. White stood surrounded by his students.
Jason did his best to work Lucy ( ) the seriousness of the problem.(明治大・商学部 2018)
Lesson9-1 ニュートレジャー Stage3 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#動名詞(動詞の目的語、主語・補語・前置詞の目的語、動名詞と不定詞)
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. Lesson9-1の解説動画です。
補語になる分詞の特徴を解説します。2018年の明治大学の商学部の入試問題にも触れています。
この動画を見る
N.T. Lesson9-1の解説動画です。
補語になる分詞の特徴を解説します。2018年の明治大学の商学部の入試問題にも触れています。
Lesson2-2 NT Stage3 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#助動詞#can、could、be able to、may、must、have to、should、助動詞を使った表現
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson2
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage3 Lesson2-2 の解説動画です。
can /couldの推量で使われる意味、またcould / was(were)able to の「できた」の違い
will / would の「習慣・意思・性質」の意味、would / used to の違いについても解説します。
Practicing musical instruments can be hard for everyone.
Mike cannot be good at playing the drums. He only started practicing them last week.
One day he could be famous, but the chances are very small.
He could play the guitar when he was on elementary school student.
He was able to find Mary's house easily.
Children will behave like children.
The window won't open.
My brother would often play the trumpet in this room.
I used to like American pop music, but now I prefer K-pop.
There used to be a furniture shop over there, but now it's closed down.
この動画を見る
N.T. SERIES Third Edition Stage3 Lesson2-2 の解説動画です。
can /couldの推量で使われる意味、またcould / was(were)able to の「できた」の違い
will / would の「習慣・意思・性質」の意味、would / used to の違いについても解説します。
Practicing musical instruments can be hard for everyone.
Mike cannot be good at playing the drums. He only started practicing them last week.
One day he could be famous, but the chances are very small.
He could play the guitar when he was on elementary school student.
He was able to find Mary's house easily.
Children will behave like children.
The window won't open.
My brother would often play the trumpet in this room.
I used to like American pop music, but now I prefer K-pop.
There used to be a furniture shop over there, but now it's closed down.
Lesson2-2 ニュートレジャー Stage3 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中3英語#未来の文・助動詞(will,be going to,can,could,may,might,must,have to,should,shall,would,had better,used to,ought to)
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage3 Lesson2-2 の解説動画です。
can /couldの推量で使われる意味、またcould / was(were)able to の「できた」の違い
will / would の「習慣・意思・性質」の意味、would / used to の違いについても解説します。
この動画を見る
N.T. SERIES Third Edition Stage3 Lesson2-2 の解説動画です。
can /couldの推量で使われる意味、またcould / was(were)able to の「できた」の違い
will / would の「習慣・意思・性質」の意味、would / used to の違いについても解説します。
Lesson2-1 NT Stage3 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中2英語#助動詞#can、could、be able to、may、must、have to、should、助動詞を使った表現
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson2
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage3 Lesson2-1の解説動画です。
助動詞は暗記がメインであることを踏まえ、暗記が少しでもラクになるための勉強法や法則、分類の仕方を指導しています。
今回はメインの助動詞のうち、推量の意味を中心に指導してmustの周辺や、not の位置などテストに出題されたら間違えやすいものを強調して例文の解説を行っています。
If it's stormy, the train may stop running.
The typhoon might be stronger than I expected.
Your parents have been waiting for your call. They must be anxious.
The ship should leave around lunch time.
You ought to check the exact time of departure.
※She had better wear her sunglasses because the sun is strong today.
※Traffic may be heavy on Friday evening, so they had better not take the bus.
この動画を見る
N.T. SERIES Third Edition Stage3 Lesson2-1の解説動画です。
助動詞は暗記がメインであることを踏まえ、暗記が少しでもラクになるための勉強法や法則、分類の仕方を指導しています。
今回はメインの助動詞のうち、推量の意味を中心に指導してmustの周辺や、not の位置などテストに出題されたら間違えやすいものを強調して例文の解説を行っています。
If it's stormy, the train may stop running.
The typhoon might be stronger than I expected.
Your parents have been waiting for your call. They must be anxious.
The ship should leave around lunch time.
You ought to check the exact time of departure.
※She had better wear her sunglasses because the sun is strong today.
※Traffic may be heavy on Friday evening, so they had better not take the bus.
【中学受験社会】江戸時代の将軍の年号の覚え方

Lesson2-1 ニュートレジャー Stage3 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中2英語#can、could、be able to、may、must、have to、should、助動詞を使った表現#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回はメインの助動詞のうち、推量の意味を中心に指導してmustの周辺や、not の位置などテストに出題されたら間違えやすいものを強調して例文の解説を行っています。
この動画を見る
今回はメインの助動詞のうち、推量の意味を中心に指導してmustの周辺や、not の位置などテストに出題されたら間違えやすいものを強調して例文の解説を行っています。
【7日目】毎日3分古文単語【37~42】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
37.ほど(4)
38.なさけ(3)
39.ちぎり(3)
40.けしき(3)
41.いと(2)
42.あまた(1)
この動画を見る
<今日の単語>
37.ほど(4)
38.なさけ(3)
39.ちぎり(3)
40.けしき(3)
41.いと(2)
42.あまた(1)
【数学】中高一貫校問題集2幾何130:円:接弦定理
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
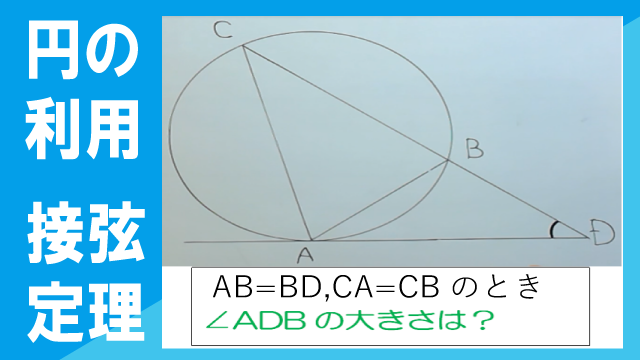
右の図において、ADは円の接線で、AB=BD、CA=CBである。このとき、∠ADBの大きさを求めなさい。
この動画を見る
右の図において、ADは円の接線で、AB=BD、CA=CBである。このとき、∠ADBの大きさを求めなさい。
【日本最速解答速報】2024年明治薬科大学薬学部薬学科(6年制)公募制推薦 英語解答速報 2023年11月18日(土)実施【YAKISOBA先生】

単元:
#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#大学入試解答速報#英語#明治薬科大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2023年11月18日(土)に実施された、2024年明治薬科大学薬学部薬学科(6年制)公募制推薦の英語解答速報です。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院センター南校のYAKISOBA先生です。
試験に出ている文章は辞書の例文そのままを使っている・・・?
この動画を見る
こちらの動画は、2023年11月18日(土)に実施された、2024年明治薬科大学薬学部薬学科(6年制)公募制推薦の英語解答速報です。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院センター南校のYAKISOBA先生です。
試験に出ている文章は辞書の例文そのままを使っている・・・?
【日本最速解答速報】2024年明治薬科大学薬学部薬学科(6年制)公募制推薦 英語解答速報【YAKISOBA先生】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
この動画を見る
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
【6日目】毎日3分古文単語【31~36】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
31.としごろ(1)
32.かたち(1)
33.かげ(2)
34.ほい(1)
35.ものがたり(2)
36.ふみ(2)
この動画を見る
<今日の単語>
31.としごろ(1)
32.かたち(1)
33.かげ(2)
34.ほい(1)
35.ものがたり(2)
36.ふみ(2)
【日本最速解答速報】2024年明治薬科大学薬学部薬学科(6年制)公募制推薦 数学解答速報 2023年11月18日(土)実施【TAKAHASHI名人】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報#数学#明治薬科大学
指導講師:
理数個別チャンネル
問題文全文(内容文):
こちらの動画は、2023年11月18日(土)に実施された、2024年明治薬科大学薬学部薬学科(6年制)公募制推薦の数学解答速報です。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院センター南校のTAKAHASHI名人です。
この動画を見る
こちらの動画は、2023年11月18日(土)に実施された、2024年明治薬科大学薬学部薬学科(6年制)公募制推薦の数学解答速報です。
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
解説者は理数個別指導学院センター南校のTAKAHASHI名人です。
【日本最速解答速報】2024年明治薬科大学薬学部薬学科(6年制)公募制推薦 数学解答速報【TAKAHASHI名人】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
この動画を見る
大学の正解発表ではなく、あくまで当チャンネルの講師が独自に解説をしているものですので、万が一内容に間違いがございましたらご容赦ください。
「毎日3分古文単語」を5日間見てくれた方にプレゼントがあります!!

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
共通テスト前日まで「毎朝7時」に投稿するので、通学の電車内や寝る前などに見てください。単語暗記をルーティンにしよう!
この動画を見る
共通テスト前日まで「毎朝7時」に投稿するので、通学の電車内や寝る前などに見てください。単語暗記をルーティンにしよう!
【5日目】毎日3分古文単語【25~30】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
25.わびし(2)
26.あはれなり(1)
27.おろかなり(2)
28.ねんごろなり(2)
29.つれづれなり(2)
30.いたづらなり(2)
この動画を見る
<今日の単語>
25.わびし(2)
26.あはれなり(1)
27.おろかなり(2)
28.ねんごろなり(2)
29.つれづれなり(2)
30.いたづらなり(2)
【数学】中高一貫校問題集2幾何129:円:接弦定理:弧の比と円周角の比
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
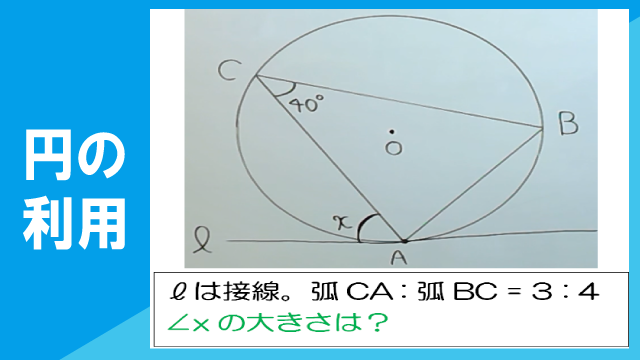
右の図において、直線?は点Aで円Oに接していて、∠ACB=40°である。また、弧AC:弧CB=3:4である。このとき、∠xの大きさを求めなさい。
この動画を見る
右の図において、直線?は点Aで円Oに接していて、∠ACB=40°である。また、弧AC:弧CB=3:4である。このとき、∠xの大きさを求めなさい。
【数学】中高一貫校問題集2幾何124:円:円の接線:外心、内心、重心はどれ?
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
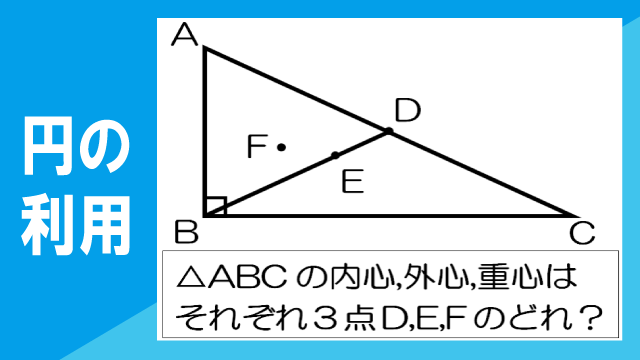
図の△ABCは、∠B=90°の直角三角形であり、3点D、E、Fは△ABCの外心、内心、重心のいずれかである。このとき、△ABCの外心、内心、重心はそれぞれ3点D、E、Fのいずれかであるか答えなさい。
この動画を見る
図の△ABCは、∠B=90°の直角三角形であり、3点D、E、Fは△ABCの外心、内心、重心のいずれかである。このとき、△ABCの外心、内心、重心はそれぞれ3点D、E、Fのいずれかであるか答えなさい。
共通テストにまだ間に合う!毎日3分古文単語暗記! #単語 #共通テスト対策 #古文単語 #shorts
【4日目】毎日3分古文単語【19~24】【55日間完成】

単元:
#国語(高校生)#古文#単語
教材:
#中高教材#古文単語330三訂版-いいずな書店#単語帳
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
19.ゆかし(3)
20.おぼつかなし(3)
21.ありがたし(2)
22.めでたし(1)
23.くちをし(1)
24.うし(1)
この動画を見る
<今日の単語>
19.ゆかし(3)
20.おぼつかなし(3)
21.ありがたし(2)
22.めでたし(1)
23.くちをし(1)
24.うし(1)
【数学】中高一貫校問題集2幾何122:円:円の接線:内接円の性質
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
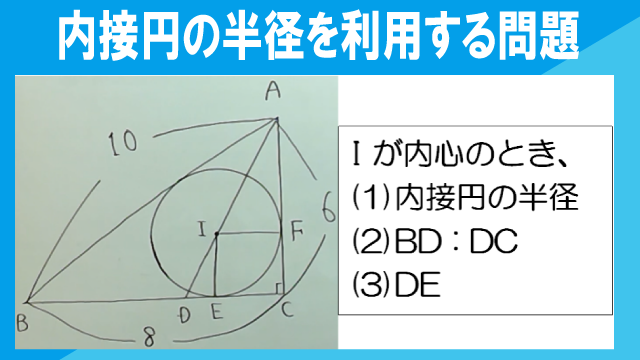
図の△ABCは、∠C=90°の直角三角形である。AB=10cm、BC=8cm、CA=6cmとし、△ABCの内接円の中心をIとする。また、直線AIと辺BCの交点をD、円ⅠとBC、CAの接点をそれぞれE、Fとする。
(1)円Iの半径を求めなさい。
(2)BD:DCを求めなさい。
(3)線分DEの長さを求めなさい。
この動画を見る
図の△ABCは、∠C=90°の直角三角形である。AB=10cm、BC=8cm、CA=6cmとし、△ABCの内接円の中心をIとする。また、直線AIと辺BCの交点をD、円ⅠとBC、CAの接点をそれぞれE、Fとする。
(1)円Iの半径を求めなさい。
(2)BD:DCを求めなさい。
(3)線分DEの長さを求めなさい。
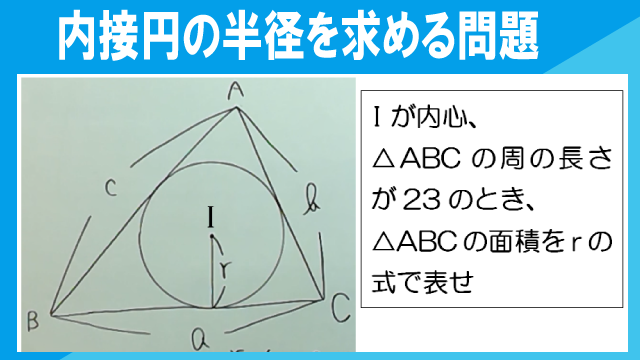
【数学】中高一貫校問題集2幾何121:円:円の接線:三角形の面積と内接円の半径
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCの周の長さが23、△ABCの内接円の半径がrのとき、△ABCの面積をrを用いて表しなさい。
この動画を見る
△ABCの周の長さが23、△ABCの内接円の半径がrのとき、△ABCの面積をrを用いて表しなさい。




